BAEKJOON : 1929, 4948, 9020, 3009

No. 1929

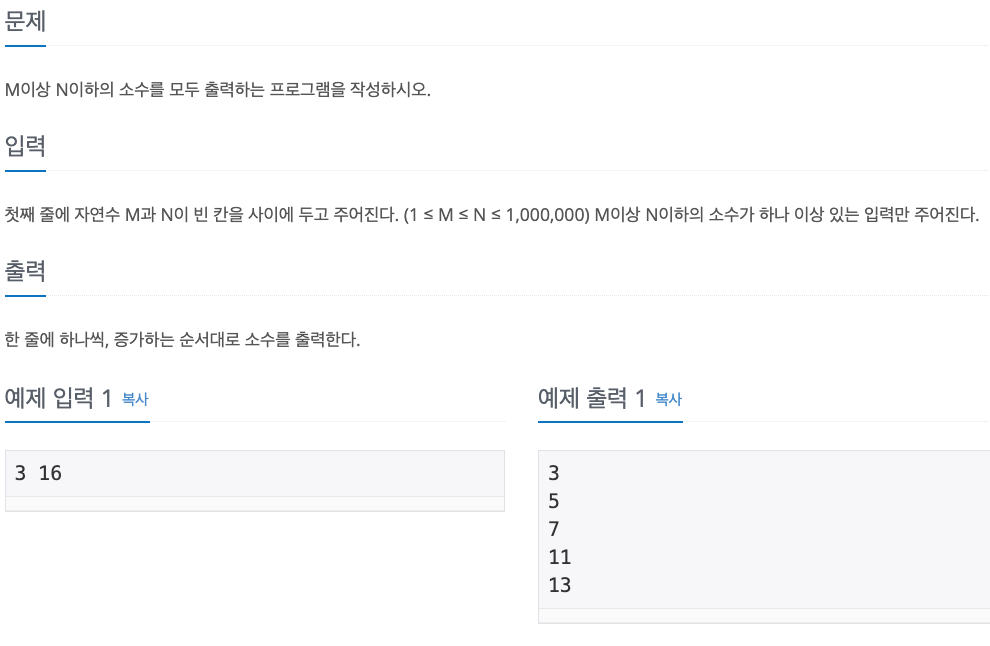
1. Problem

2. My Solution

• 모든 수에 대해서 소수인지 아닌지 판단 -> 시간초과

import sys

m,n = map(int,sys.stdin.readline().strip().split())

for num in range(m,n+1):
    if num >1:
        flag = True

        for i in range(2,num):
            if num % i == 0:
                flag = False
                break
        
        if flag == True:
            print(num)

3. Others' Solutions

• 에스토스테네스의 체 알고리즘 이용
• 모든 수에 대해서 소수인지 판단하지 않고 특정 수의 배수이면 바로 제거
• 배수를 정할 때 제곱근까지만 지정

import sys
import math

m,n = map(int,sys.stdin.readline().strip().split())
num_list = list(range(n+1))

for i in range(2, int(math.sqrt(n))+1):
    if num_list[i] == 0:
        continue
    else:
        for j in range(i+i,n+1,i):
            num_list[j] = 0


for i in range(m, n+1):
    if num_list[i] != 0 and num_list[i] > 1:
        print(num_list[i])

4. Learned

• 에라토스테네스의 체 알고리즘을 공부했다

---

No. 4948

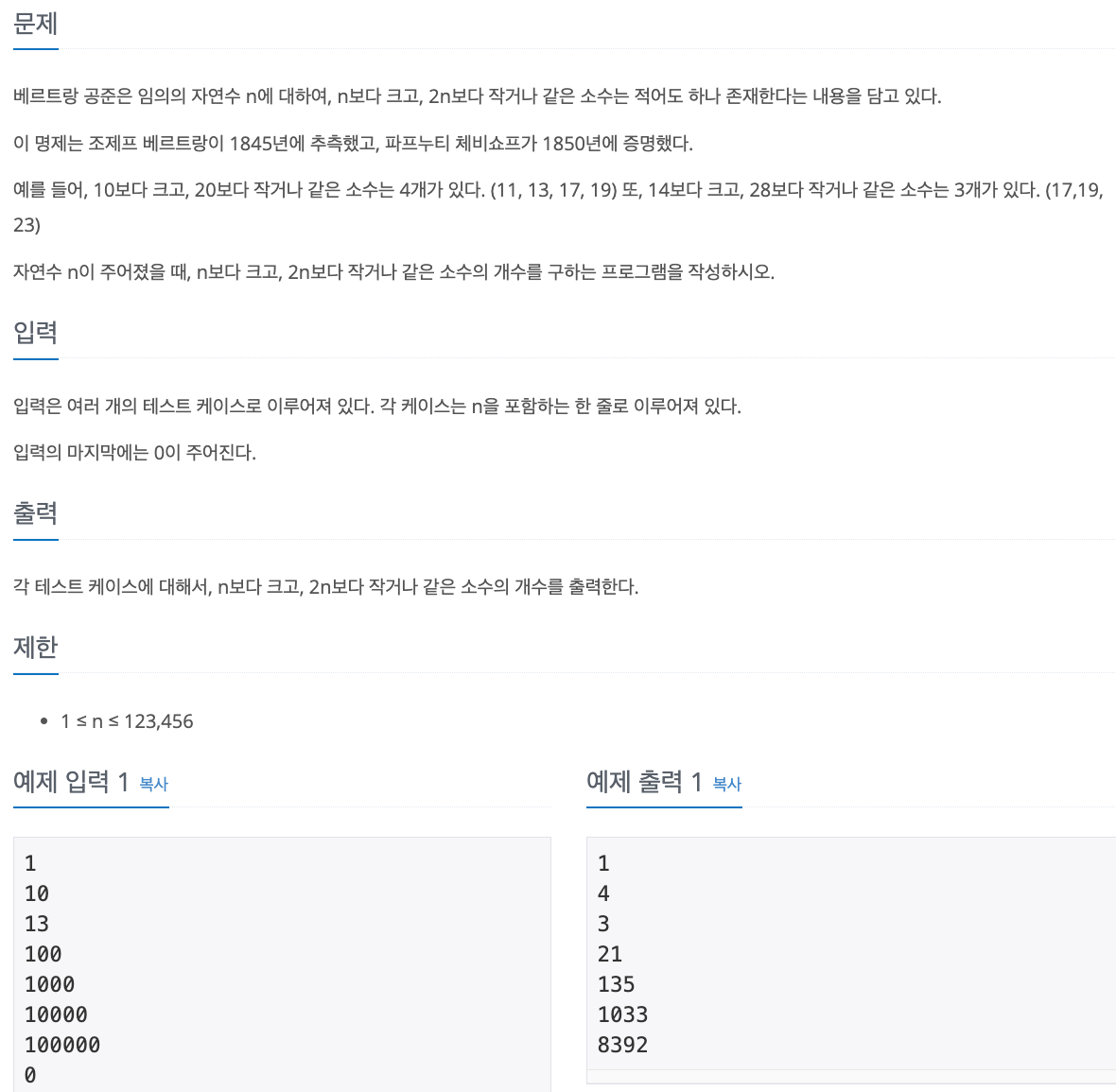
1. Problem

2. My Solution

• 2380 ms
• 각 테스트 케이스마다 prime_list 를 생성하고 소수 판단을 수행함

import sys
import math


while(True):
    
    n = int(sys.stdin.readline().strip())
    
    if n == 0:
        break

    nn = n * 2

    prime_list = [True for i in range(nn+1)]
    
    for i in range(2,int(math.sqrt(nn))+1):
        if prime_list[i] == False:
            continue
        for j in range(i+i,nn+1,i):
            prime_list[j] = False

    print(prime_list[n+1:nn+1].count(True))

3. Others' Solutions

• 123456 까지 소수를 모두 구한뒤 모든 테스트 케이스에서 사용
• 첫 테스트케이스만 시간이 오래걸리고 나머지는 훨씬 빠름
• 676 ms

import sys
import math

max_num = (123456 * 2)
prime_list = [True for i in range(max_num+1)]

for i in range(2,int(math.sqrt(max_num))+1):
        if prime_list[i] == False:
            continue
        for j in range(i+i,max_num+1,i):
            prime_list[j] = False

while(True):
    
    n = int(sys.stdin.readline().strip())
    if n == 0:
        break
    nn = n * 2

    count = 0
    for i in range(n+1, nn+1):
        if prime_list[i] == True:
            count += 1
    print(count)

4. Learned

• 각 테스트 케이스마다 공유할 수 있는 데이터가 있으면 공유하자

---

No. 9020

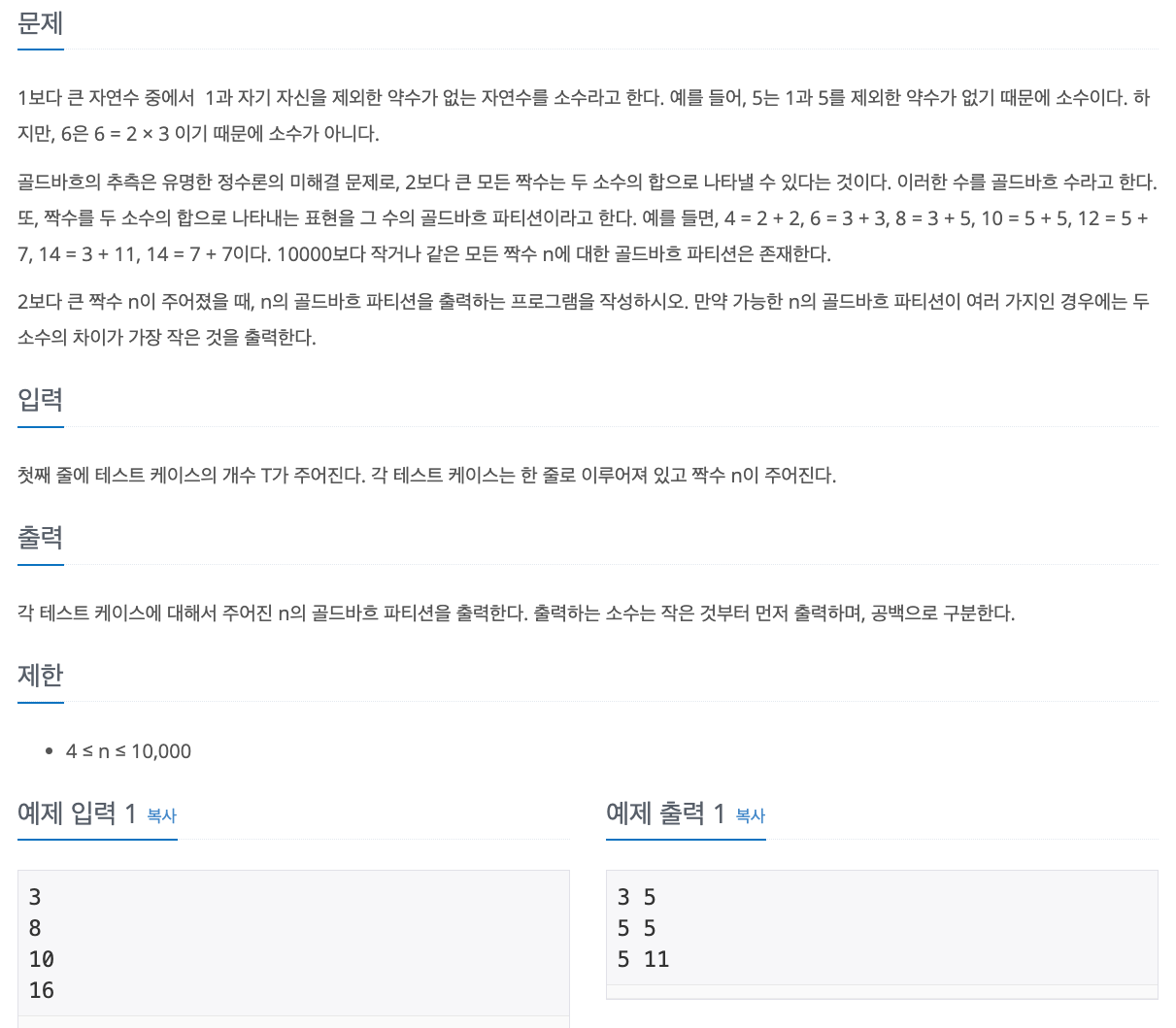
1. Problem

2. Others' Solutions

• 에라토스테네스 체 알고리즘을 이용하여 10000까지 소수 구함
• 두 소수의 차가 가장 작은 짝을 찾기 위해서 낮은 수부터 판단하지 않고 n/2 값 부터 아래로 판단
  ( 2 3 5 7 11 13 17) 존재할 때 n = 18 이면 (3,13) 보다 (5,11)을 먼저 찾아야 함
• i 값도 소수이고 n - i 값도 소수이면 둘이 합쳐서 n

import sys
import math

num_list = [True for i in range(10001)]


for i in range(2,int(math.sqrt(10000))+1):
        if num_list[i] == False:
            continue
        for j in range(i+i,10001,i):
            num_list[j] = False

test_n = int(sys.stdin.readline().strip())
    
for i in range(test_n):
    n = int(sys.stdin.readline().strip())
    
    for i in range(n//2,1,-1):
        if num_list[i] == True and num_list[n-i]==True:
            print(i, n-i)
            break

3. Learned

• range() 를 역순으로 하기 위해선 range(5,1,-1) -> [5,4,3,2]
• 한 가지 방법을 고집하지 않고 여러 방법을 시도해보자

---

No. 3009

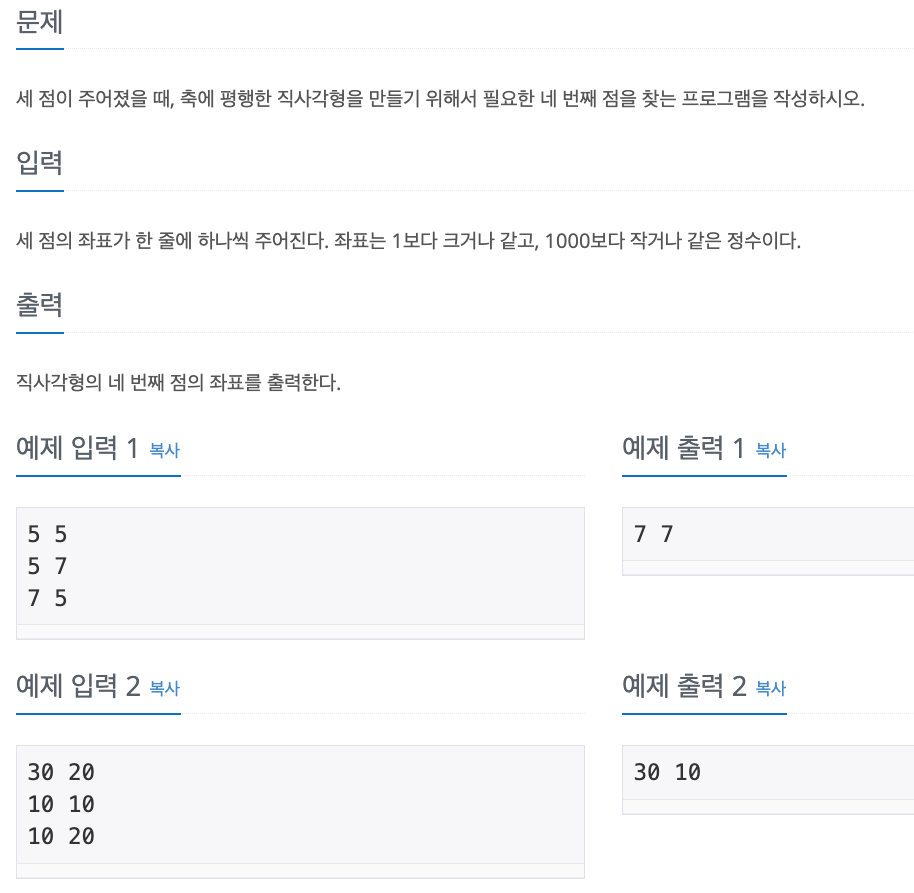
1. Problem

2. Others' Solutions

• 직사각형은 같은 값을 지닌 x 좌표, y 좌표 쌍이 2개씩 존재

import sys

x_list = []
y_list = []

for i in range(3):
    x,y = map(int,sys.stdin.readline().strip().split())

    x_list.append(x)
    y_list.append(y)

for i in range(3):
    if x_list.count(x_list[i]) == 1:
        x = x_list[i]
    if y_list.count(y_list[i]) == 1:
        y = y_list[i]

print(x,y)

3. Learned

• 문제에 소재(직사각형)가 등장한다면 해당 소재의 성질에 대해서 생각해보자