BAEKJOON : 2133, 17404

No. 2133

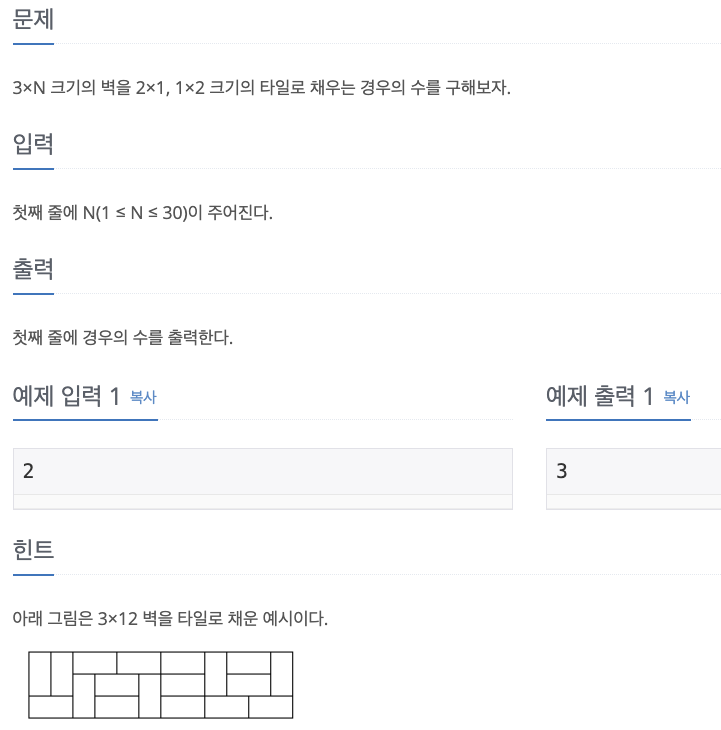
1. Problem

2. Others' Solutions

• n 이 홀수일 때는 타일을 채울 수 없음
• 타일이 끝나는 경우의 수(모양)를 생각해야 함
  - 3 x 2 일때, 3가지 (고정)
  - 3 x 4 일때, 5가지
  - 3 x 6 일때, 7가지 ... 이렇게 힌트에 나온 것 처럼 특이한 경우가 2가지씩 추가됨

import sys

n = int(sys.stdin.readline().rstrip())
dp = [0] * 31
dp[2] = 3

for i in range(4,31):
    if i % 2 == 0:
        dp[i] += dp[i-2]*3		# 고정된 3가지의 모양
        for j in range(i-4,0,-2):
            dp[i] += dp[j] * 2		# 지금까지 나타난 특이한 모양
        dp[i] += 2			# 추가적으로 생겨난 특이한 모양
    
print(dp[n])

3. Learned

• 힌트를 잘 살펴보자
• 규칙이 n이 커지면서 계속 유지되는지 아니면 추가적인 규칙이 나타나는지 확실히 판단하자
  
  

---

No. 17404

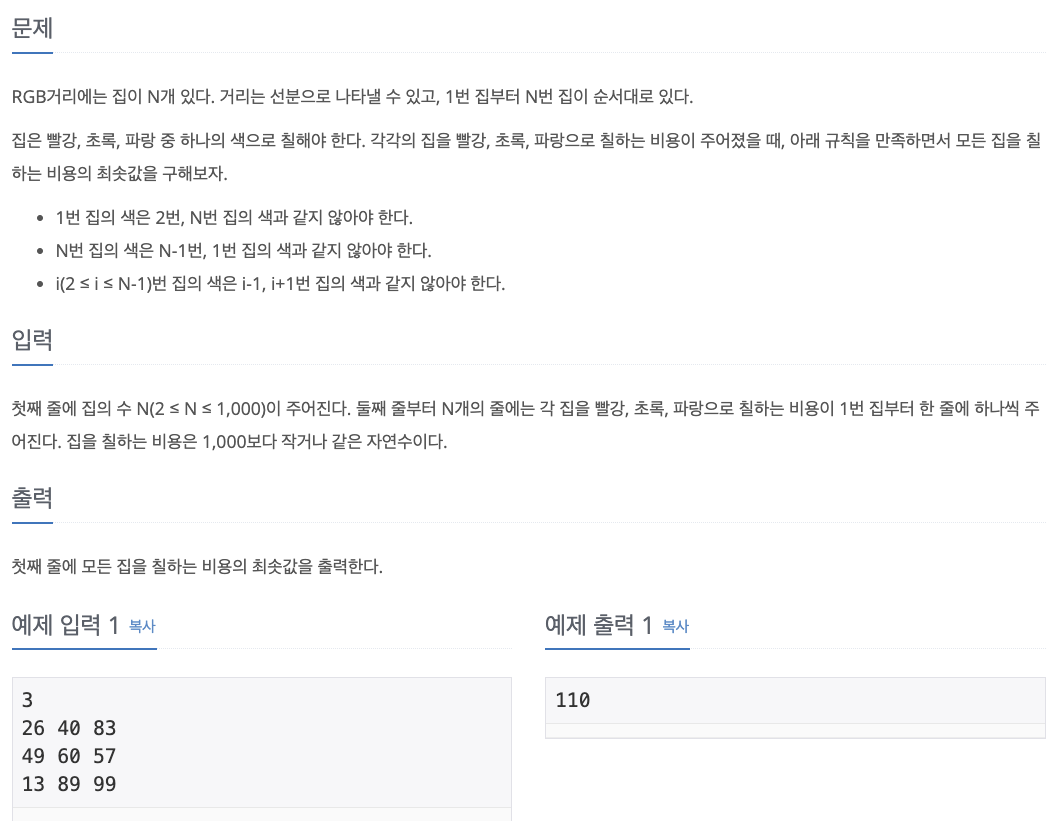
1. Problem

2. Others' Solutions

• RGB 거리 문제 응용
• 첫 번째 집이 어떤 color 로 칠해졌는지 정보를 계속 가지고 있기에는 복잡함
• 첫 번째 집의 색을 고정한 뒤 모든 경우의 수를 구함 (마지막에 첫 번째 집의 색과 동일한 경우만 제외)

import sys
import math

n = int(sys.stdin.readline().rstrip())
dp = [[0,0,0] for _ in range(n)]
color = []
result = math.inf

for i in range(n):                      # 집 마다 RGB color 값 입력 받음
    color.append(list(map(int,sys.stdin.readline().rstrip().split())))

for i in range(3):

    for j in range(3):                  # 첫 번째 집에서 R,G,B 중에 하나를 택하고 나머지는 inf 값으로 선택되지 않게 설정
        if i == j:
            dp[0][j] = color[0][j]
        else:
            dp[0][j] = math.inf
    
    for k in range(1,n):                # RGB 거리 문제와 동일하게 dp를 이용하여 최솟값 도출
        dp[k][0] = min(dp[k-1][1] + color[k][0], dp[k-1][2] + color[k][0])
        dp[k][1] = min(dp[k-1][0] + color[k][1], dp[k-1][2] + color[k][1])
        dp[k][2] = min(dp[k-1][0] + color[k][2], dp[k-1][1] + color[k][2])

    for j in range(3):                  # 첫 번째 집과 색이 같은 경우를 제외한 결과중에 min 값 결정
        if i == j:
            continue
        else:
            result = min(result, dp[n-1][j])

print(result)

3. Learned

• 초기에 특정 정보를 계속 가지고 있기 어려우면, 특정 경우의 수로만 나올 수 있는 값들만을 구하자
• 최댓값, 최솟값 문제 중에서 여러 선택지가 있을 때 한가지만을 고르도록 하기 위해서 나머지를 -inf 또는 inf 로 설정할 수 있음