Big O (1) : O, O(n), O(n^2)

📚 Big O

💡 Big O는 컴퓨터 알고리즘에서 매우 중요한 개념으로, 두 개의 코드를 비교하는 방법론이다.

• 예를 들어, 같은 역할을 수행하는 더 읽기 쉬운 코드1 과 더 간결하고 코드 수가적은 코드2가 있는데, Big O는 이러한 코드들을 수학적으로 얼마나 효율적으로 실행되는지를 비교하는 방법이다.

💡 시간복잡도 : 측정가능한 정도

• 이때 시간 복잡도는 시간으로 측정되지 않는다. 대신 무언가를 완료하는 데 필요한 작업 횟수로 측정된다.

💡 공간복잡도

• 해당 코드들에 소요시간 보단, 해당 코드들이 작동하면서 차지하는 메모리상에 공간에 대해 더 높은 우선순위를 두는 것.

📚 Big O - Worst Case

• 💡 시간복잡도와 공간복잡도를 다룰 때, 주로 만나게 되는 그리스 문자가 있다.
• Big O는 프로그래밍의 있어 최악의 경우를 다루는 표기법이다.
  • 즉 Big O 에는 최악의 경우만 있고, 최선의 경우나 보통의 경우는 고려하지 않는다.

ex) 만약, 1-7 로 된 배열에서 숫자를 찾을 경우...
최고의 경우는 0번 인덱스를 찾는 경우이고, 최악의 경우는 6번 인덱스이다.
그리고 평균적인 경우는 3번 인덱스를 찾는 경우이다.

• Ω(오메가) : 최고의 경우
• θ(세타) : 평균적인 경우
• Ο(오미크론 - o로도 더 잘 알려져 있음) : 최악의 경우

📚 Big O(n)

💡 O(n)은?

• O(n)은 알고리즘의 실행 시간이 입력 크기(n)에 직접 비례할 때 사용되는 표현
• '직접 비례(proportional)'란, 입력 크기가 2배로 증가하면 실행 시간도 대략 2배로 증가한다는 뜻
• O(n)은 선형 시간 복잡도(linear time complexity)를 나타낸다.

💡 중요한 점,

• O(n)이 선형적인 관계를 나타낸다는 것이지, 실행 시간이 항상 n과 정확히 동일하다는 것을 의미하지는 않는다는 점이다.
• 예를 들어, 알고리즘이 n개의 입력에 대해 2n번의 연산을 수행한다고 해도, 이는 여전히 O(n)으로 분류된다.
• 왜냐하면, 큰 관점에서 보면 실행 시간이 입력 크기에 비례하기 때문이다.

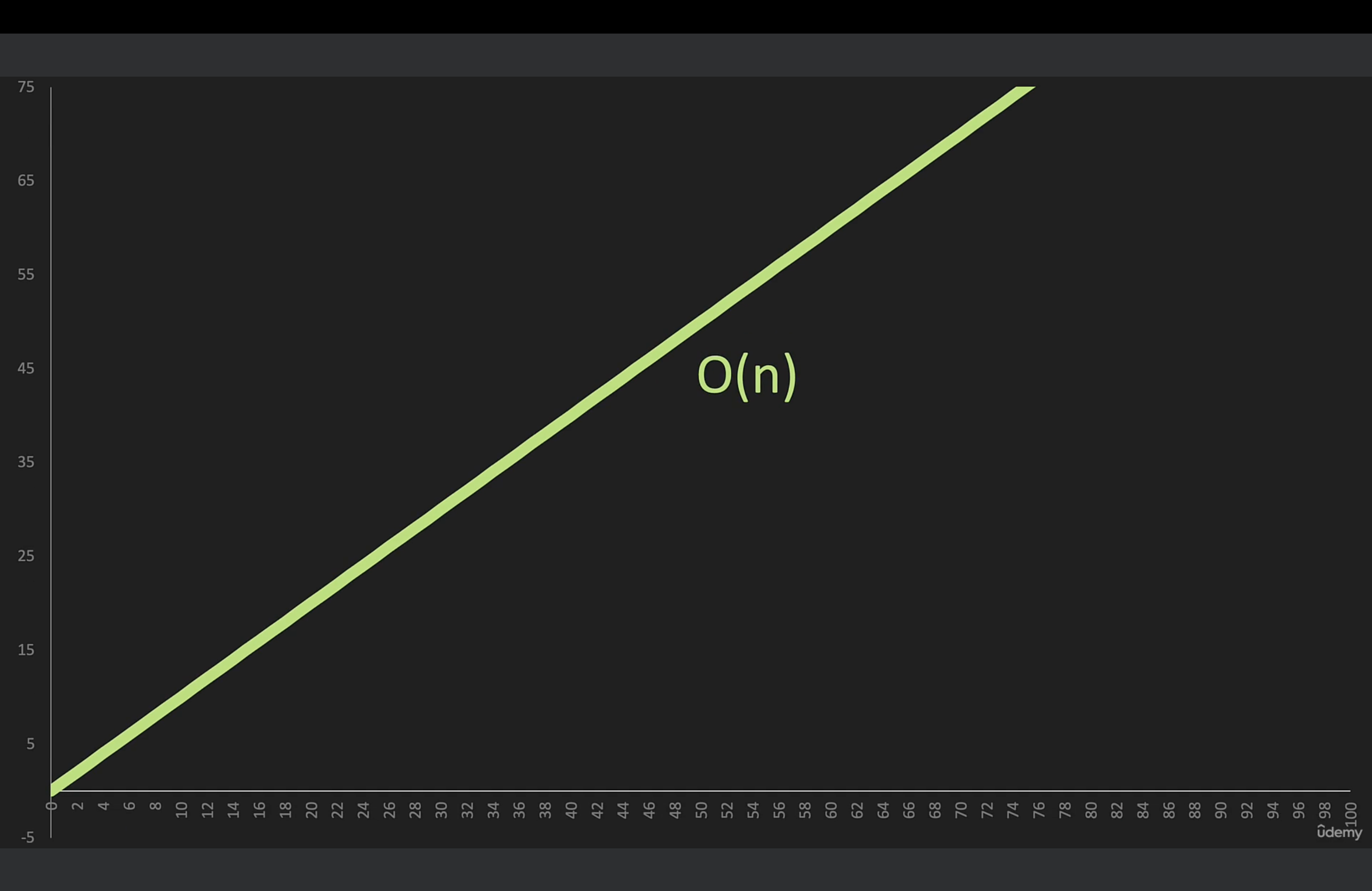
• ex) O(n) 코드 예시 + 그래프

def print_items(n) :
	for i in range(n) :
    	print(i)

• 💡 그래프에서 보이는 바와 같이, O(n)의 그래프는 직선을 그린다.
  • 이 직선의 기울기는 알고리즘이 입력에 대해 수행하는 연산의 '비율'을 나타낸다.
  • 하지만 모든 O(n) 알고리즘이 동일한 기울기를 가지는 것은 아니며, 기울기는 알고리즘의 특정 구현에 따라 달라질 수 있다.
  • 중요한 것은, n이 커짐에 따라 실행 시간이 선형적으로 증가한다는 점이다.

📚 Drop Constants

💡 Drop Constants은 Big O 표기법을 단순화할 수 있는 방법 중 하나.

def print_items(n) :
	for i in range(n) :
    	print(i)
       
	for j in range(n) :
    	print(j)    

• 위 코드는 똑같은 작업을 두 번 반복한다. 즉 n + n = 2n번 반복되는 코드지만 표기할 때는 O(2n)이 아니라 O(n)으로 작성한다. 이를 Drop Constants 라고 한다.

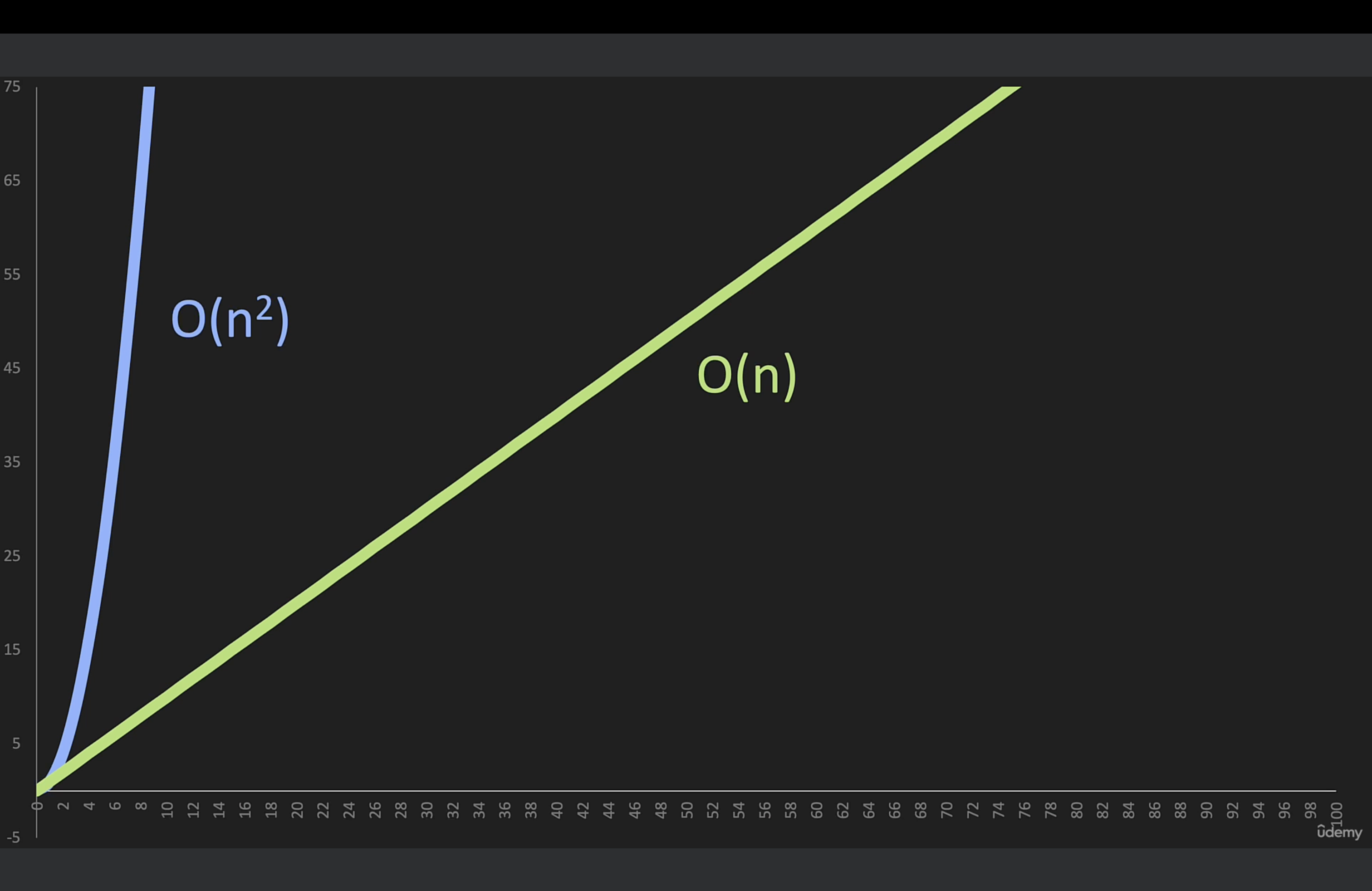
📚 Big O(n^2)

def print_items(n) :
	for i in range(n) :
    	for j in range(n) :
            print(i, j)    

• 해당 코드를 출력해보면, 총 100번 즉 n * n 번 출력된다. 이는 O(n^2) 이다.
  

📚 Drop Non-Dominants

💡 Drop Non-Dominants는 Big O 표기법을 단순화할 수 있는 방법 중 하나.

def print_items(n):
	for i in range(n) :
    	for i in range(n) :
        	print(i, j)
           
	for k in range(n) :
    	print(k)

• 이 코드는 O(n^2), O(n)에 프로그래밍이 중첩되었다. 즉 출력된 항목의 총합은 O(n^2 + n) 이다.

• O(n^2 + n) 같은 경우, n 이 유의미하게 커질 경우 n은 무시해도 좋은 정도이기에, O(n^2 + n)은 O(n^2) 으로 표시한다.

🗣️ (n^2) : dominant term, n : undominant term