Big O (2) : O(1), O(log n), O(nlog n)

📚 Big O(1)

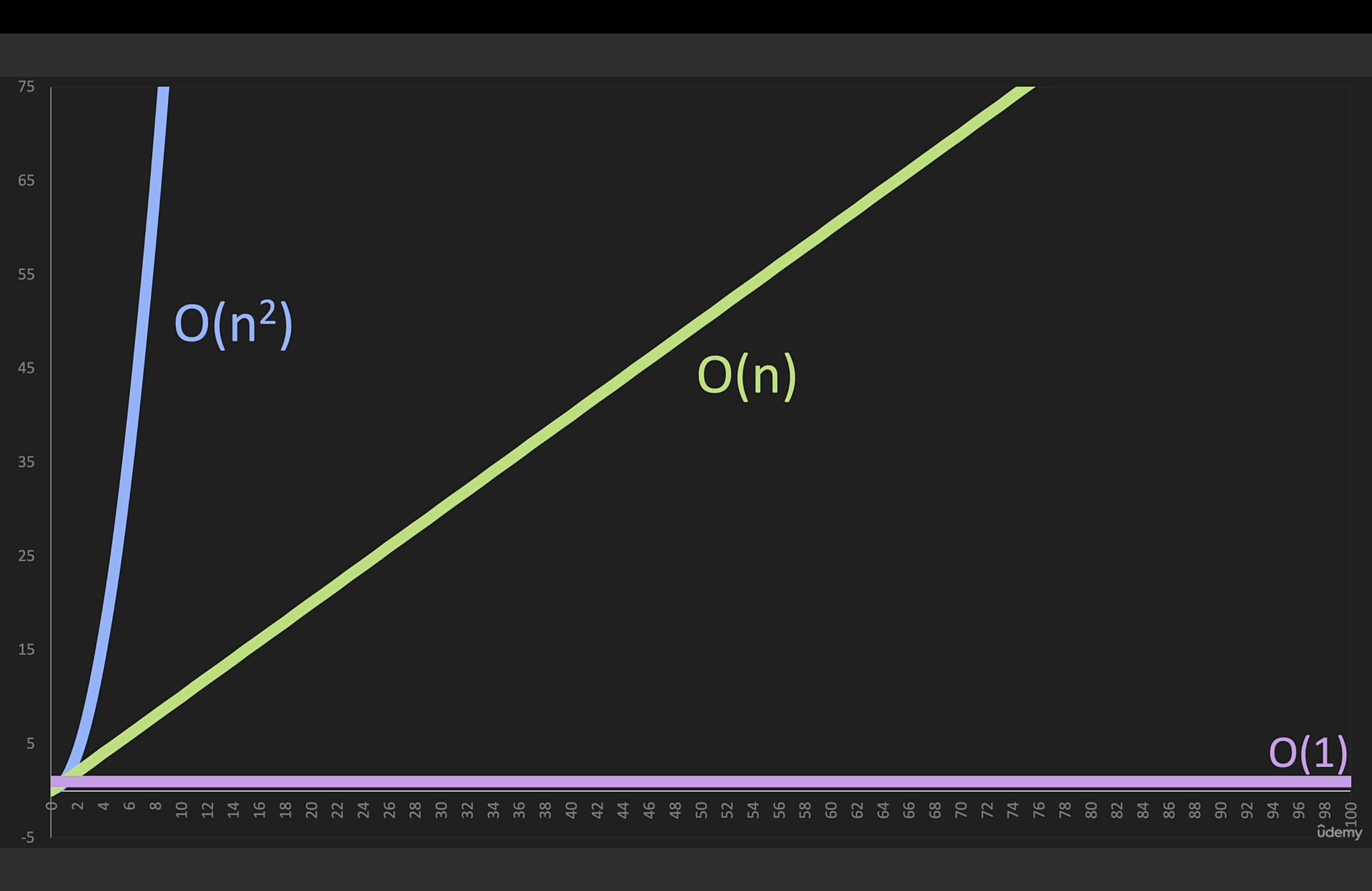
💡 O(n), O(n^2)은 n이 커지면 O가 증가한다. 하지만 O(1)은 추가만 하는 경우이다.
💡 O(1)은 constant 시간이라고도 한다. 그 말은 n이 증가해도 작업수는 항상 일정함을 뜻한다.

🗣️ 가장 효율적인 빅 O

def add_items(n) 
	return n + n

• 이 같은 함수에서는 n이 아무리 커져도 실행 횟수는 1회 이다.
  

📚 Big O(log n)

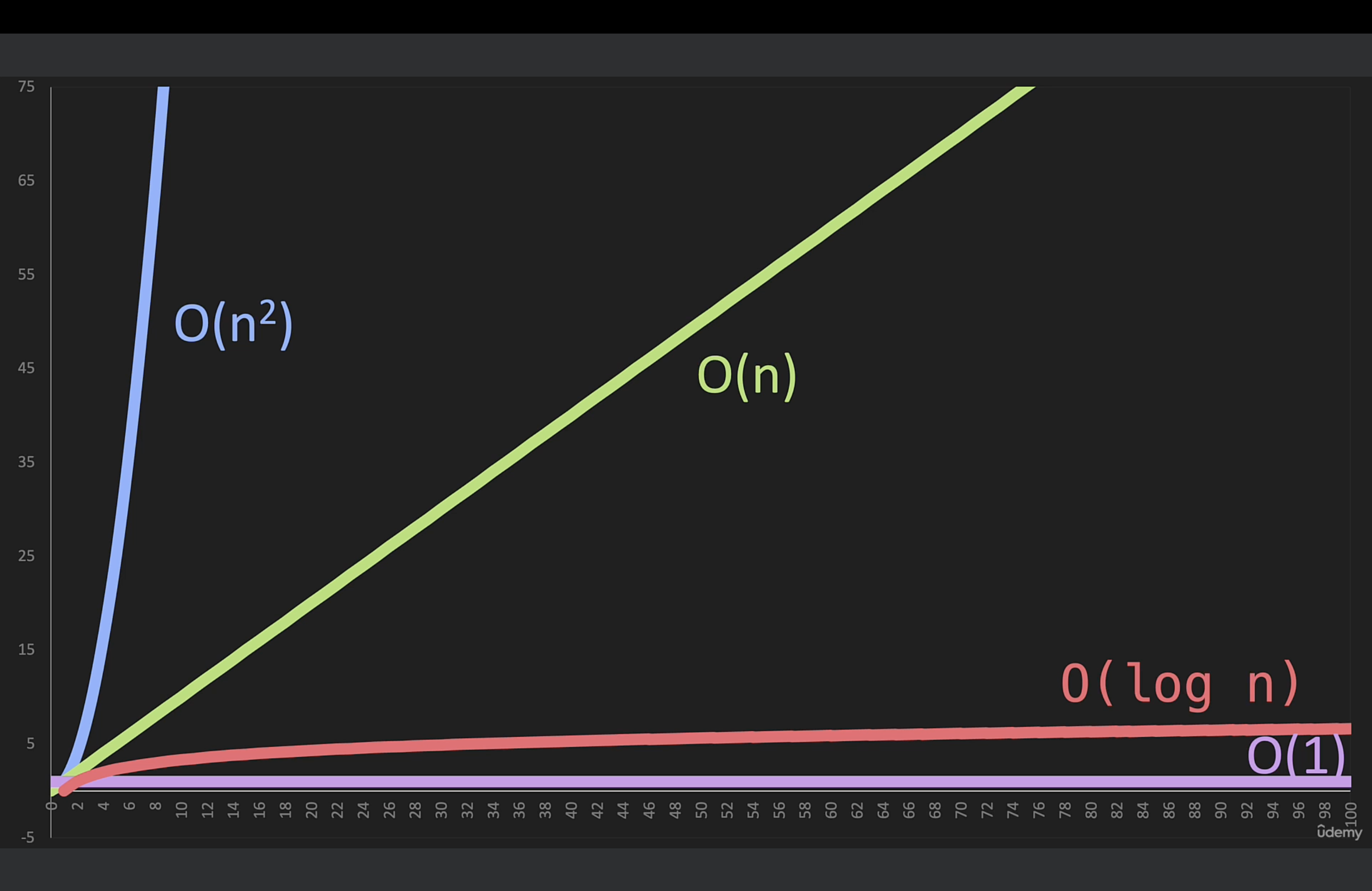
💡 O(log n)은 O(1) 만큰 효율적이지 않지만 O(n), O(n^2) 보다는 훨씬 효율적이다.

💡 1 - 8까지 정렬된 배열이 있다라고 가정했을 때, 여기에서 가장 효율적으로 숫자 1을 찾는 방법은?

• 배열을 반으로 나눈다, [1-4], [5-8] 우리가 원하는 숫자1은 첫번째 배열에 있으므로, [1-4]만 갖고 나머지는 버린다.
• 위와 같이 반으로 나누고 필요한 숫자만 찾는 작업을 우리가 원하는 숫자가 나올 때 까지 반복한다.
• 1 - 8까지 정렬된 배열에 경우 3회 반복하면 값을 찾을 수 있다.
• 이거를 수학적으로 나타내면, 밑이 2인 log8 = 3 으로 표시할 수 있다.
  

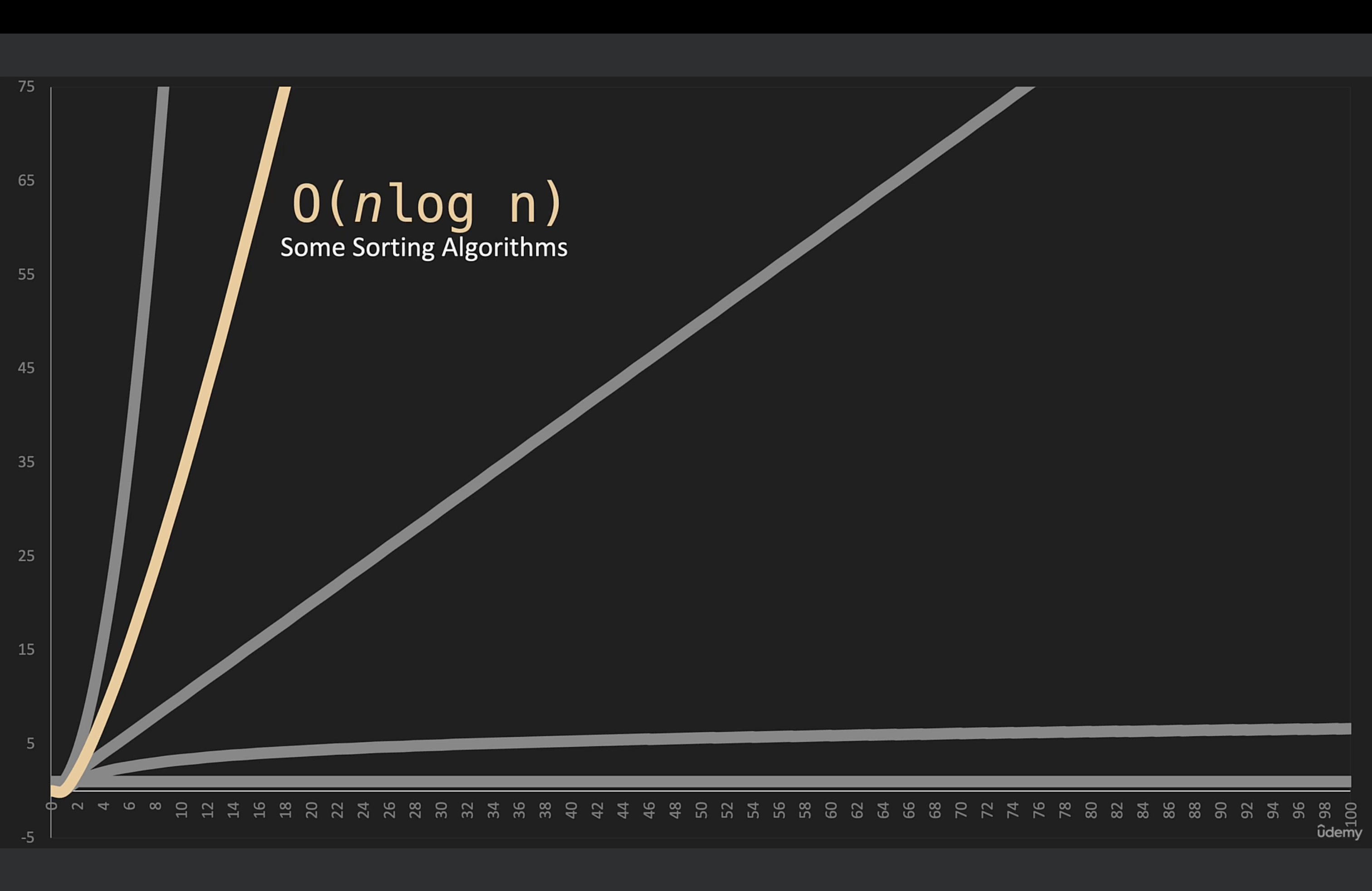
📚 Big O(nlog n)

💡 n log n 은 일부 정렬 알고리즘과 함께 사용된다.(병합정렬, 퀵정렬)
💡 가장 효울적으로 분류 알고리즘을 만드는 방법이다.
💡 n log n을 통해 숫자뿐 아니라 다양한 유형의 데이터를 정렬 할 수 있다.