NP문제(문제의 종류, NP-hard, P-NP문제)

📚 1. 문제의 종류

💡 문제의 종류를 알아야 하는 이유

• 어떤 문제가 다항식 시간안에 해결될 수 없다는 것을 안다면, 최적의 알고리즘을 찾느라 노력을 들이는 대신 대안이 될 수 있는 근사 알고리즘을 사용함으로써 노력을 허비하는 것을 막을 수 있음

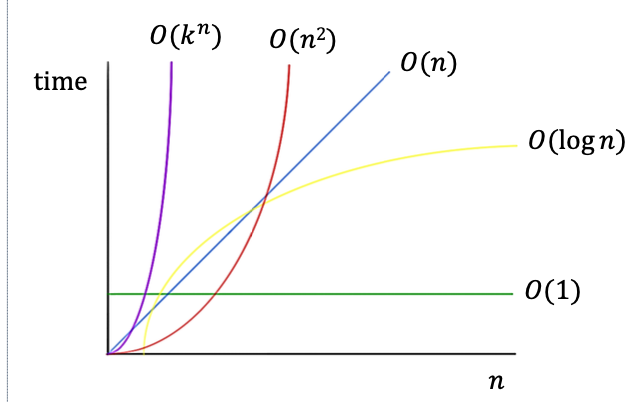
💡 시간의 종류

• 상수(costant)시간 : O(1)
• 다항식(polynomial)시간 : O(n^k)
• 지수(exponential)시간 : O(k^n)
• 계승(factorial)시간 : O(n!)
• Tractable / Intractable
  • Tractable : 문제의 해결이 현실적인 시간, 즉 다항식 시간안에 끝나는 경우
  • Intractable : 입력의 크기인 n이 커질 때 현실적인 시간내에 끝나지 않는 경우(O(k^n),O(n!)인 경우)

📚 2. NP-hard

💡 P문제와 NP문제

• P(polynomial time)문제 : tractable한 문제 즉 다항식 시간 안에 답을 구할 수 있는 문제, (ex: 비교정렬)
• NP(nondeterministic polynomial time)문제 : 답이 주어졌을 때 그것이 정답인지를 다항식 시간 안에 확인할 수 잇는 문제 ( ex: 모든 P문제 )

💡 문제의 변환

• 어떤 문제 A를 다른 문제 B로 다음의 조건을 만족하면서 변환하는 것을 다항식 시간 변환이라고 하고 (𝐴 ≤𝑝 𝐵) 와 같이 표기.
  • 변환을 완료하는데 다항식 시간이 소요된다.
  • B의 답을 이용하면 A의 답을 구할 수 있다.

💡 NP-hard의 정의

• 모든 NP 문제 Q에 대해 (𝑄 ≤𝑝 𝐴)
• 하나의 NP-hard 문제를 다항식 시간 안에 풀 수 있으면 모든 NP문제를 다항식 시간 안에 풀 수 있음.
  • 지금까지는 어떤 NP-hard 문제도 다항식 시간 안에 풀 수 있는 알고리즘이 발견되지 않음.
  • 현재로서는 NP-hard 문제들은 Intractable.
• 다음 조건을 만족하는 문제 A에 대해 NP-hard이다. (𝑄 ≤𝑝 𝐴)
• A의 답을 이용하면 Q의 답을 구할 수 있지만 역은 성립하지 않음, 따라서 A는 Q보다 어려운 문제라고 할 수 있고, NP-hard문제는 모든 NP 문제보다 어려운 문제이므로 가장 어려운 문제들의 집합이라고 할 수 있음.
• 다음 조건을 만족하는 문제 A는 NP-hard이다. (이미 알려진 NP-hard문제 Q에 대해 (𝑄 ≤𝑝 𝐴))

💡 SAT(satisfiability)문제

• 부울식 만족 문제 : 주어진 boolean expression(부울식)을 참으로 만드는 값이 존재하는가?

💡 NP-complete의 정의

• 다음 두 조건을 동시에 만족하는 문제 A는 NP-complete 문제이다.
  • A는 NP이다.
  • A는 NP-hard이다.
• NP-complete은 NP-hard에 속하기 때문에 NP-complete인 문제를 NP-hard라고 말해도 올바른 표현이고 보통 NP-hard라는 표현을 많이 사용.

💡 해밀토니안 싸이클 문제

• (HAM-CYCLE) 무방향(undirected) 그래프𝐺 = (𝑉, 𝐸)에 해밀토니안 싸이클이 존재하는가?
  • 해밀토니안(Hamiltonian) 싸이클: 모든 정점을 한 번씩만 방문하고 돌아오는 경로
  • NP-hard 문제

💡 TSP 문제

• (TSP) 양의 가중치를 갖는 무방향 완전 그래프(모든 정점 사이에 간선이 존재하는 그래프) 𝐺 = (𝑉, 𝐸)에 길이 𝐾 이하인 해밀토니안 싸이클이 존재하는가?
• TSP 문제의 NP-complete 여부
  • NP 여부와NP-hard 여부를확인해야함
  • NP:싸이클이 주어지면 길이가 𝐾이하의 해밀토니안 싸이클 인지 확인 하는 것(가중치의 합을 계산해서 𝐾와 비교 하는 것)은 다항식 시간 안에 가능
• TSP 문제의 NP-complete 여부
  • NP-hard: 𝐻𝐴𝑀_𝐶𝑌𝐶𝐿𝐸 ≤𝑝 𝑇𝑆𝑃
  • 해밀토니안싸이클이존재하는가? → 길이가 𝑉 이하인해밀토니안싸이클이존재하는가?
  • NP이고, 𝐻𝐴𝑀_𝐶𝑌𝐶𝐿𝐸 ≤𝑝 𝑇𝑆𝑃로 인해 NP-hard이므로 TSP 문제는 NP-complete.

💡 결정 문제와 최적화 문제

• 결정(decision) 문제
  • 어떤 입력(input)에 대해 답이 예/아니오 중 하나인 문제
  • 양의 가중치를 갖는 무방향 완전 그래프 𝐺 = (𝑉, 𝐸)에 길이𝐾 이하인 해밀토니안 싸이클이 존재 하는가?
• 최적화 문제
  • 어떤 입력에 대해 최적의 답을 찾아야 하는 문제
  • 양의 가중치를 갖는 무방향 완전 그래프 𝐺 = (𝑉, 𝐸)에서 가장 짧은 해밀토니안 싸이클은?

💡 최적화 TSP 문제의 NP-hard 여부

• 𝑇𝑆𝑃𝐷𝐸𝐶𝐼𝑆𝐼𝑂𝑁 ≤𝑝 𝑇𝑆𝑃𝑂𝑃𝑇𝐼𝑀𝐼𝑍𝐴𝑇𝐼𝑂𝑁
  • 다항식 시간 안에 문제 변환이 가능 한지?
  • 결정 TSP와 최적화 TSP는 똑같은 그래프를 사용 하면 되기 때문에 변환이 필요 없음
• 최적화 TSP 문제의 답을 이용 해서 결정TSP 문제의 답을 구할 수 있는지?
  • 가장 짧은 해밀토니안 싸이클의 길이를 구했 다면, 주어진𝐾 이하의 해밀토니안 싸이클이 존재 하는지에 대해 예/아니오를 답할 수 있음.

💡 최적화 TSP 문제의 NP-complete 여부

• 어떤 해밀토니안 싸이클이 주어졌을 때 그것이 가장 짧은 해밀토니안 싸이클인지를 다항식 시간 안에 확인할 수 있을까? → No
• 최적화 TSP 문제는 NP-hard 문제이지만 NP 문제는 아니기 때문에 NP-complete 문제가 아님

📚 3. P-NP 문제

💡 P-NP 문제

• 주어진 답을 다항식 시간에 정답인지 확인할 수 있는 문제(NP 문제)는
  다항식 시간에 답을 구할 수 있는 문제(P 문제)일까?
  class NP = class P?
  NP = P이면 모든 NP-complete 문제들을 다항식 시간 안에 해결 할 수 있음
  지금까지 NP-complete 문제들을 다항식 시간 안에 풀수 있는 알고리즘이 발견 된 적은 없음
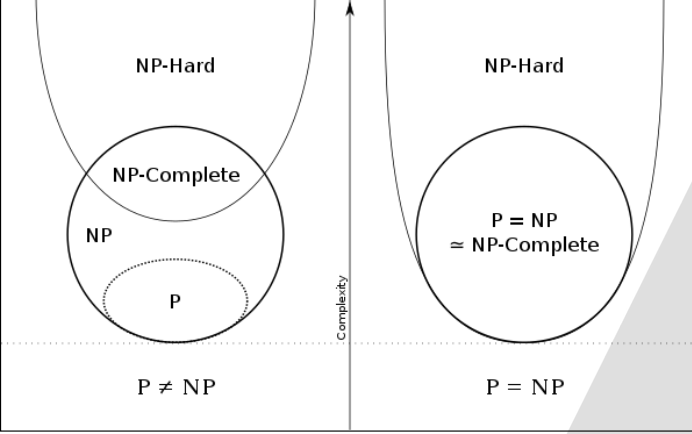
  NP ≠ P라고 추정 하고 있지만, NP = P와NP ≠ P 둘다 증명된 바가 없음

💡 P, NP, NP-hard, NP-complete의 관계