그래프3: (TSP, 분기한정 탐색, A*탐색 알고리즘, 몬테카를로 트리 탐색)

📚 1. TSP

💡 TSP 문제란?

• Travelling Saleman Problem
• 해밀토니안 싸이클 : 그래프의 모든 정점을 방문하고 돌아오는 싸이클
• TSP는 가장 짧은 헤밀토니안 싸이클을 찾는 문제
• 다음과 같은 그래프에 각 정점들이 도시가 되고, 한 세일즈맨이 각 도시들을 여행하고 돌아올 때, 최적의 경로를 찾기 위한 문제 해결법

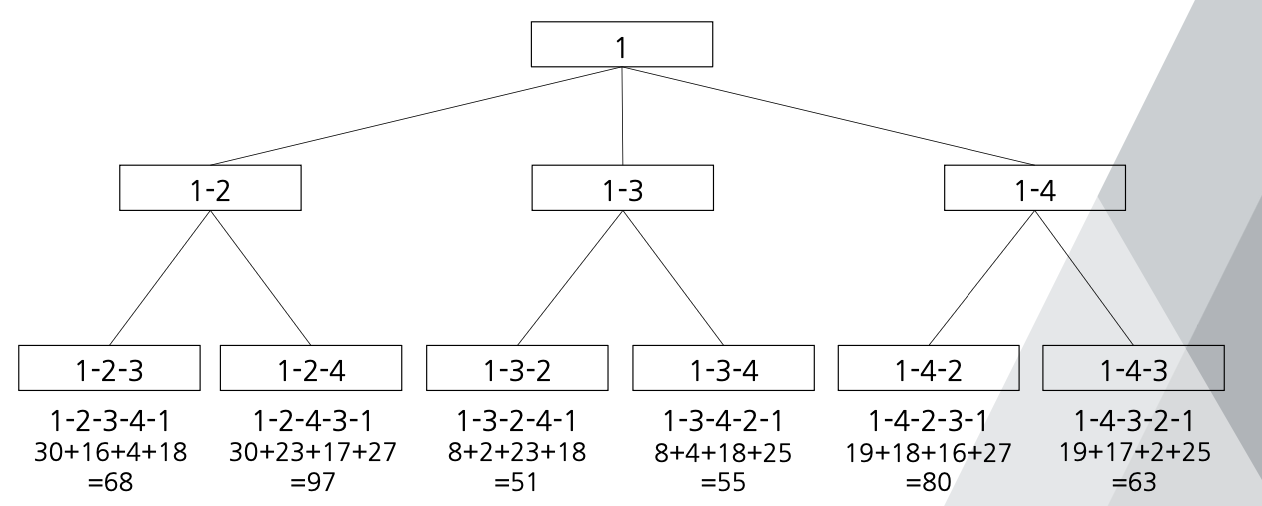
💡 상태공간 트리

• 문제풀이 과정에서 해의 상태를 노드로 나타낸 트리

💡 사전식 탐색

• 모든 경우의 수를 탐색하는 것
• 탐색해야 하는 수가 커지면 모든 경우의 수를 탐색하는 것은 매우 오랜 시간이 소요됨
• 탐색을 효율적으로 수행해야 함

📚 2. 분기한정 탐색

💡 분기한정 탐색

• 특정 분기로 진행해도 기존 최적해보다 나은 해를 찾을 수 없다고 판단될 때 되돌아가 다른 상태를 탐색
• 백트래킹 : 탐색을 하다 더 진행하기 어려울 때 되돌아가 다른 길을 탐색하는 것 : 일반적으로 깊이우선탐색을 이용하여 구현됨
• 분기한정 탐색의 조건
  • 탐색을 위한 모든 경우의 수를 나열할 수 있어야 함.
  • 가지치기(특정 분기를 더 이상 진행하지 않겠다고 결정하는 것)를 위한 기준이 존재해야 함.
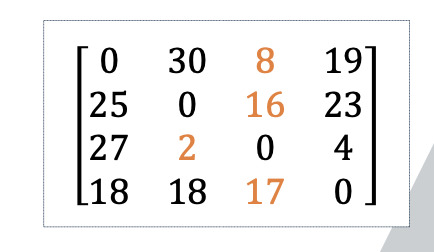
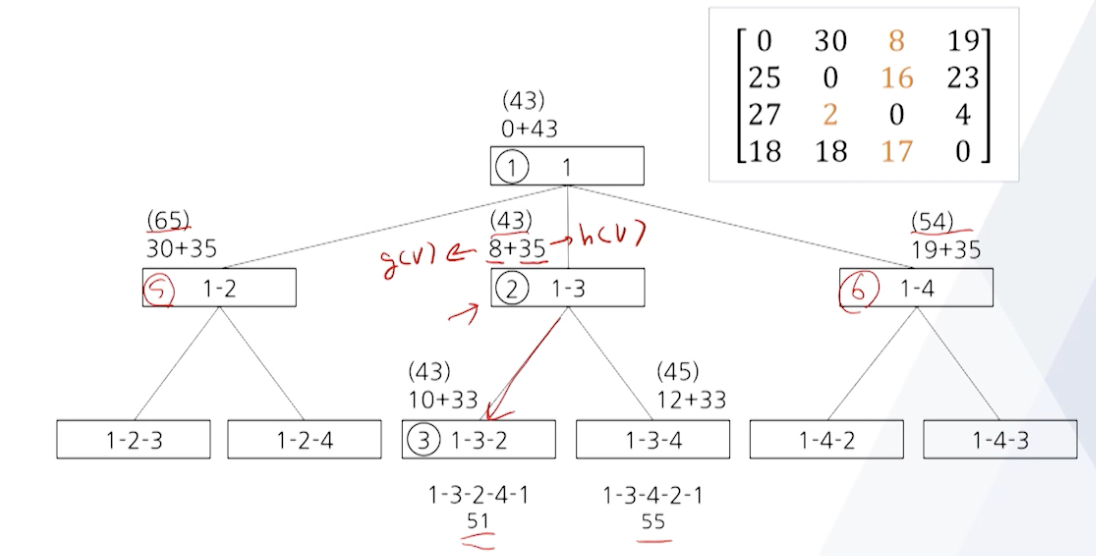
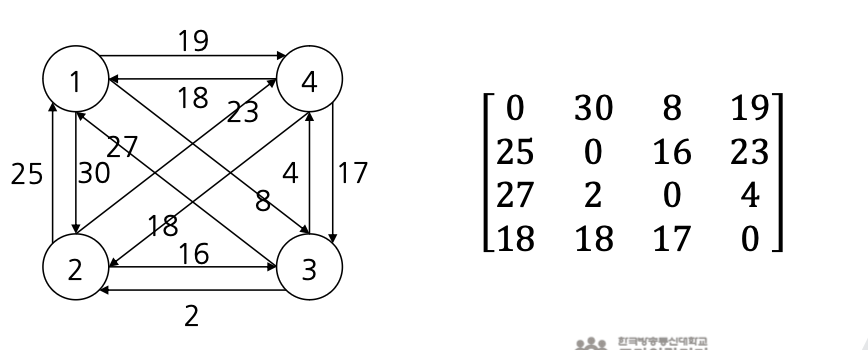
• 분기한정 탐색의 예
  • 
  • 정점 1 : 30, 8, 19 (최솟값 : 8)
  • 정점 2 : 25, 16, 23 (최솟값 : 16)
  • 정점 3 : 27, 2, 4 (최솟값 : 2)
  • 정점 4 : 18, 18, 17 (최솟값 : 17)
  • 해밀토니안 싸이클 길이의 하한 값 : 8 + 16 + 2 + 17 = 43

💡 병령 컴퓨팅을 이용한 분기한정 탐색

• 1 : 기존에 알려진 해를 기준해로 기록
• 2 : 컴퓨터들이 상태곤간 트리의 각각 다른 부분트리를 맡아서 탐색하되 기준해 값을 사용하여 분기한정 탐색을 진행
• 3 : 기준해보다 좋은 해를 발견하게 되면 기준해를 갱신하고 다른 컴퓨터가 사용할 수 있도록 전파

📚 3. A* 탐색 알고리즘

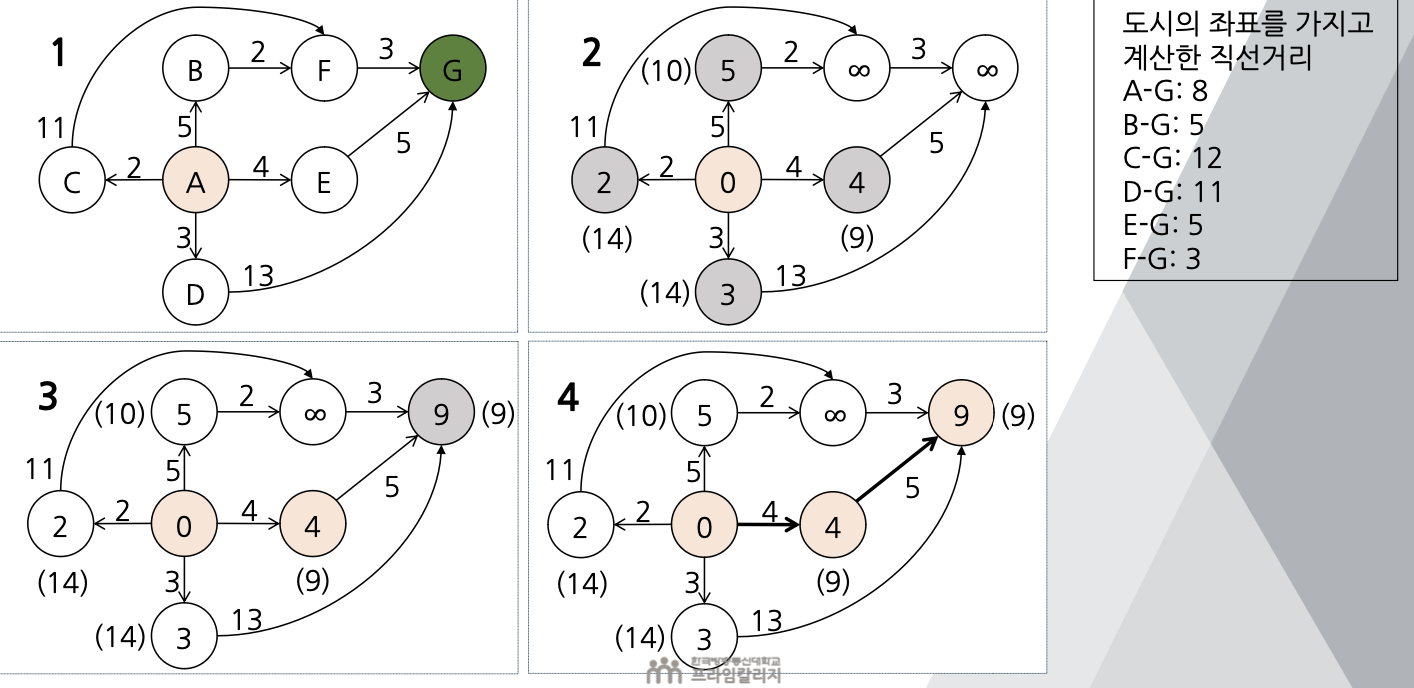
💡 다익스트라 알고리즘의 문제

• 시작 정점부터 모든 정점까지의 최단경로를 구하기 때문에 특정 도착 정점 까지의 최단경로만 구하려고 할 때 낭비가 많음.
  • 다익스트라 알고리즘으로 특정 도착 정점까지의 최단경로를 구할 때는 그 정점까지의 최단경로가 발견되면 탐색을 중단.

💡 A* 탐색 알고리즘

• 상태공간트리를 좀 더 효율적으로 탐색하기 위한 알고리즘
• 그래프의 시작 정점에서 도착 정점까지의 최단경로를 구하는 알고리즘
  • 시작 정점에서 현재 정점 v까지의 경로의 길리 g(v)와 현재 정점 v에서 도착 정점까지의 추정 잔여거리 h(v)를 동시에 고려하는 방법(매 단계에서 g(v) + h(v)가 최소인 정점을 선택)
• 네비게이션, 게임 상에서의 길찾기 등에 응용됨.
• 그래프/상태공간 트리에서 기존에 발생한 비용 뿐만 아니라 향후에 발생할 추정 비용을 같이 고려하는 방법

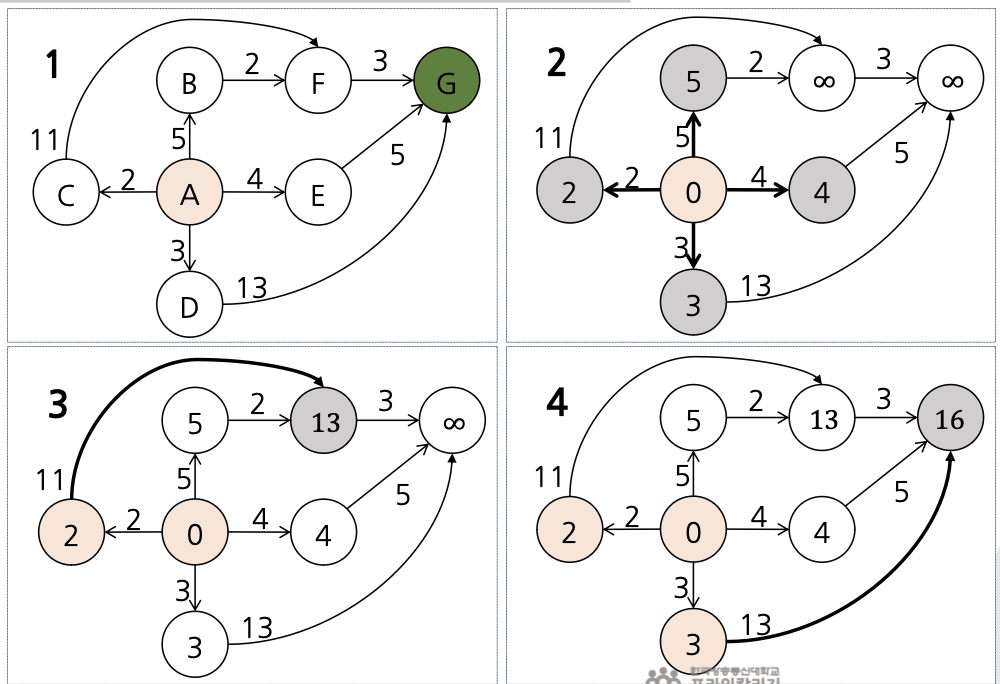
💡 A* 탐색 알고리즘 vs 다익스트라 알고리즘

• 다익스트라 알고리즘
• A* 탐색 알고리즘
• A* 알고리즘은 시작 정점에서 현재 정점 v까지의 경로의 길리 g(v)와 현재 정점 v에서 도착 정점까지의 추정 잔여거리 h(v)를 동시에 고려하는 반면, 다익스트라 알고리즘은 g(v)만을 고려

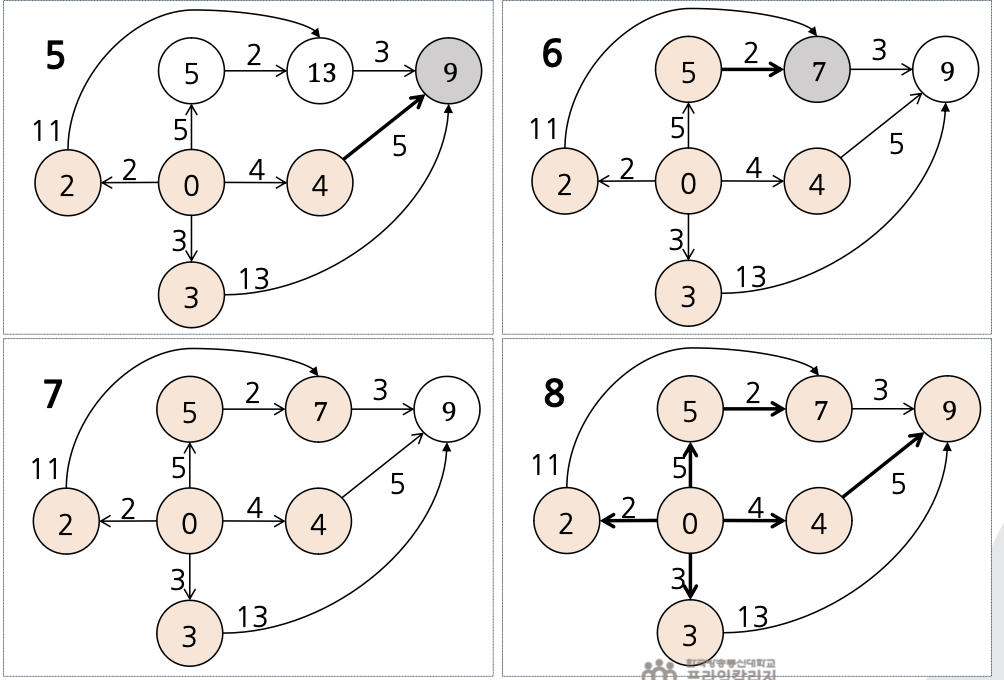
💡 TSP에 A* 탐색 알고리즘을 적용한 예

• 
• 분기한정 탐색과의 차이
  • A* 탐색 알고리즘에서는 리프노드가 방문되는 순간 알고리즘이 끝남
    • 싸이클의 길이가 계산되었지만 방문되지 않은 리프 노드 : 방문된 리프 노드가 나타내는 길이보다 길다는 것을 의미
    • 아직 싸이클의 길이가 계산되지 못한 리프 노드 : 해당 노드들의 조상 노드의 추정 길이기 방문된 리프 노드가 나타내는 길이보다 길다는 것을 의미

💡A* 탐색 알고리즘의 공간복잡도

• 상태공간 트리를 탐색하는 알고리즘이기 때문에 상태공간트리에 비례하는 공간을 차지
  • O(b^d)
    • b : branching factor, 평균 상태 분기 수
      • d : 해에 해당하는 리프 노드의 깊이

📚 4. 몬테카를로 트리 탐색

💡 상태공간 트리 탐색

• 무정보 탐색 : 추가적인 정보나 방향성 없이 탐색(너비우선 탐색(BFS), 깊이우선 탐색(DFS))
• 최적우선 탐색 : 평가 함수에 기반해서 가장 유리한 쪽부터 탐색(다익스트라 알고리즘, A*알고리즘)
• 최소최대 탐색 : 최악의 경우에 입을 손실을 최소화하는 방향으로 탐색

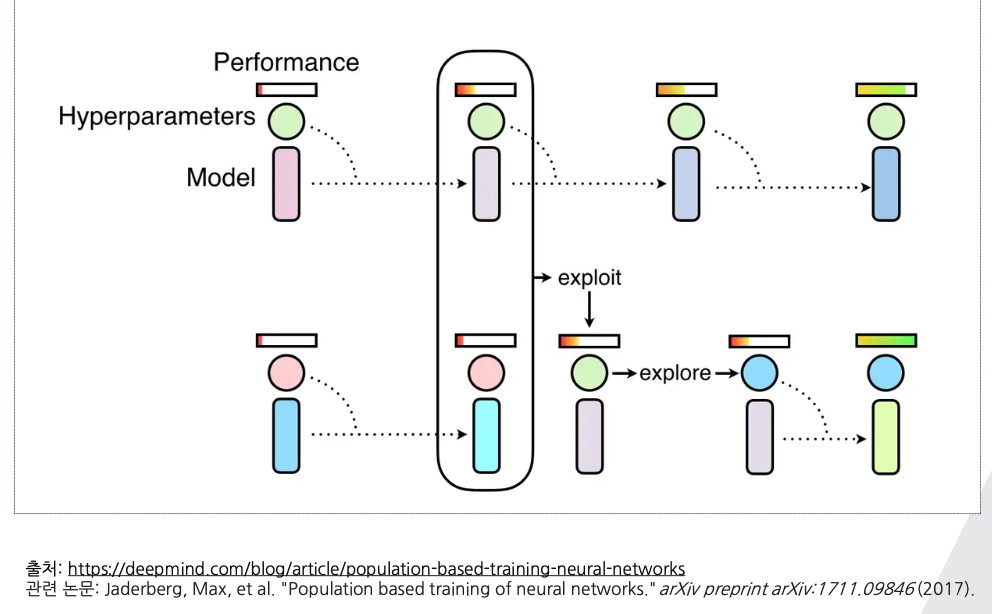
💡 몬테카를로 트리 탐색이란?

• Monte Carlo Tree Search (MCTS)
  • 상태공간 트리 탐색 알고리즘의 일종
  • 랜덤한 시뮬레이션 결과를 이용한 평가함수 개선을 통해 트리를 효율적으로 탐색
  • 알파고, 테슬라의 자율주행 소프트웨어, 게임의 AI등에 사용됨
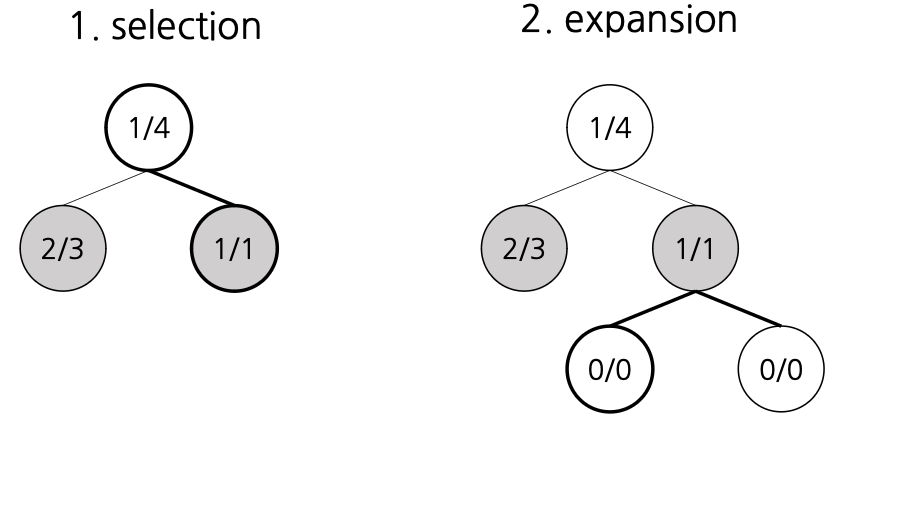
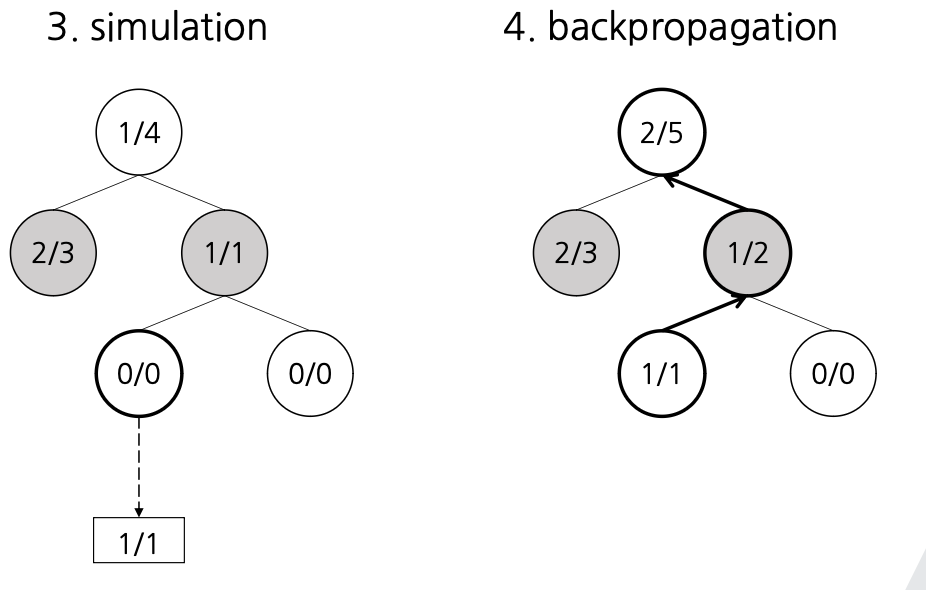
• 몬테카를로 트리 탐색 과정
  • Selection : 루트 노드 R에서부터 시작해서 평가함수를 기준으로 좋은 자식 노드들을 선택해 나감
  • Expansion : 마지막에 선택된 노드가 최종 노드가 아니라면(추가적인 상태의 여지가 있다면) 새로운 자식 노드들을 생성한 뒤 그 중에 하나를 선택(C노드)
  • simulation(evaluation) : C노드로부터 최종겨과가 나올 때까지 전개(roll out)
  • backpropagation(backup) : 최종 결과를 C에서 R에 이르는 경로에 반영
    

💡 몬테카를로 트리 탐색의 아이디어

• expansion 단계에서 선택한 행동(상태)으로부터 파생되는 결과를 모두 확인하는 대신, 랜덤한 시뮬레이션을 통해 그 행동의 결과를 확인하고 평가함수를 지속적으로 개선함으로써 분기가 많은 상태공간을 효율적으로 탐색할 수 있음.
• 여러 번의 시뮬레이션을 통해 어떤 행동의 가치에 대해 추정하는 것이지 모든 겨로가를 확인하는 것이 아니기에 놓치는 결과도 있을 수 있음.