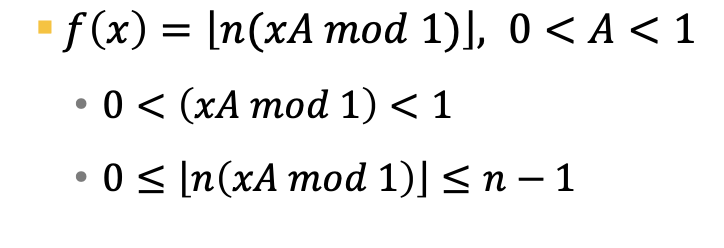해시테이블

채영민·2024년 2월 7일

데이터 구조_파이썬

목록 보기

5/25

📚 1. 해시테이블

💡 해시란?

해시는 원래의 데이터를 일정한 길이의 데이터로 변환하는 과정이나 그 결과를 말함.

💡 해시테이블 이란?

Key를 Value에 연결시키는 자료구조 중 하나로, 해시 함수를 사용해 키를 해시값으로 변환하고 이 해시 값을 인덱스로 사용해 값을 저장하거나 찾는 방법.

원소의 저장 위치가 원소값에 의해 결정되는 데이터 구조를 뜻한다.

💡 해시테이블 특징?

충돌이 없다면, 원소에 대한 접근과 저장을 상수 시간 O(1)에 할 수 있다.

충돌이 있다면 즉 저장하고자 하는 자리에 이미 다른 원소가 들어있다면 추가적인 연산이 필요할 수도 있다.

💡 해시함수 란?

원소를 입력으로 받아 원소가 저장될 위치를 리턴. ex) f(x) = x mod x

해시 함수가 가져야 하는 성질
1. 충돌을 낼 확률이 적어야 한다. (= 해시 테이블 전체를 골고루 사용해야 함.)
2. 계산이 간단해야 함.

📚 2. 충돌 해결 방법들

💡 충돌 해결법

체이닝 : 해시 테이블이 연결리스트로의 링크를 가지게끔 하는 것.

개방주소 : 추가 공간 없이 주어진 해시테이블 내에서 충돌 해결

📚 3. 충돌 해결 방법1 : 체이닝

💡 체이닝 구현 코드

add(x) 

# hash(x) 위치에 저장된 리스트를 x에 추가

	t[hash](x)].append(x) # t = 해시테이블을 나타내는 변수
	return true

find(x)

# 해시테이블에 x가 들어있는지 여부 조사

	for y in t[hash(x)] do # t[hash(x)]가 리스트 이므로 리스트 안의 원소를 차례로 탐색

		if y = x then
        	return true # x가 리스트 안에서 발견될 시.

        return false # x가 리스트 안에서 발견되지 않을 시.

remove(x)

# 해시테이블에서 x를 삭제

	l <- t[hash(x)] # 테이블의 hash(x) 자리가 가리키고 있는 리스트를 가져옴.

	for y in l do

    	if y = x then
        	l.remove_value(y)
			return y # 리스트 안의 x와 같은 원소가 있으면 해당 값을 리스트 내에서 삭제.	
	
	return nil # 해시 테이블에서 x가 발견되지 않으면 nil 리턴.

📚 3. 충돌 해결 방법2 : 개방 주소

💡 충돌 이후 저장위치를 고려하는 방식들

선형 조사

충돌이 일어났을 때, 충돌이 일어난 뒷부분을 연속적으로 살펴보고, 빈 공간을 발견하면 원소 삽입.

해시 테이블의 마지막까지 도달하면 처음으로 돌아가서 계속 탐색. (순환 인덱스)

fi(x) = (g(x) + i) mod n ( i는 몇번째 순환 시도인지를 나타냄, n은 해시테이블의 크기 ).

한 곳에 원소가 몰리게 되면 성능이 급격하게 떨어짐.

이를 1차 군집 (primary clustering)이라고 함.

군집이 있는 곳은 군집이 없는 곳에 비해 영역이 더 빨리 커짐.

군집 여러 개가 하나로 합쳐지기도 함.

ex) [- , - , - , - , 12 , - , 4 , 24 , 54 , - , -] (x mod 10 테이블)
* 위 해시테이블에서 4,24,54가 모여있는 덩어리가 군집.

이차원 조사

충돌이 일어난 바로 뒷부분을 살펴보는 대신, 검사하는 인덱스 간격을 이차함수를 이용해 증가시킨다.

fi(x) = (g(x) + k1i^2 + k2i) mod n ( i는 몇번째 순환 시도인지를 나타냄, n은 해시테이블의 크기 ).

ex) g(x) = x mod 10, k1 = 1, k2 = 0, x = 64

[- , - , - , - , 12 , - , 4 , 24 , 54 , 34 , -]

선형 조사 방법으로는 5번째 시도에 64의 삽입이 일어나지만, 이차원 조사로는 3번째 시도에 삽입이 됨.

같은 해시값을 갖는 원소의 경우에, 이차원 조사 방법을 사용해도 결과적으로는 같은 인덱스를 검사하기에 여전히 군집현상이 생긴다.

ex) g(x) = x mod 10, k1 = 1, k2 = 0, x = 74

이차원 조사로는 4번째 시도에 삽입이 되지만 선형 조사로도 4번째 시도에 64의 삽입이 일어남, 충돌시에 검사하는 해시값이 같기 때문에 형태만 다를 뿐이니 이차원 조사에도 군집을 이루게 된다고 볼 수 있음.

더블 해싱

해시 함수 2개를 사용해서 해시값을 계산하는 방법.

fi(x) = (g(x) + ih(x)) mod n

두 원소의 g(x)값이 같아도 h(x)까지 같을 확률은 매우 낮기에 2차 군집이 발생하지 않는다.

💡 개방 주소 기반에 해시 테이블 구현 코드

find(x)
# 해시테이블에 x가 들어있는지 여부 조사

	# x의 첫번째 해시값 계산
	i <- 0
    j <- hash(x, i)
   
    # 탐색한 자리가 nil이거나, 테이블 전체 크기만큼 검사를 해도 x를 찾지 못하면,
	# 루프를 끝내고 false 리턴
    while t[j] != nil and i < size(t) do
    	if t[j] = x then 
			return true # 탐색한 자리에 x가 존재 시

		# 탐색한 자리에 x가 없으면 다음에 탐색할 인덱스를 생성
		i <- i + 1            
		j <- hash(x, i) 

	return false       

remove(x)
# 해시테이블에서 x를 삭제

	# x의 첫번째 해시값을 계산
	i ← 0
	j ← hash(x, i)
   
	# 탐색한 자리가 nil이거나
	# 테이블 전체 크기만큼 탐색을 반복했을 때도 x를 찾지 못하면 루프를 끝내고 false를 리턴
	while t[j] != nil and i < size(t) do
   
		if t[j] = x then
			t[j] ← del
			return true # x가 발견되면 그 자리에 del을 저장
           
		# 탐색한 자리에 x가 없으면 다음에 탐색할 인덱스를 생성
		i ← i + 1
		j ← hash (x, i)
       
	return false
  
add(x)
# 해시테이블에 x를 추가

	i ← 0
	# x의 첫번째 인덱스를 계산
	j ← hash(x, i)
	# 탐색 횟수가 테이블 전체 크기를 넘지 않는 동안만 시도
   
	while i < size(t) do
		# nil이나 del 또는 이미 저장된 x를 발견하면 x를 저장
       
		if t[j] = nil or t[j] = del or t[j] = x then
			t[j] ← x
			return true
           
		# t[j]에 x를 삽입할 수 없으면 다음에 탐색할 인덱스를 생성
		i ← i + 1
		j ← hash(x, i)
       
	return false