정렬배열과 트리, 이진트리

📚 1. 정렬배열

💡 정렬배열이 나오게 된 배경

• 원소들의 순서를 유지해야 하는 경우가 있을 수 있음.
• 선형 계열 데이터 구조를 사용하고 원소가 삽입될 때마다 정렬하는 방법.
  • 정렬의 O(nlogn) 시간이 소요.
  • 정렬된 형태를 유지하는 구조가 필요.

💡 정렬배열이란

• 원소가 항상 정렬된 형태를 유지하는 배열.
• 삽입 삭제시 O(n) 시간이 소요.
• 정렬배열에서의 검색.
  • 선형 검색 : O(n) 이 소요.
  • 이진 검색 : 배열의 중앙에서 부터 시작해 절반씩 범위를 좁혀가며 검색, O(logn)이 소요
• 정렬배열의 삽입 / 삭제에 걸리는 O(n) 시간은 데이터의 삽입 / 삭제가 빈번하게 일어나는 환경에서는 너무 김.

📚 2. 트리

💡 트리란

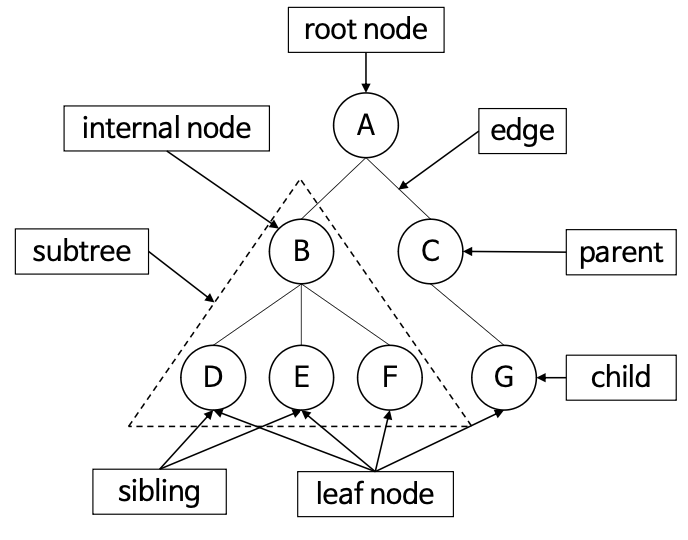
💡 트리의 구성 요소

• edge(간선) : 노드를 연결하는 선
• parent node
• child node
• sibling(형제 노드) : 같은 부모를 가지는 노드
• root node : 최상위 노드, 부모가 없는 노드
• leaf node(단말 노드) : 자식이 없는 노드
• internal node : 리프 노드가아닌 노드

💡 트리에서 사용되는 용어

• 노드의 차수(degree)
  • 노드의 자식 수, 리프 노드는 0
  • B의 차수 : 3 (위 그림에서)
  • C의 차수 : 1
• 트리의 차수(degree of tree)
  • 트리가 가진 노드의 차수 중 최대 값
  • A를 루트로 가지는 트리의 차수 : 3 (위 그림에서)

📚 3. 이진트리

💡 이진트리란

• 각 노드가 최대 두 개의 자식 노드를 갖는 트리

💡 노드의 깊이란

• 노드에서 루트 노드까지의 경로의 길이(=level)
  

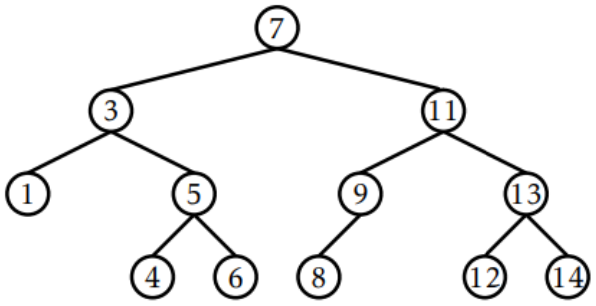
• ex) 6의 깊이 : 3, 9의 깊이 : 2, 7의 깊이 : 0 (위 그림에서)

depth(u)
	d <- 0
	while (u != r) do
		u <- u.parent
        d <- d + 1
	return d       

💡 노드의 크기란

• 노드 자신을 포함한 모든 자식 노드의 개수
• ex) 5의 크기 : 3, 11의 크기 : 6 (위 그림에서)

size(u)
	if u = nil then return 0
    return 1 + size(u.left) + size(u.right)

💡 노드의 높이란

• 노드에서 노드 아래에 있는 리프 노드까지의 경로 중 가장 긴 경로의 길이
• ex) 3의 높이 : 2, 7의 높이 : 3, 6의 깊이 : 0 (위 그림에서)

get_height(u)
	return height(u) - 1

height(u)
	if u = nil then return 0
    return 1 + max(height(u.left), height(u.right))

💡 트리의 순회란

• 트리의 노드들을 차례대로 방문하는 것

traverse(u)
	if u = nil then return
    traverse(u.left)
    traverse(u.right)

💡 너비 우선(breadth-first) 순회란

• 트리의 각 레벨별로 탐색을 하는 것

bf_traverse()
	q <- arrayQueue()
    if r != nil. then q.add(r)
    while q.size() > 0 do
    	u <- q.remove()
        if u.left != nil then q.add(u.left)
        if u.right !- nil then q.add(u.right)