Heap이란?
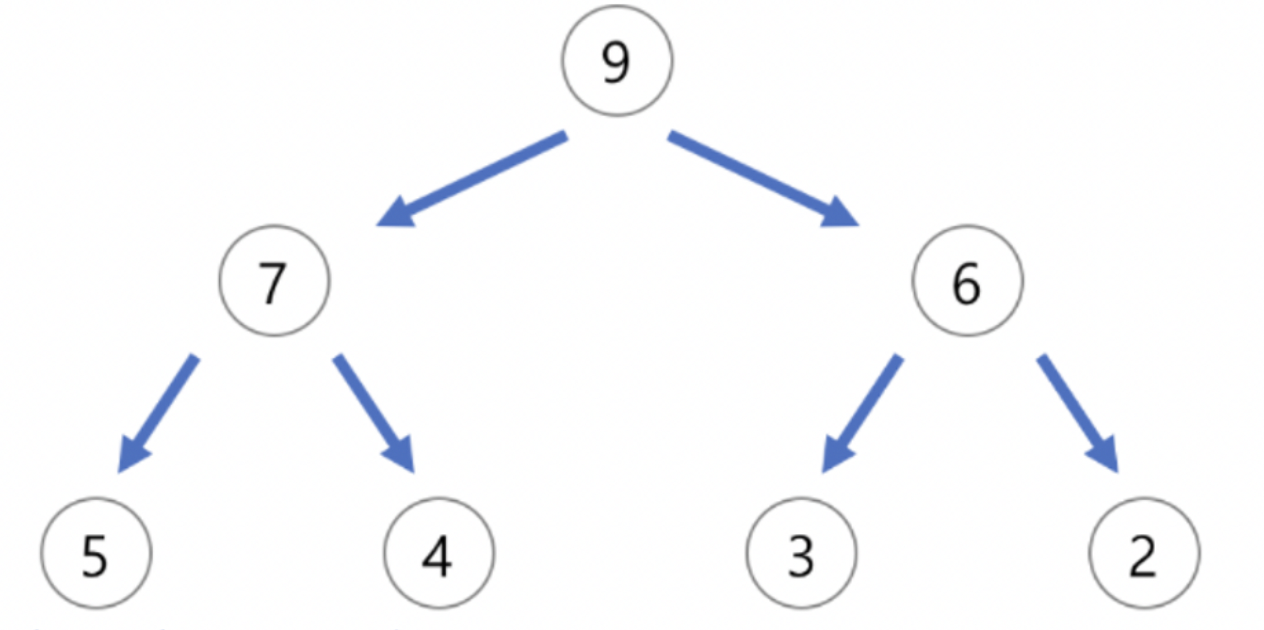
Heap의 특징
- 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
- 힙은 일종의 반정렬 상태(느슨한 정렬 상태) 를 유지한다.
- 최대힙 기준
- 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 이진 트리를 말한다.
- 최소힙 기준
- 작은 값이 상위 레벨에 있고 큰 값이 하위 레벨에 있다
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작은 이진 트리를 말한다.
- 최대힙 기준
- 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)
-
heap의 종류
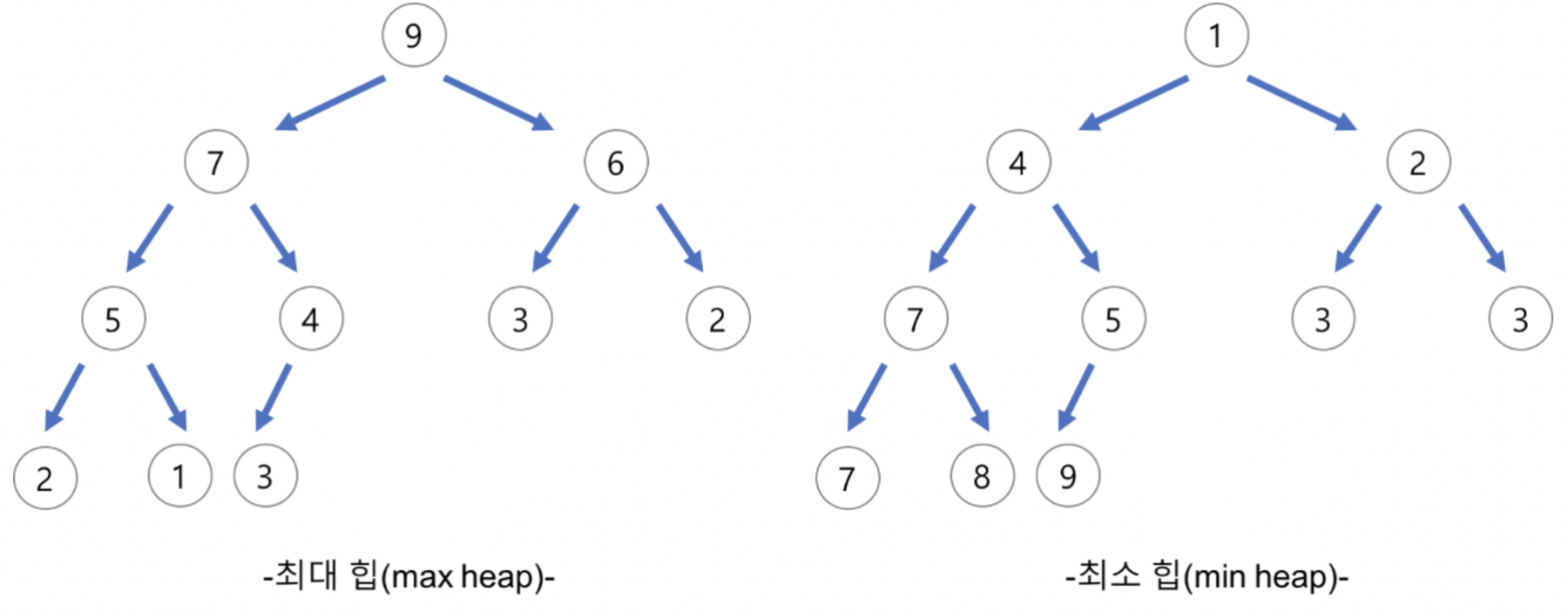
- 최대 힙(max heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- key(부모 노드) >= key(자식 노드)
- 최소 힙(min heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
- key(부모 노드) <= key(자식 노드)
- 최대 힙(max heap)
Tree의 용어
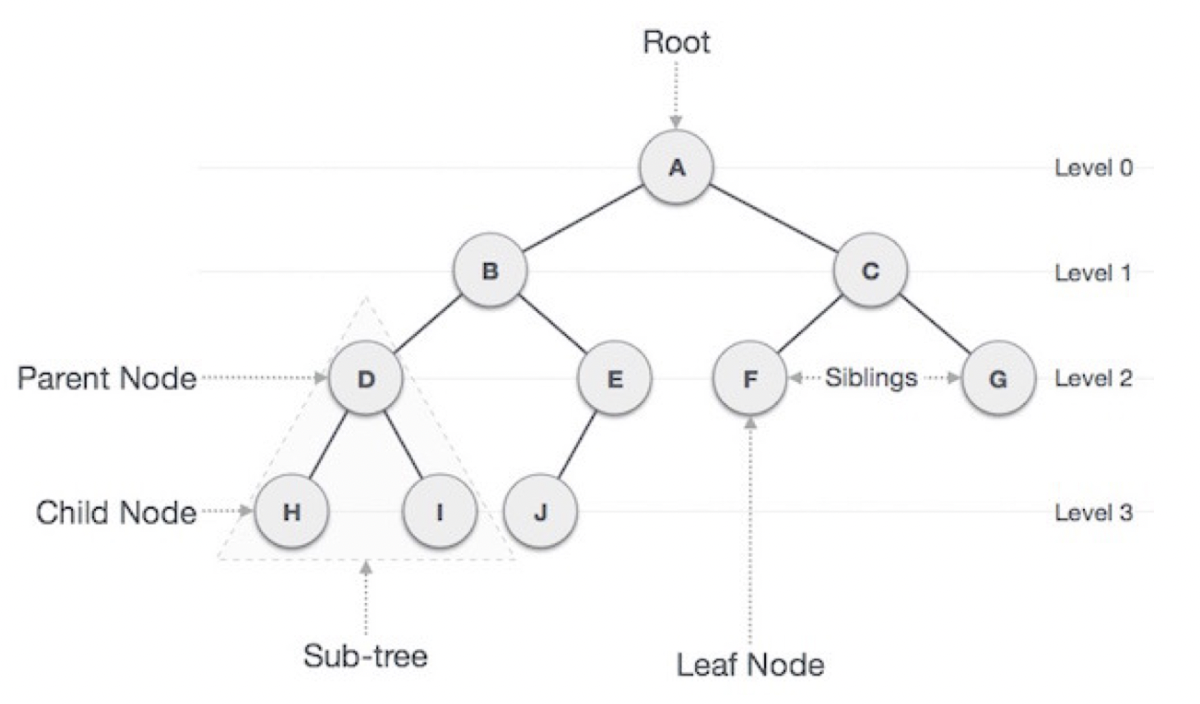
- 루트 노드(root node) : 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
- 단말 노드(leaf node) : 자식이 없는 노드, ‘말단 노드’ 또는 ‘잎 노드’라고도 부른다.
- 내부(internal) 노드 : 단말 노드가 아닌 노드
- 간선(edge) : 노드를 연결하는 선 (link, branch 라고도 부름)
- 형제(sibling) : 같은 부모를 가지는 노드
- 노드의 크기(size) : 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- 노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합
- 노드의 차수(degree) : 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
- 트리의 차수(degree of tree) : 트리의 최대 차수
- 트리의 높이(height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이
Heap의 구현
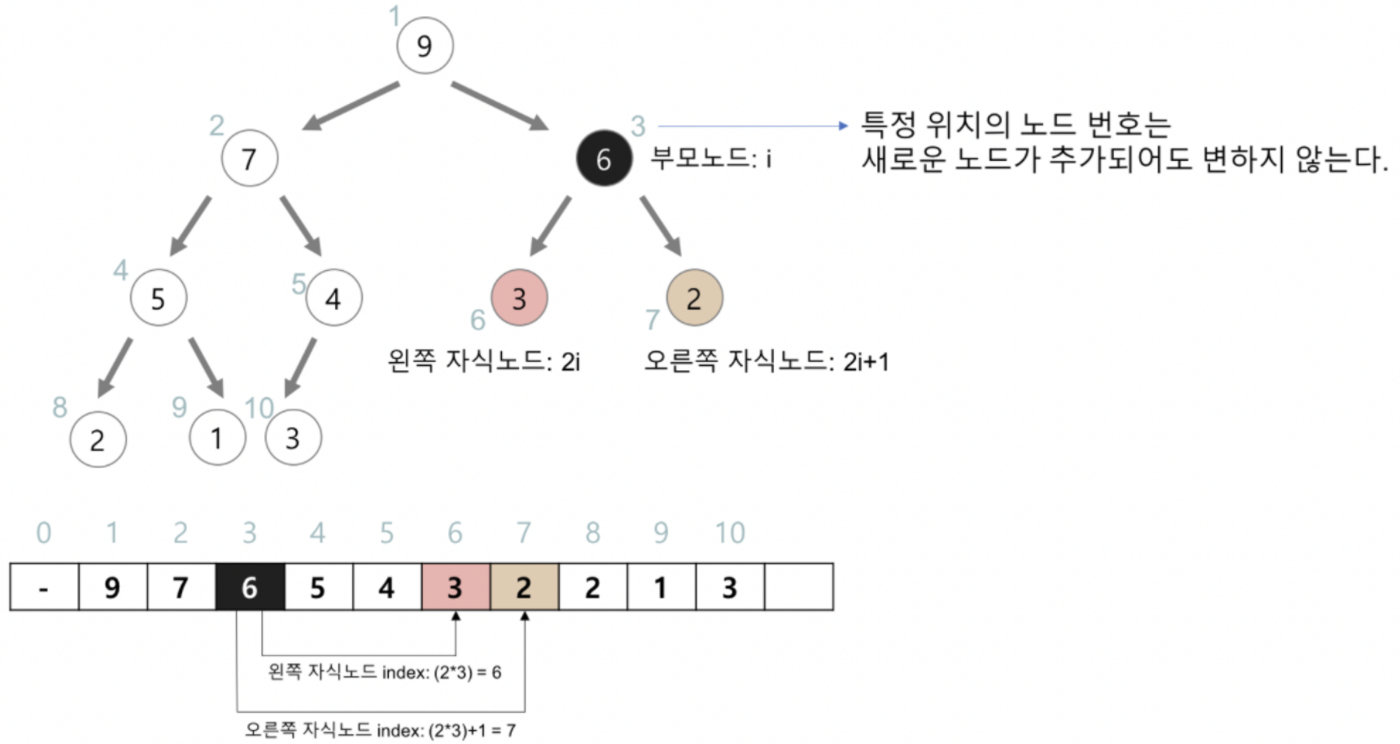
- 힙을 저장하는 표준적인 자료구조는 배열
- 구현을 쉽게 하기 위하여 배열의 첫 번째 인덱스인 0은 사용되지 않는다.
- 특정 위치의 노드 번호(인덱스)는 새로운 노드가 추가되어도 변하지 않는다.
- 힙에서의 부모 노드와 자식 노드의 관계 ( 힙의 성질 )
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스) / 2
-
Heap의 삽입
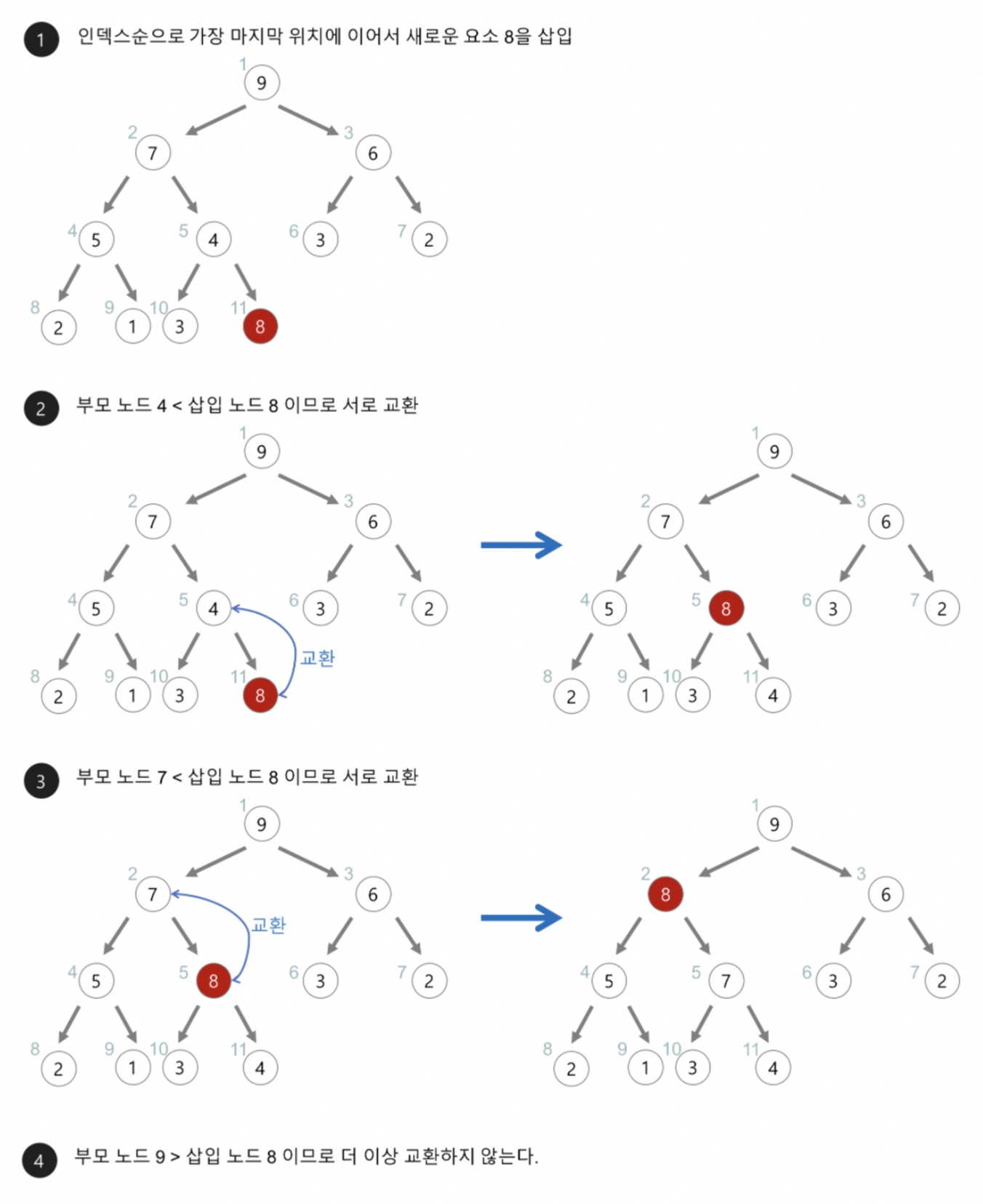
- 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
- 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.
-
Heap의 삭제
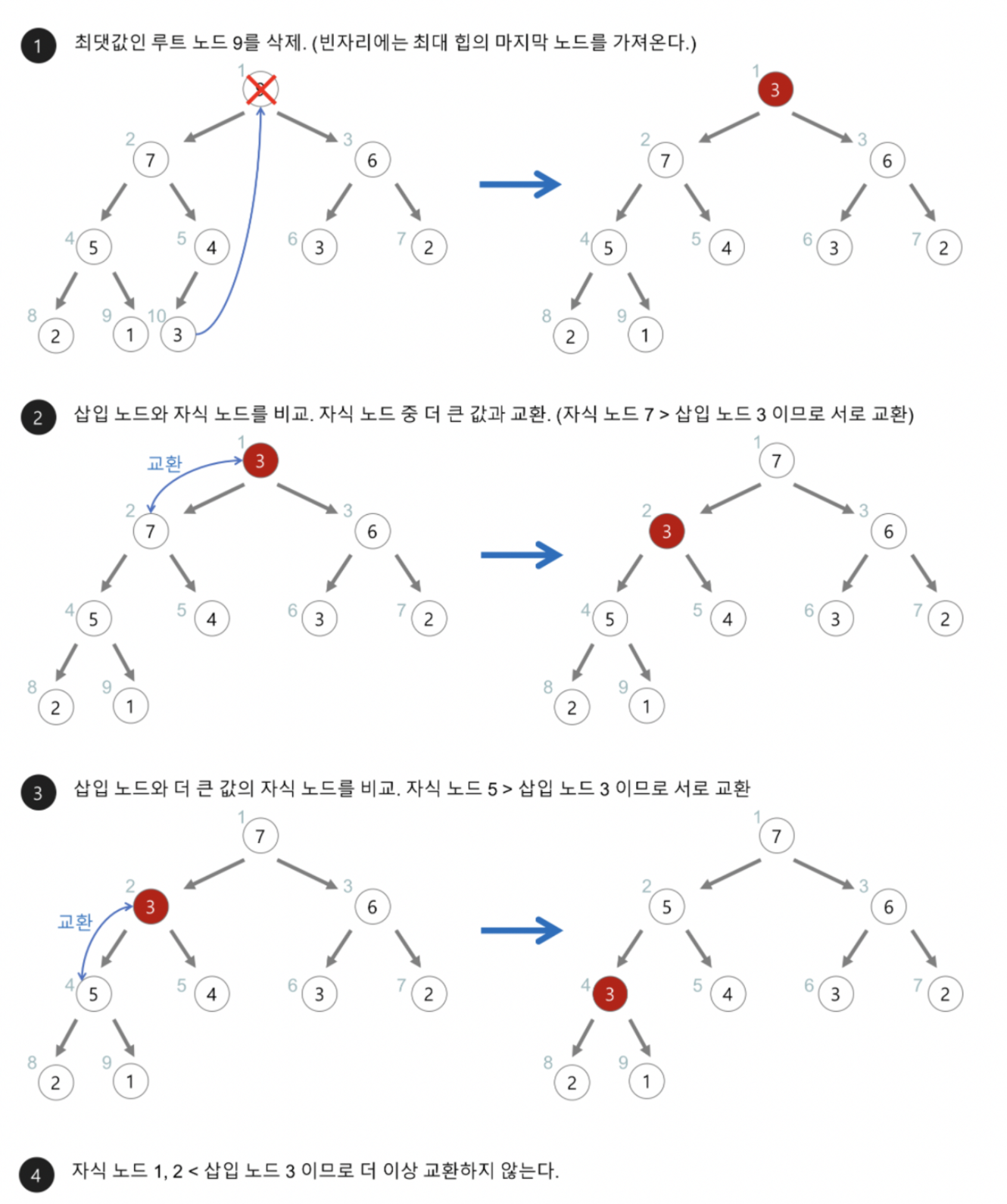
- 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.
⇒ 최대 힙(max heap)에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것 - 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
- 루트 노드에서부터 자식 노드 방향으로 교환하여 힙의 성질을 만족시킨다.
- 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.
JAVA HEAP 구현
MaxHeap 구현 코드import java.util.Arrays;
class MaxHeap {
private int[] heap;
private int maxSize = 10;
public MaxHeap() {
heap = new int[maxSize];
heap[0] = 0;
}
private int getParent(int index) {
return index / 2;
}
private int getLeftChild(int index) {
return index * 2;
}
private int getRightChild(int index) {
return index * 2 + 1;
}
private void swap(int index1, int index2) {
int temp = heap[index1];
heap[index1] = heap[index2];
heap[index2] = temp;
}
private int bigger(int index1, int index2) {
return heap[index1] > heap[index2] ? index1 : index2;
}
private void upHeapify() {
int rearIndex = heap[0];
while (rearIndex > 1 && heap[getParent(rearIndex)] < heap[rearIndex]) {
swap(rearIndex, getParent(rearIndex));
rearIndex /= 2;
}
}
private void downHeapify() {
int rootIndex = 1;
//왼쪽 자식의 존재는 조건에서 이미 존재하는 것으로 확인
while (rootIndex * 2 <= heap[0]) {
// 우측 자식이 존재 했을 경우
if (rootIndex * 2 + 1 <= heap[0]) {
// 좌측 우측 비교후 swap
int bigger = bigger(getLeftChild(rootIndex), getRightChild(rootIndex));
if (heap[rootIndex] >= heap[bigger]) {
break;
}
swap(rootIndex, bigger);
rootIndex = bigger;
} else { // 좌측 자식만 존재하는 경우
if (heap[rootIndex] >= heap[getLeftChild(rootIndex)]) {
break;
}
swap(rootIndex, getLeftChild(rootIndex));
rootIndex *= 2;
}
}
}
private void resize() {
maxSize *= 2;
int[] newHeap = Arrays.copyOf(heap, maxSize);
heap = newHeap;
}
public void add(int value) {
if (heap[0] + 1 >= maxSize) {
resize();
}
heap[++heap[0]] = value;
upHeapify();
}
public int extractRoot() {
int root = heap[1];
heap[1] = heap[heap[0]];
heap[heap[0]] = 0;
heap[0]--;
downHeapify();
return root;
}
public void printHeap() {
for (int i = 0; i < heap.length; i++) {
System.out.println("index = " + i + ", value = " + heap[i]);
}
}
}MinHeap 구현 코드
import java.util.Arrays;
class MinHeap{
private int[] heap;
private int maxSize = 10;
public MinHeap(){
heap = new int[maxSize];
heap[0] = 0;
}
private int getParent(int index) {
return index/2;
}
private int getLeftChild(int index) {
return index * 2;
}
private int getRightChild(int index) {
return index * 2 + 1;
}
private void swap(int index1, int index2) {
int temp = heap[index1];
heap[index1] = heap[index2];
heap[index2] = temp;
}
private int smaller (int index1 ,int index2){
return heap[index1] < heap[index2] ? index1 : index2;
}
private void upHeapify() {
int rearIndex = heap[0];
while(rearIndex>1&&heap[getParent(rearIndex)]>=heap[rearIndex]){
swap(rearIndex,getParent(rearIndex));
rearIndex /= 2;
}
}
private void downHeapify() {
int rootIndex = 1;
//왼쪽 자식의 존재는 조건에서 이미 존재하는 것으로 확인 됨
while (rootIndex * 2 <= heap[0]) {
// 우측 자식이 존재 했을 경우
if (rootIndex * 2 + 1 <= heap[0]) {
// 좌측 우측 비교후 swap
int smaller = smaller(getLeftChild(rootIndex), getRightChild(rootIndex));
if(heap[rootIndex]<= heap[smaller]){
break;
}
swap(rootIndex,smaller);
rootIndex = smaller;
}else{ // 좌측 자식만 존재하는 경우
if (heap[rootIndex] <= heap[getLeftChild(rootIndex)]) {
break;
}
swap(rootIndex, getLeftChild(rootIndex));
rootIndex *= 2;
}
}
}
private void resize() {
maxSize *= 2;
int[] newHeap = Arrays.copyOf(heap, maxSize);
heap = newHeap;
}
public void add(int value) {
if(heap[0]+1 >= maxSize){
resize();
}
heap[++heap[0]] = value;
upHeapify();
}
public int extractRoot() {
int root = heap[1];
heap[1] = heap[heap[0]];
heap[heap[0]] = 0;
heap[0]--;
downHeapify();
return root;
}
public void printHeap() {
for (int i = 0; i < heap.length; i++) {
System.out.println("index = "+i+", value = "+heap[i]);
}
}
}
Heap은 왜 사용하는가
힙의 형태를 보면 최대 힙의 경우 루트가 항상 최댓값이고, 최소 힙의 경우 루트가 항상 최솟값이되기에 이 형질을 이용하여
-
우선순위 큐(priority queue) 구현시의 내부 자료구조
-
힙 정렬(heap sort)
에 사용 된다.
Heap의 시간복잡도
add() : O(log n)
extractRoot() : O(log n)