트리(Tree)란?

트리(Tree)란?

• 정의 : 트리는 노드들이 나무 가지 처럼 연결된 비선형 계층적 자료구조이다.

---

Tree의 특징

• 하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 된다.
• 데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조 이다.
• 트리내에 또 다른 트리가 있는 재귀적 자료구조 이다.
• 단순 순환(Loop)을 갖지 않고 , 연결된 무방향 그래프 구조 이다.
• 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조 이며 모든 자식 노드는 하나의 부모 노드만 갖는다 .
• 노드가 n개인 트리는 항상 n-1개의 간선(edge)을 갖는다 .

---

트리의 구조

• Node : 트리를 구성하고 있는 기본 요소, 노드에는 키 또는 값과 하위 노드에 대한 포인터를 가진다.
  
  
• Edge : 노드와 노드 간의 연결선
  
  
• Root Node : 트리 구조에서 부모가 없는 최상위 노드
  
  
• Parent Node : 자식 노드를 가진 노드
  
  
• Child Node : 부모 노드의 하위 노드
  
  
• Sibling Node : 같은 부모를 가지는 노드
  
  
• Branch Node : 자식 노드가 하나 이상 가진 노드
  
  
• Leaf Node : 자식 노드가 없는 노드
  
  
• depth : 루트에서 어떤 노드까지의 간선의 수, 루트 노드의 깊이는 0
  
  
• height : 어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수
  
  
• Level : 루트에서 어떤 노드까지의 간선(Edge) 수
  
  
• Degree : 노드의 자식 수
  
  
• Path : 한 노드에서 다른 한 노드에 이르는 길 사이에 놓여있는 노드들의 순서
  
  
• Path Length : 해당 경로에 있는 총 노드의 수
  
  
• Size : 자신을 포함한 자손의 노드 수
  
  
• Width : 레벨에 있는 노드 수
  
  
• Breadth : 리프 노드의 수
  
  
• Distance : 두 노드 사이의 최단 경로에 있는 간선(Edge)의 수
  
  
• Order : 부모 노드가 가질 수 있는 최대 자식의 수

---

Tree의 순회

• 트리 구조에서 각각의 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정을 트리의 순회라고 하며 이는 노드를 방문하는 순서에 따라 분류된다

  • 전위 순회(Pre-Order)

    

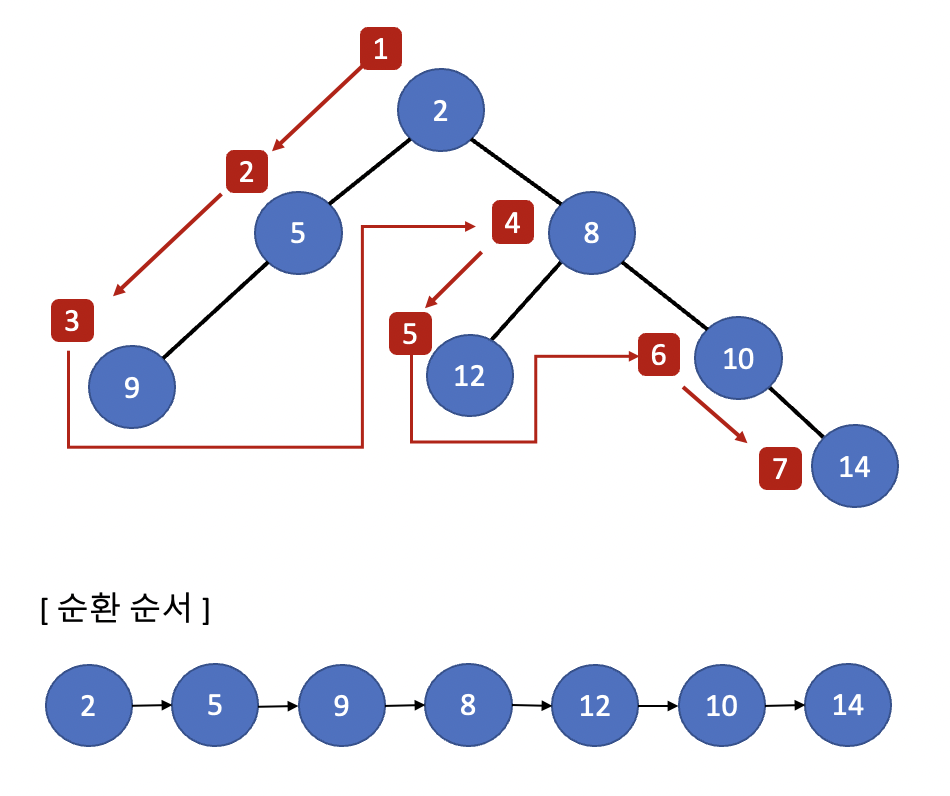
    1. 시작 노드를 방문한다.

    2. 왼쪽 서브 트리를 순회한다.

    3. 오른쪽 서브 트리를 순회한다.

       ⇒ 전위 순회는 깊이 우선 순회(depth-first traversal)라고도 한다.
       
       

  • 중위 순회(In-order)

    

    1. 왼쪽 서브 트리를 순회한다.

    2. 시작 노드를 방문한다.

    3. 오른쪽 서브 트리를 순회한다.

       ⇒ 중위 순회는 대칭 순회(symmetric)라고도 한다.

• 후위 순회(Post-order)

  

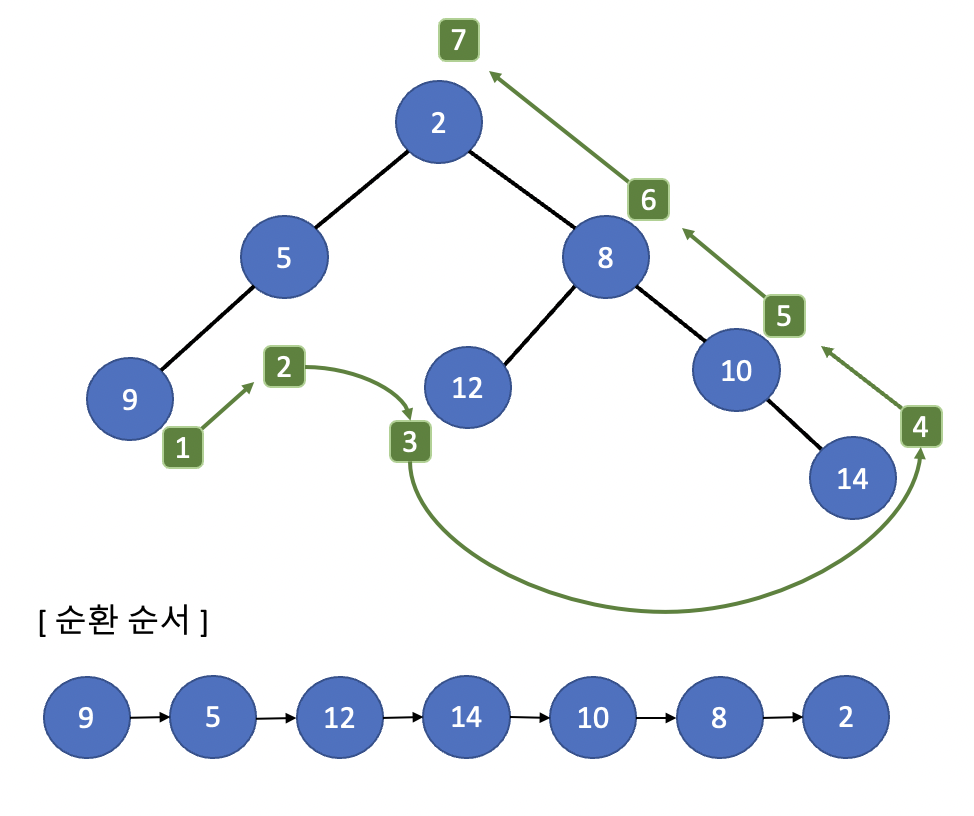
  1. 왼쪽 서브 트리를 순회한다.
  2. 서브 트리를 순회한다.
  3. 시작 노드를 방문한다.

---

Tree의 용도

계층 적 데이터 저장

• 트리는 데이터를 계층 구조로 저장하는 데 사용한다.
• 예를 들어 파일 및 폴더는 계층적 트리 형태로 저장된다.

효율적인 검색 속도

• 효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용한다.

힙(Heap)

• 우선순위큐를 구현하기 위해 사용되는 자료구조인 힙(Heap) 구조 또한 트리의 일종이다.

데이터 베이스 인덱싱

• 데이터베이스 인덱싱을 구현하는데 트리를 사용한다.
• 예) B-Tree, B+Tree, AVL-Tree..

Trie

• 사전을 저장하는 데 사용되는 특별한 종류의 트리이다.

---

참고

트리 참고