정렬(Sort)이란?
- 정렬 이란?
정의 : 데이터의 집합을 어떠한 기준을 가지고 번호순이나 사전 순서와 같이 일정한 순서로 열거하는 것 이다.
- 정렬 알고리즘이란?
정의 : n개의 숫자가 주어졌을 때 이를 사용자가 지정한 기준에 맞게 정렬하는 알고리즘 이다.
Stable Sort vs not Stable Sort
-
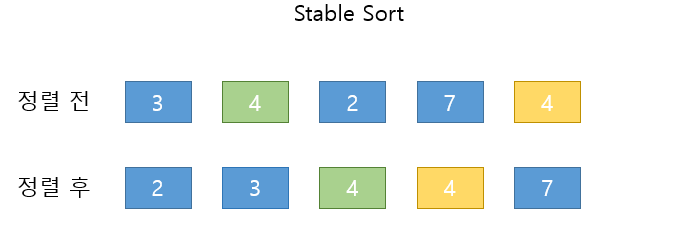
Stable Sort
정의 : 어떠한 정렬 알고리즘으로 정렬 했을 때 항상 중복 된 키 값이 처음 위치 순서대로 정렬 되었다면 stable sort 라고 한다.위의 사진의 중복 요소를 기준으로 정렬 전 4와 4의 순서와 정렬 후 4와 4의 순서가 동일할 경우 Stable sort 라고 한다.
-
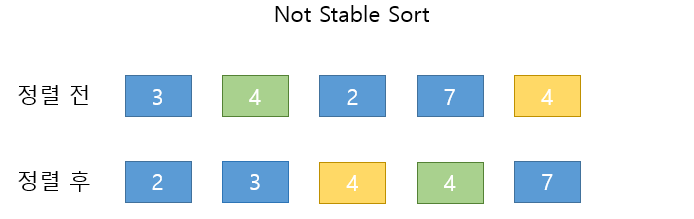
not Stable Sort
정의 : 어떠한 정렬 알고리즘으로 정렬 했을 때 중복 된 키 값이 처음 위치 순서대로 정렬이 되어 있지 않다면 Not Stable sort 라고 한다.위의 사진의 중복 요소를 기준으로 정렬 전 4와 4의 순서와 정렬 후 4와 4의 순서가 동일 하지 않을 경우 not Stable sort 라고 한다.
in-place sort vs not in-place sort
- in-place
정의 : in-place 정렬은 어떠한 정렬 알고리즘으로 정렬 했을 때 원소들의 개수에 비해 충분히 무시할 만한 저장 공간만을 더 사용하는 정렬 알고리즘 이라고 할 수 있다.
위의 사진과 같이 두 요소를 교환하여 정렬을 할 경우 교환을 위한 temp 변수 이외의 저장공간이 더 필요 없는 것과 같이 충분히 무시할 만한 저장 공간만을 더 사용하는 정렬을 in-place 정렬이라고 한다.
- not in-place
정의 : not in-place 정렬은 어떠한 정렬 알고리즘으로 정렬 했을 때 원소들의 개수에 비례하여 저장 공간을 더 사용하는 정렬 알고리즘 이라고 할 수 있.
위의 사진과 같이 새로운 배열을 생성하여 요소를 삽입하는 정렬을 할 경우 요소 n개 만큼의 새로운 저장 공간을 필요로 하는 것과 같이 소들의 개수에 비례하여 저장 공간을 더 사용하는 정렬을 not in-place 정렬 이라고 한다.
선택 정렬 (Selection Sort)
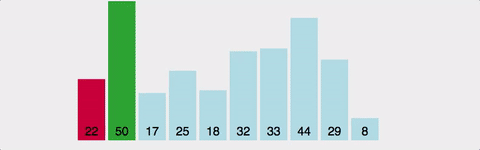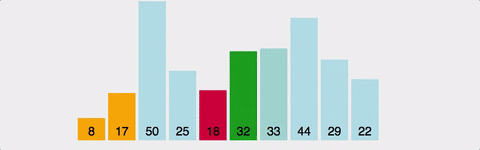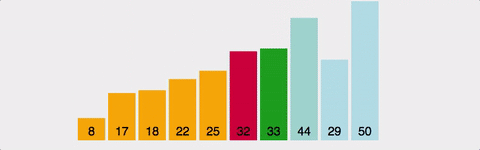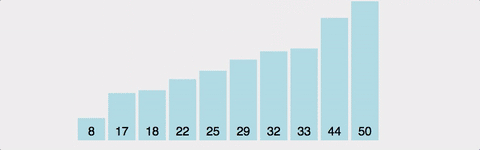
-
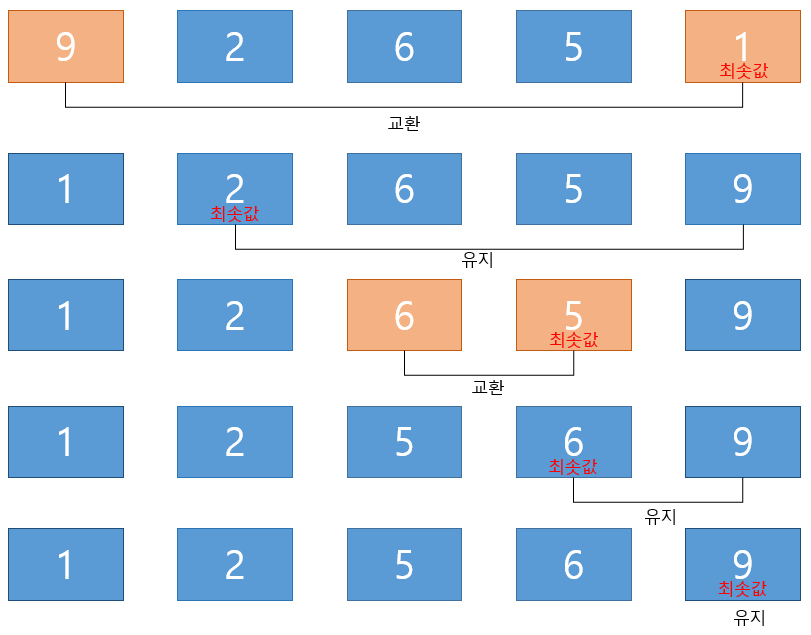
정의 : 선택정렬은 현재 위치에 들어갈 값을 찾아서 swap 하는 알고리즘 이다.
-
선택 정렬 방법 (오름차순)
1. 정렬이 되지 않은 배열의 0번 인덱스 선택
2. 선택한 인덱스 이후 요소들중 최솟값을 찾음
3. 선택한 인덱스의 요소와 최솟값 요소를 swap
4. 인덱스 값 ++
[2~4번 반복한다.]
- 특징
- 하나의 배열에서 값을 swap 하는 식으로 동작하기 때문에 공간 복잡도 O(1)이다.
- swap시 임시 변수 하나 공간 정도가 더 필요하기 때문에 in-place 정렬이다.
- 탐색은 (n - 1),(n - 2),(n - 3) … 1 번 진행 되므로 시간 복잡도 O(n^2) 이다.
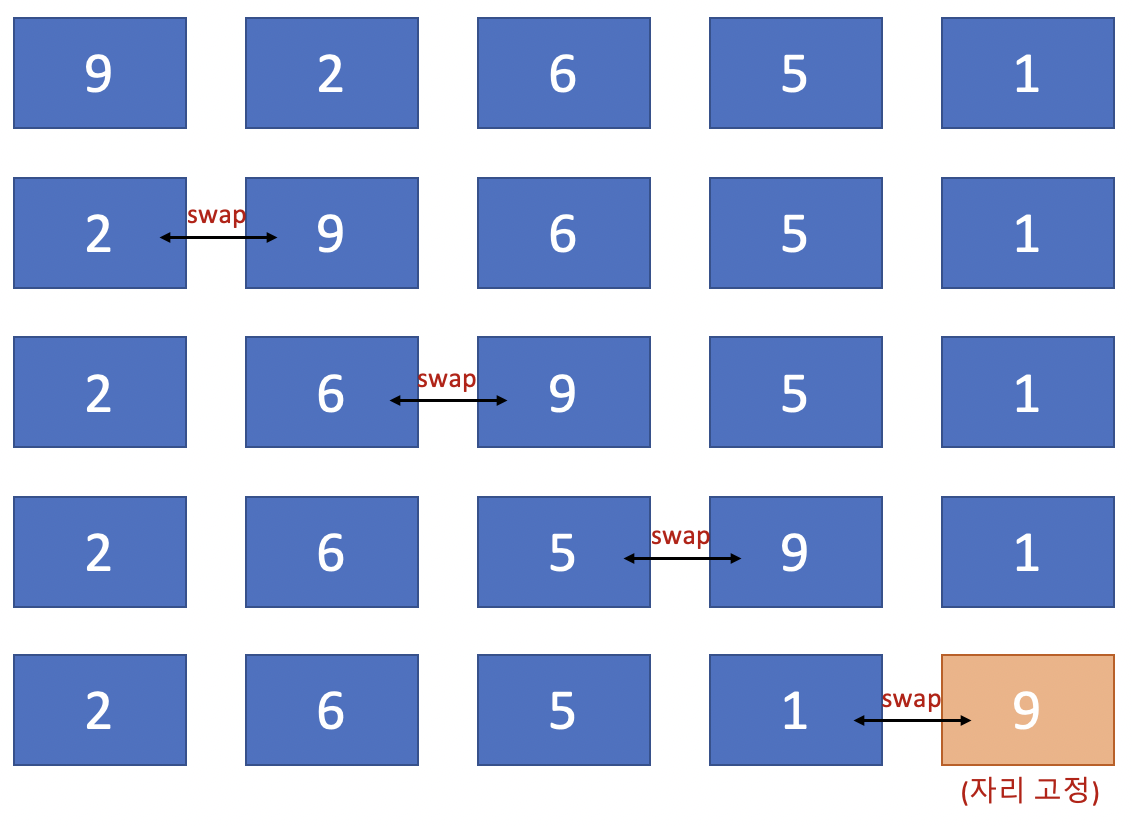
- 중복 키 값이 순서대로 바뀌지 않을 수 있기 때문에 not stable sort 이다.
- 예시) {7, 7, 1} 선택 정렬
-
구현 코드
class Sort { public void selectionSortAsc(int[] arr) { //오름차순 int min; for (int i = 0; i < arr.length; i++) { min = i; for (int j = i + 1; j < arr.length; j++) { if (arr[j] < arr[min]) { min = j; } } if (min != i) { swap(arr, min, i); } } } public void selectionSortDesc(int[] arr) { //내림차순 int max; for (int i = 0; i < arr.length; i++) { max = i; for (int j = i + 1; j < arr.length; j++) { if (arr[j] > arr[max]) { max = j; } } if (max != i) { swap(arr, max, i); } } } public void swap(int[] arr, int index1, int index2) { int temp = arr[index1]; arr[index1] = arr[index2]; arr[index2] = temp; } }
버블 정렬(Bubble Sort)
 * 정의 : 버블 정렬은 현재 원소와 다음 원소를 비교하여 swap 하는 식의 정렬 알고리즘 이다.
⇒ 원소가 거품처럼 올라오는 듯 하여 버블 정렬이라는 이름이 붙음
* 정의 : 버블 정렬은 현재 원소와 다음 원소를 비교하여 swap 하는 식의 정렬 알고리즘 이다.
⇒ 원소가 거품처럼 올라오는 듯 하여 버블 정렬이라는 이름이 붙음
- 버블 정렬 방법 (오름차순)
 (...반복)
(...반복)
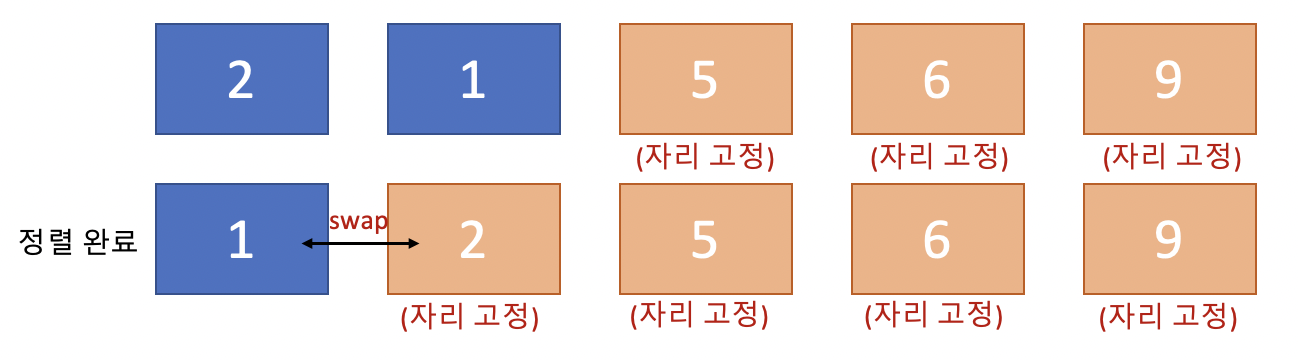
- 정렬이 되지 않은 배열의 0번 인덱스부터 선택
- 선택한 인덱스의 요소와 인접한 다음 요소와 크기 비교
- 선택한 인덱스 요소보다 인접한 요소가 작다면 swap
- 선택한 인덱스 요소보다 인접한 요소가 크다면 no swap
- 선택한 인덱스 ++
[2~3번 반복한다.]
- 특징
- 하나의 배열에서 값을 swap 하는 식으로 동작하기 때문에 공간 복잡도 O(1)이다.
- 선택 정렬과 마찬가지로 swap 시에 필요한 임시 변수 정도의 추가 공간만 있으면 되므로 in-place 정렬이다.
- 탐색은 (n - 1),(n - 2),(n - 3) … 1 번 진행 되므로 시간 복잡도는 O(n^2) 이다.
- 버블 정렬은 중복된 키 값의 순서가 정렬 이후에도 유지되므로 stable 정렬이다.
-
구현 코드
class Sort { public void bubbleSortAsc(int[] arr) { // 오름차순 for (int i = 0; i < arr.length; i++) { for (int j = 1; j < arr.length-i; j++) { if(arr[j-1]>arr[j]) swap(arr,j,j-1); } } } public void bubbleSortDesc(int[] arr) { //내림차순 for (int i = 0; i < arr.length; i++) { for (int j = 1; j < arr.length-i; j++) { if(arr[j-1]<arr[j]) swap(arr,j,j-1); } } } public void swap(int[] arr, int index1, int index2) { int temp = arr[index1]; arr[index1] = arr[index2]; arr[index2] = temp; } }
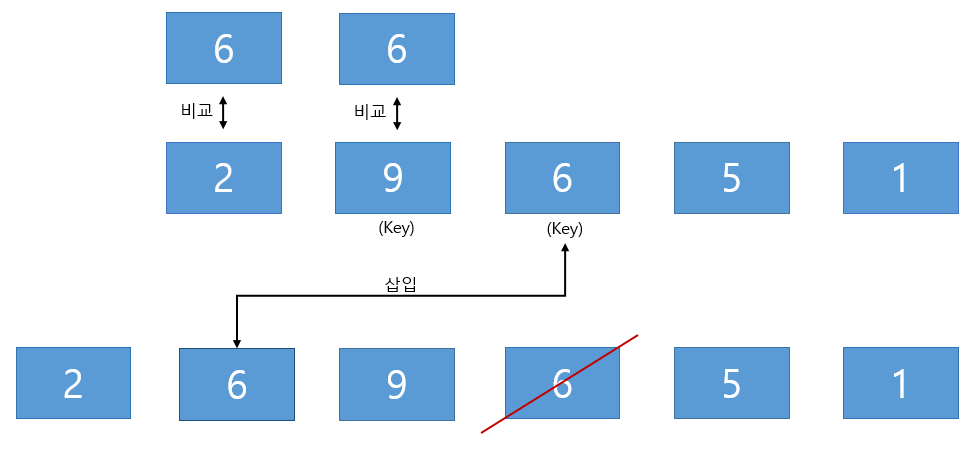
삽입 정렬(Insertion Sort)
-
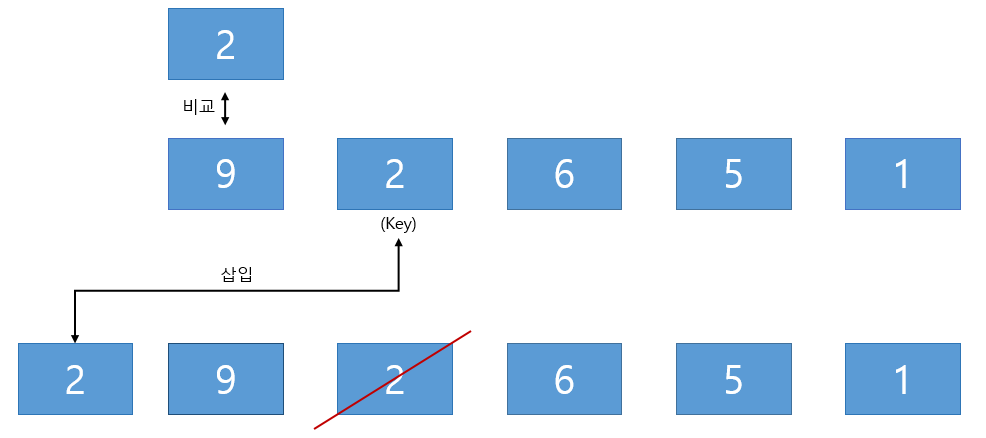
정의 : 삽입 정렬은 두번째 원소부터 시작하여 그 앞의 원소들과 비교하여 삽입할 위치를 지정하고, 원소를 뒤로 옮기고 지정 자리에 자료를 삽입하는 정렬 알고리즘이다.
-
삽입 정렬 방법 (오름차순)
- 정렬이 되지 않은 배열의 1번 인덱스의 key로 선택
- 선택한 key보다 낮은 인덱스 위치의 요소와 key 인덱스의 요소 비교
- key 요소가 들어갈 위치에 삽입
- key++
[2~4번 반복한다.]
-
특징
- 배열 내에서 교환하는 방식이므로 공간 복잡도는 O(1) 이다.
- 임시 변수 정도의 추가 공간만 필요하므로 in-place 정렬이다.
- 삽입 정렬은 중복된 키 값의 순서가 정렬 후에도 유지되므로 stable 정렬이다.
- 시간 복잡도는 O(n^2) 이다.
- 선택 정렬이나 버블 정렬에 비해 상대적 빠르다
-
구현 코드
class Sort { public void insertionSortAsc(int[] arr) { //오름차순 for (int i = 1; i < arr.length; i++) { int j = i; while (j > 0 && arr[j - 1] > arr[j]) { swap(arr, j - 1, j); j--; } } } public void insertionSortDesc(int[] arr) { //내림차순 for (int i = 1; i < arr.length; i++) { int j = i; while (j > 0 && arr[j - 1] < arr[j]) { swap(arr, j - 1, j); j--; } } } public void swap(int[] arr, int index1, int index2) { int temp = arr[index1]; arr[index1] = arr[index2]; arr[index2] = temp; } }
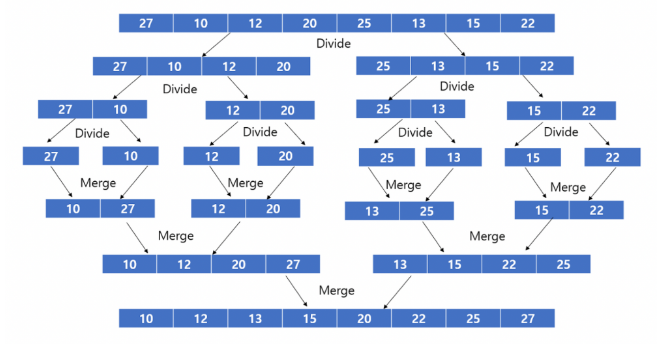
병합 정렬 (Merge sort)

-
정의 : 병합 정렬은 분할 정복의 대표적인 예로, n개의 데이터를 가진 배열을 오름 차순으로 정렬하기 위해 병합정렬 사용시 아래와 같은 3단계 과정을 거치게 된다.
- 과정
- Divide(분할) : n개의 원소를 갖는 배열을 n/2 개의 원소를 갖는 작은 배열 2개로 나눈다.
- Conquer(정복) : 각 작은 배열을 정렬한다.
- Combine(병합) : 정렬된 작은 배열들을 병합한다.
- 과정
-
분할 정복(divide and conquer)
- 정의 : 문제를 작은 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
-
병합 정렬 방법
- 특징
- 병합 정렬은 분할한 작은 배열을 위한 저장공간이 따로 필요하기 때문에 n개의 원소를 n/2 개씩 나누어 병합 정렬의 공간 복잡도는 O(n) 이다.
- 병합 정렬은 중복된 키 값의 순서가 정렬 후에도 유지되기에 stable 정렬이다.
- 분할한 작은 배열을 위한 분할한 작은 배열을 위한 저장공간이 따로 필요하기 때문저장공간이 따로 필요하기 때문에 not-in place 정렬이다.
- 시간 복잡도는 O(nlogn) 이다.
-
구현 코드
class Sort { public void ascMergeSort(int[] arr) { ascSort(arr, 0, arr.length); } public void descMergeSort(int[] arr) { descSort(arr, 0, arr.length); } private static void ascSort(int[] arr, int low, int high) { if (high - low < 2) { return; } int mid = (low + high) / 2; ascSort(arr, 0, mid); ascSort(arr, mid, high); ascMerge(arr, low, mid, high); } private static void descSort(int[] arr, int low, int high) { if (high - low < 2) { return; } int mid = (low + high) / 2; descSort(arr, 0, mid); descSort(arr, mid, high); descMerge(arr, low, mid, high); } private static void ascMerge(int[] arr, int low, int mid, int high) { int[] temp = new int[high - low]; int t = 0, l = low, h = mid; while (l < mid && h < high) { if (arr[l] > arr[h]) { temp[t++] = arr[l++]; } else { temp[t++] = arr[h++]; } } while (l < mid) { temp[t++] = arr[l++]; } while (h < high) { temp[t++] = arr[h++]; } for (int i = low; i < high; i++) { arr[i] = temp[i - low]; } } private static void descMerge(int[] arr, int low, int mid, int high) { int[] temp = new int[high - low]; int t = 0, l = low, h = mid; while (l < mid && h < high) { if (arr[l] < arr[h]) { temp[t++] = arr[l++]; } else { temp[t++] = arr[h++]; } } while (l < mid) { temp[t++] = arr[l++]; } while (h < high) { temp[t++] = arr[h++]; } for (int i = low; i < high; i++) { arr[i] = temp[i - low]; } } }
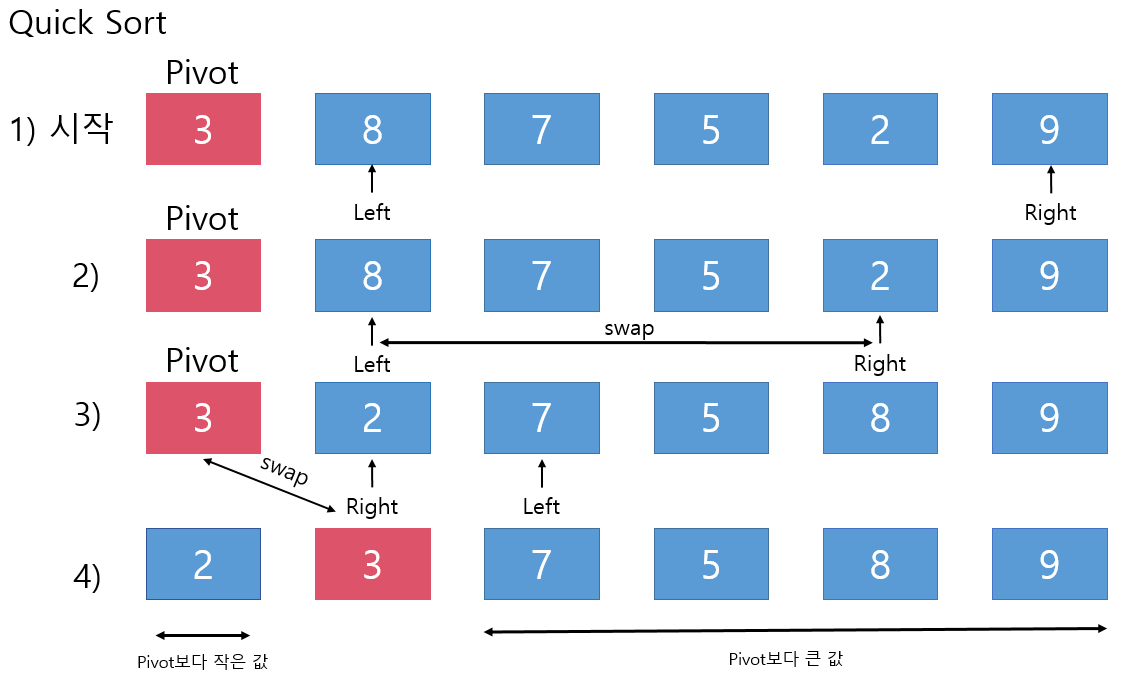
퀵 정렬 (Quick Sort)
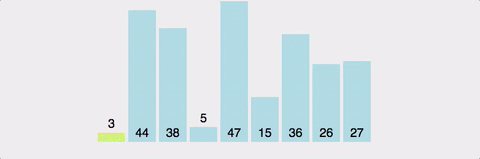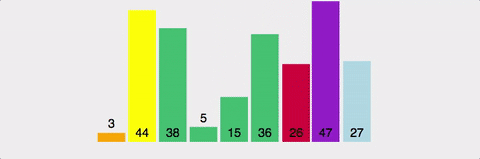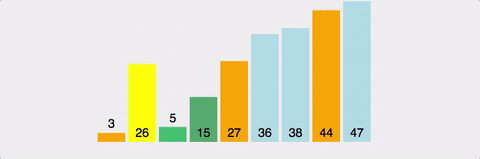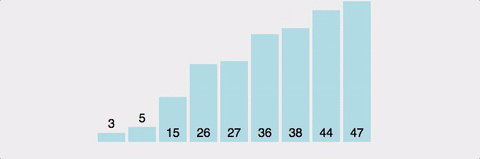
- 정의 : 퀵 정렬은 병합 정렬과 비슷하게 분할정복(Divide and Conquer) 알고리즘 하나로 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법
-
퀵 정렬 방법
-
정렬이 되지 않은 배열의 1번 인덱스를 pivot으로 선택, pivot 다음 인덱스를 Left로 선택, 마지막 인덱스를 Right으로 선택
-
각 조건에 맞을때 까지 Left, Right 증감
- Left 인덱스의 요소가 pivot보다 클때까지 Left++
- Right 인덱스의 요소가 pivot보다 작을때까지 Right++
-
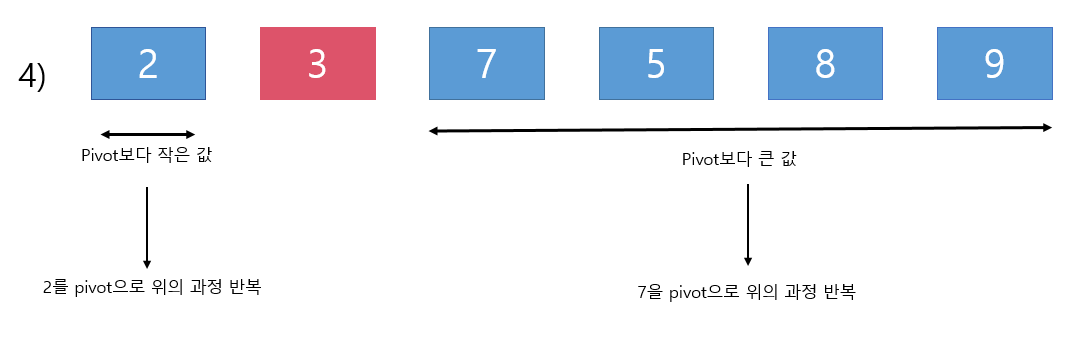
Left와 Right 변수의 크기 비교 후 swap
- Left <= Right 일 경우(
arr[Left]← swap →arr[Right]) - Left > Right 일 경우 (
arr[pivot]← swap →arr[Right])
- Left <= Right 일 경우(
[ pivot 기준 좌우측의 첫번째 요소를 pivot으로 2~4번 반복한다.]
-
-
특징
-
퀵정렬은 재귀적으로 정의되므로 재귀 호출에 따른 스택이 사용된다. 이때 스택의 깊이는 n개의 원소에 대해 logn에 비례하므로 공간복잡도는 O(nlogn)이다.
⇒ 따라서 in-place 정렬이라고 하기 힘들지만, 실용적으로는 상대적으로 작은 메모리만을 사용하므로 흔히 in-place 정렬이라고 기술하기도 한다.
-
퀵정렬은 최악의 경우 pivot이 배열 내에서 가장 작은 값 또는 가장 큰 값으로 설정된다면 원소 n개에 대해서 n번, (n-1)번, (n-2)번...n번 의 비교가 필요하므로 시간 복잡도가 O(n^2)된다.
-
하지만 평균 시간 복잡도는 O(nlogn)으로 매우 빠르다.
⇒ pivot 값이 적절히 설정된다면 그 속도가 매우 빠르기 때문에pivot값을 잘 설정하는 것이 중요하다. -
퀵 정렬은 중복된 키값이 순서대로 바뀌지 않을 수 있기 때문에 not-stable 정렬 이다.
ex) {7,7,1}을 오름차순으로 퀵정렬의 경우
-
-
구현 코드
class Sort { public void quickSortAsc(int[] arr, int first, int last) { if (first >= last) return; int pivot = first; int left = first + 1; int right = last; while (left <= right) { while (left <= last && arr[left] <= arr[pivot]) { left++; } while (right > first && arr[right] >= arr[pivot]) { right--; } if (left > right) { swap(arr, pivot, right); } else { swap(arr, left, right); } } quickSortAsc(arr, first, right - 1); quickSortAsc(arr, right + 1, last); } public void quickSortDesc(int[] arr, int first, int last) { if (first >= last) return; int pivot = first; int left = first + 1; int right = last; while (left <= right) { while (left <= last && arr[left] >= arr[pivot]) { left++; } while (right > first && arr[right] <= arr[pivot]) { right--; } if (left > right) { swap(arr, pivot, right); } else { swap(arr, left, right); } } quickSortDesc(arr, first, right - 1); quickSortDesc(arr, right + 1, last); } public void swap(int[] arr, int index1, int index2) { int temp = arr[index1]; arr[index1] = arr[index2]; arr[index2] = temp; } }
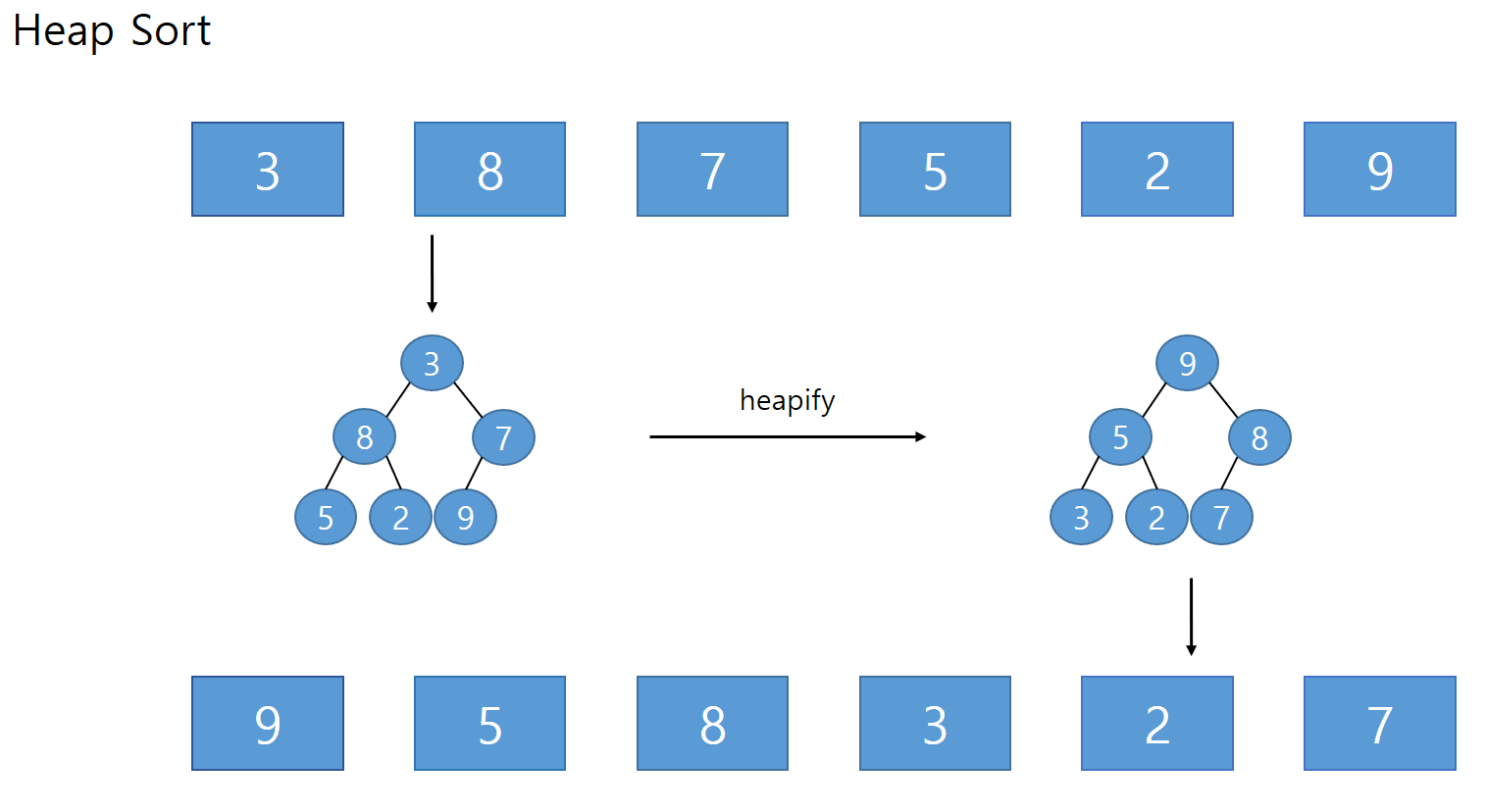
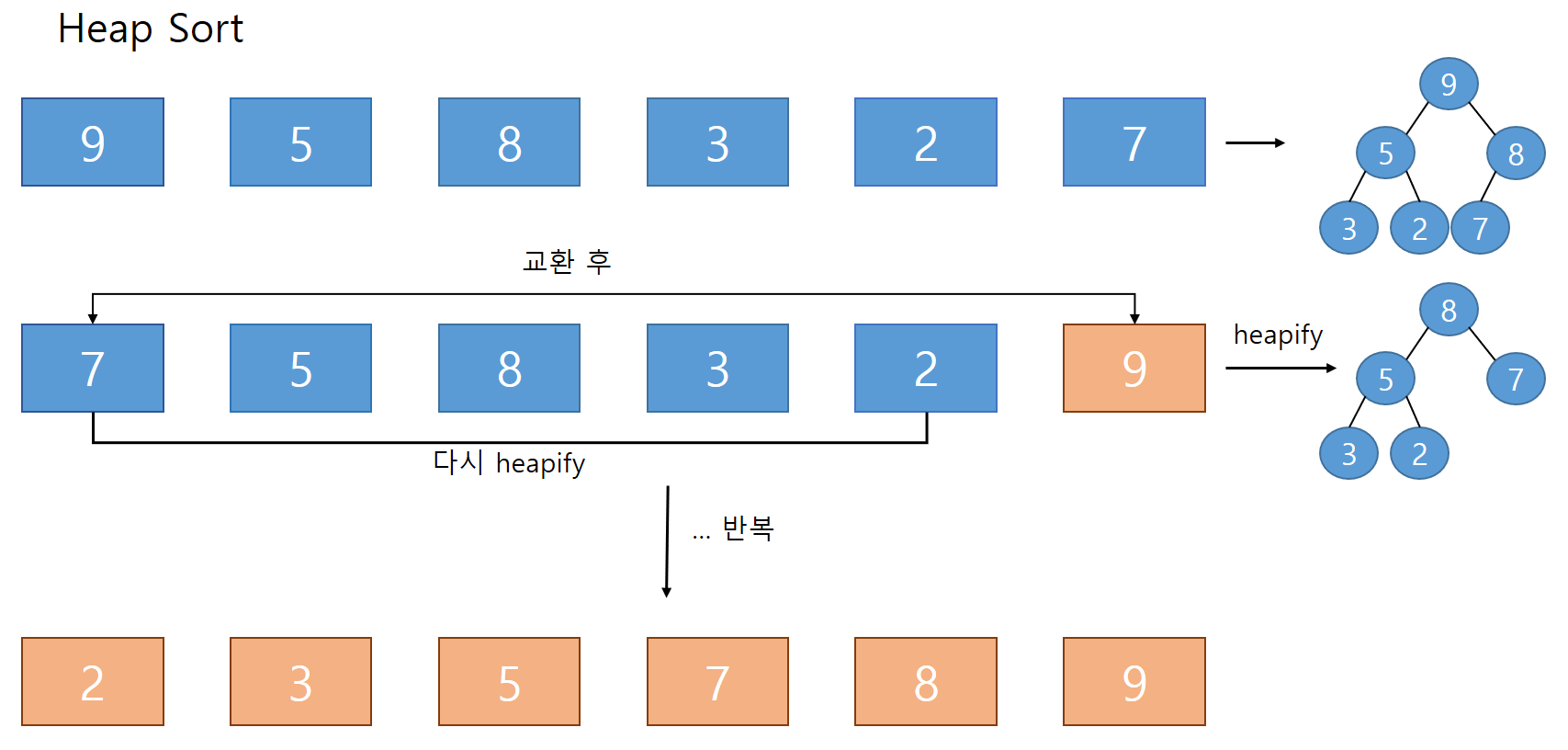
힙 정렬 (Heap Sort)

- 정의 : 완전 이진 트리의 일종인 Heap 자료구조를 구성하고 root의 원소를 하나씩 빼내어
-
heap 정렬 방법
-
정렬이 되지 않은 배열을 heapify를 통해 재구성
-
재구성한 배열의 첫번째 요소를 마지막 인덱스로 옮긴 후 마지막 요소 제외하고 다시 heapify를 통해 재구성
[마지막 인덱스부터 역으로 첫번째 요소와 교체해가며 2번 반복]
-
-
특징
-
Heap sort는 추가적인 메모리를 사용하지 않고 하나의 array로 sorting을 하기 때문에 in-place 정렬이다.
-
Heapify를 통해 위치가 변경되기 때문에 not stable 하다.
-
시간복잡도는 O(nlogn)이다.
-
시간 복잡도는 데이터를 넣을 때도 O(logN)이고 뺄 때도 O(logN)이라 고른 성능을 보인다.
-
N개의 데이터를 모두 빼면 정렬이 되기 때문에 힙 정렬의 시간 복잡도는 O(nlogn)이 된다.
-
-
-
구현 코드
class Sort { public void ascHeapSort(int[] arr) { maxHeapfiy(arr, arr.length); for (int i = arr.length - 1; i > 0; i--) { swap(arr, 0, i); maxHeapfiy(arr, i); } } public void descHeapSort(int[] arr) { minHeapfiy(arr, arr.length); for (int i = arr.length - 1; i > 0; i--) { swap(arr, 0, i); minHeapfiy(arr, i); } } private void maxHeapfiy(int[] arr, int last) { for (int j = 1; j < last; j++) { int child = j; while (child > 0) { int parent = (child - 1) / 2; if (arr[child] > arr[parent]) { swap(arr, parent, child); } child = parent; } } } private void minHeapfiy(int[] arr, int last) { for (int j = 1; j < last; j++) { int child = j; while (child > 0) { int parent = (child - 1) / 2; if (arr[child] < arr[parent]) { swap(arr, parent, child); } child = parent; } } } private void swap(int[] arr, int index1, int index2) { int temp = arr[index1]; arr[index1] = arr[index2]; arr[index2] = temp; } }
알고리즘 분석 종합
| Algorithm | Best | Avg | Worst | in-place | stable |
|---|---|---|---|---|---|
| 선택정렬(Selection Sort) | O(n^2) | O(n^2) | O(n^2) | in-place | not stable |
| 버블정렬(Bubble Sort) | O(n^2) | O(n^2) | O(n^2) | in-place | stable |
| 삽입정렬(Insertion Sort) | O(n) | O(n^2) | O(n^2) | in-place | stable |
| 병합정렬(Merge Sort) | O(nlogn) | O(nlogn) | O(nlogn) | not in-place | stable |
| 퀵정렬(Quick Sort) | O(nlogn) | O(nlogn) | O(n^2) | in-place | not stable |
| 힙정렬(Heap Sort) | O(nlogn) | O(nlogn) | O(nlogn) | in-place | not stable |