문제 풀이 아이디어
😅 완전 탐색
처음에 문제를 읽자마자 바로 손 가는대로 풀면 아래와 같은 코드가 됩니다. skill에 주어진 범위를 전부 순회하면서 일일히 데미지 혹은 힐량을 누적하고 마지막에 파괴되지 않는 건물을 세는 방법입니다.
아주 직관적인 방법이지만 정확성 테스트를 통과할 뿐, 효율성 테스트는 전혀 통과할 수 없습니다. 행의 길이(N) 최대 1,000이고 열의 길이(M)는 최대 1,000입니다. 그리고 skill의 길이(S)는 최대 250,000입니다. 그런데 아래 코드는 O(SNM)입니다. 그렇게 되면 연산의 횟수가 2천5백억(?!)회입니다.
func solution(_ board:[[Int]], _ skill:[[Int]]) -> Int {
var board = board
// R x C를 모두 순회하면서 데미지 or 치료 기록
for s in skill {
let t = s[0], r1 = s[1], c1 = s[2], r2 = s[3], c2 = s[4], d = s[5]
if t == 1 {
for r in r1...r2 {
for c in c1...c2 {
board[r][c] -= d
}
}
} else {
for r in r1...r2 {
for c in c1...c2 {
board[r][c] += d
}
}
}
}
var ans = 0
// 완전탐색하면서 살아남은 건물 세기
for r in 0..<board.count {
for c in 0..<board[0].count {
if board[r][c] > 0 { ans += 1 }
}
}
return ans
}누적합
현재 O(SNM)의 시간복잡도를 줄여야 합니다. 일단 skill을 순회하는 부분은 줄일 수 없습니다. 무조건 1번 순회하면서 데미지 또는 힐량을 기록해야 하기 때문입니다. 그렇다면 O(N*M) 부분을 줄이는 수 밖에 없습니다. 이 포스팅에서 소개한 누적합이라는 기법을 사용하도록 하겠습니다.
누적합은 배열의 일정한 범위에 원하는 값을 모두 더하려고 할 때 해당 범위를 순회하는 것이 아니라 시작점과 (끝나는 점 + 1)에 표시를 해두고 마지막에 1번만 배열을 순회하면서 값을 실제로 반영하는 방법입니다. 누적합을 활용하면 O(N*M)의 시간복잡도를 O(1)로 줄일 수 있습니다.
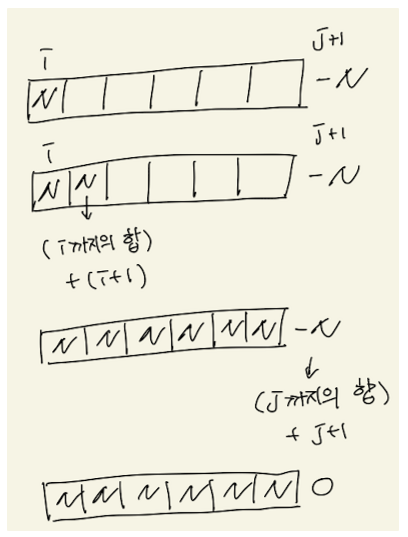
누적합을 그림으로 설명하면 아래와 같습니다. i ~ j까지의 index에 N만큼 더하는 방법입니다. i ~ j까지 순회하면서 모든 index에 값을 더하는 것이 아니라 i에 N, j + 1에 -N을 더해놓습니다. 모든 누적합을 표시하고 나면 마지막에 1번만 순회하면서 누적합을 계산하면 됩니다.
i + 1 = (i까지의 누적합) + (i + 1)입니다. 이렇게 하면 i에서 j까지 N을 더할 수 있고 마지막에 j + 1의 -N의 경우 0으로 상쇄되므로 원하는 범위인 i ~ j에 N만큼 더할 수 있습니다.
아래 예시는 1번만 누적합을 표시해서 별 감흥(?)이 없지만 문제처럼 250,000의 누적합을 표시한다면 성능을 엄청나게 향상할 수 있습니다. 250,000번 동안 매번 NM번의 연산을 실행해야 하는 것을 단 1번의 NM 연산으로 막을 수 있습니다. 즉 시간복잡도가 O(SNM)에서 O(S + N*M), 즉 O(S)가 되는 것이죠.
2차원 누적합
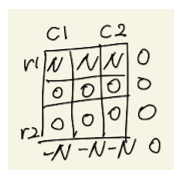
누적합이라는 방법을 찾았지만 아직 문제가 100% 해결된 것은 아닙니다. 위의 예시는 1차원 배열입니다. 하지만 문제는 2차원 배열에서 누적합을 구해야 합니다. 열의 길이가 M이므로 1차원 누적합을 M번 실행하면 2차원 누적합이 됩니다. (아래 그림 참고) 그리고 나서 각열에 대해서 누적합 연산을 하면 원하는 결과를 얻을 수 있습니다. 하지만 그러면 다시 시간복잡도가 O(S*N)이 됩니다. skill마다 각 열을 순회하면서 누적합을 표시해야 하기 때문입니다.
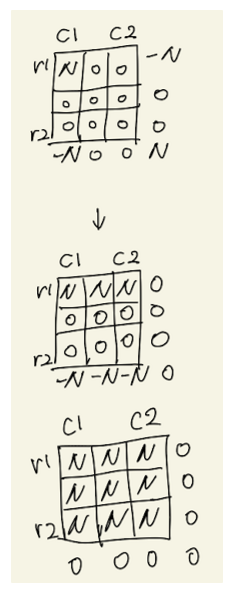
다행히 기존의 목표였던 O(S)로 풀 수 있는 방식이 있습니다. 각행을 순회하면서 위 그림과 같은 중간 누적합을 만들고 다시 각열을 순회하면서 누적합 연산을 하는 방법입니다. 아래 그림을 보도록 하겠습니다.
skill을 순회하면서 첫번째 그림처럼 표시를 합니다. 모든 표시가 끝나고 나면 각 행을 기준으로 누적합을 연산해서 기록합니다 “(r,c + 1) = (r, c)까지의 누적합 + (r, c + 1)”의 연산을 해서요. 그렇게 연산하면 위의 그림과 동일하게 열 기준으로 누적합 연산을 할 수 있게 됩니다. 열기준의 누적합 연산, 즉 “(r + 1, c) = (r, c)까지의 누적합 + (r + 1, c)”를 해서 구하면 원하는 결과를 얻을 수 있습니다.
코드
위의 2차원 누적합의 기법을 사용해서 구현한 코드는 아래와 같습니다.
func solution(_ board:[[Int]], _ skill:[[Int]]) -> Int {
var ps = Array(repeating: Array(repeating: 0, count: board[0].count + 1), count: board.count + 1)
// 누적합 표시
for s in skill {
let t = s[0], r1 = s[1], c1 = s[2], r2 = s[3], c2 = s[4], d = s[5]
ps[r1][c1] += t == 1 ? -d : d
ps[r1][c2 + 1] += t == 1 ? d : -d
ps[r2 + 1][c1] += t == 1 ? d : -d
ps[r2 + 1][c2 + 1] += t == 1 ? -d : d
}
// 행 기준 누적합 연산
for i in 0..<(ps.count - 1) {
for j in 0..<(ps[0].count - 1) {
ps[i][j + 1] += ps[i][j]
}
}
// 열 기준 누적합 연산
for j in 0..<(ps[0].count - 1) {
for i in 0..<(ps.count - 1) {
ps[i + 1][j] += ps[i][j]
}
}
var board = board
var ans = 0
// 누적합 연산 결과를 board에 반영
for i in 0..<board.count {
for j in 0..<board[0].count {
board[i][j] += ps[i][j]
if board[i][j] > 0 { ans += 1 }
}
}
return ans
}