1003번: 피보나치 함수

문제 풀이 아이디어

1. 초기값은 각각 f(0) = (1, 0), f(1) = (0, 1)입니다.
2. 점화식은 피보나치 수열과 동일하게 f(n) = f(n - 2) + f(n - 1)입니다.
	원리는 f(n)을 구할 때 f(n - 2)가 1번, f(n - 1)이 1번 실행됩니다.
	따라서 f(n - 2)할 때 실행되는 f(0)과 f(1)의 실행횟수와
	f(n - 1)할 때 실행되는 f(0)과 f(1)의 실행횟수를 각각 더해주기만 하면 됩니다.
3. 그림으로 설명하면 아래와 같습니다.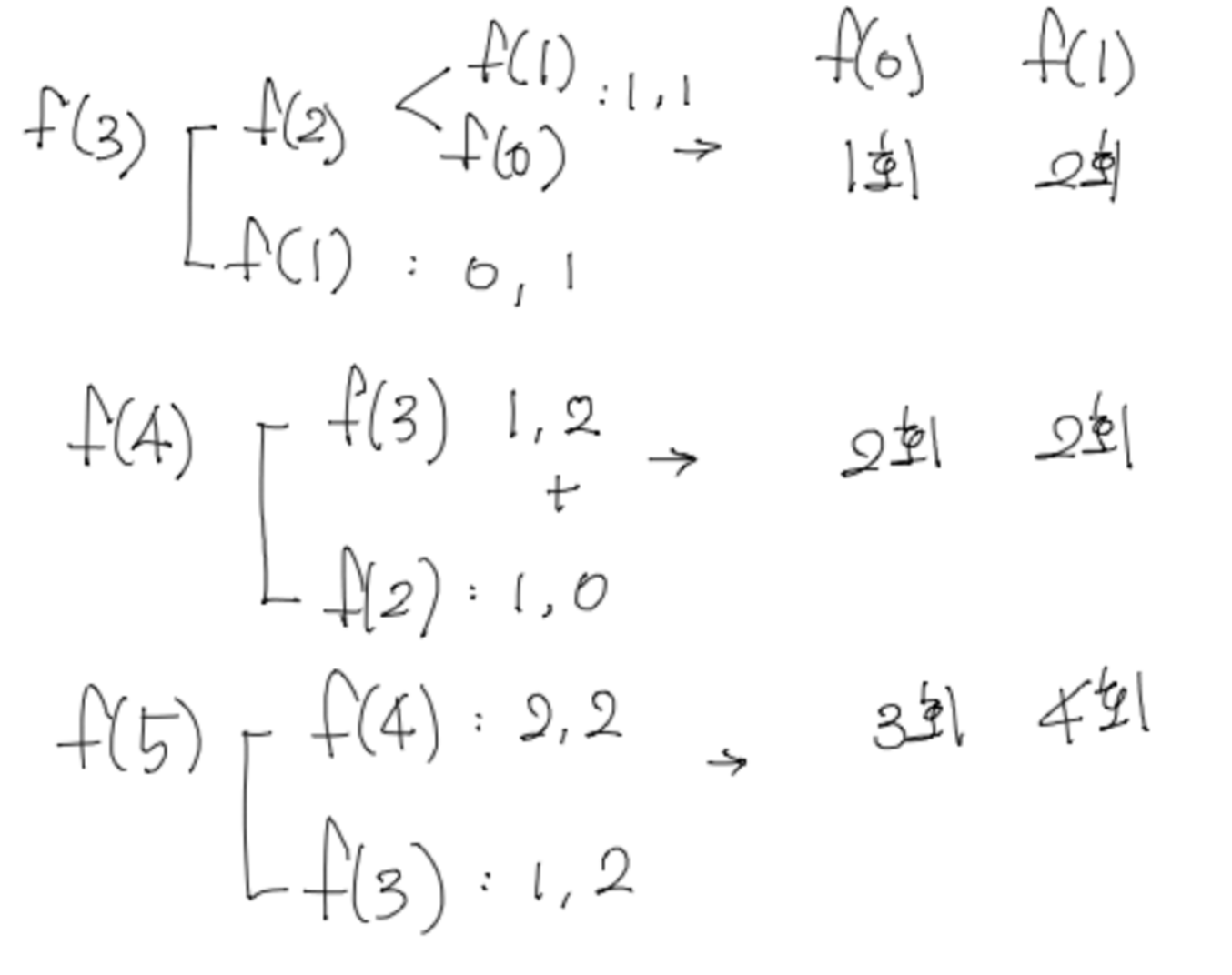

코드

반복문을 사용한 방법

반복문을 사용해서 N의 최댓값인 40까지 일단 모든 값을 구해두고 출력만 하는 방법입니다.

// 피보나치 함수
var cache = Array(repeating: (-1, -1), count: 41)

for n in 0...40 {
		// 초기 값
    if n == 0 {
        cache[0] = (1, 0)
    } else if n == 1 {
        cache[1] = (0, 1)
    } else { //👉 점화식
        cache[n] = (cache[n - 2].0 + cache[n - 1].0, cache[n - 2].1 + cache[n - 1].1)
    }
}

let T = Int(readLine()!)!

for _ in 0..<T {
    let N = Int(readLine()!)!
    print(cache[N].0, cache[N].1)
}

재귀함수를 활용한 방법

// 피보나치 함수
var cache = Array(repeating: (-1, -1), count: 41)

func f(_ n: Int) -> (Int, Int) {
    // 초기 값
    if n == 0 {
        cache[n] = (1, 0)
    } else if n == 1 {
        cache[n] = (0, 1)
    }
    // 점화식
    if cache[n].0 < 0 {
        cache[n] = (f(n - 2).0 + f(n - 1).0, f(n - 2).1 + f(n - 1).1)
    }
    
    return cache[n]
}

let T = Int(readLine()!)!

for _ in 0..<T {
    let N = Int(readLine()!)!
    print(f(N).0, f(N).1)
}