2293번: 동전 1

문제 풀이 아이디어

1. 정의
    f(i) = i원을 n가지 동전으로 나타낼 수 있는 경우의 수
2. 구하는 답
    f(k)
3. 초기값
    f(0) = 1
4. 점화식
    for coin in coins {
        f(i) += f(i - coin)
		}

처음에 푼 코드

코드

let input = readLine()!.split(separator: " ").map { Int(String($0))! }
let n = input[0], k = input[1]

var cache = Array(repeating: 0, count: k + 1)
var check = Array(repeating: false, count: k + 1)
var coins = [Int]()

for _ in 0..<n {
    let coin = Int(readLine()!)!
    coins.append(coin)
}

cache[0] = 1

for i in 1...k {
    for coin in coins {
        if i - coin >= 0 {
            cache[i] += cache[i - coin]
        }
    }
}

print(cache[k])

틀린 이유

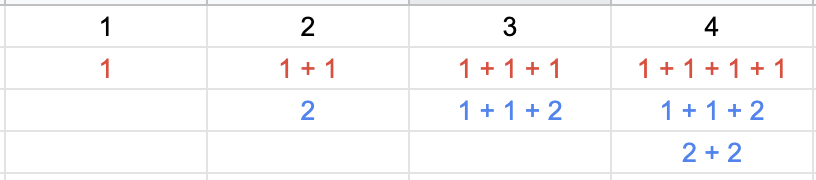
아래 화면은 i를 순서대로 3가지 동전을 순환하면서 채웠을 때 1 ~ 4까지의 경우의 수를 모두 적은 것입니다. 이렇게 i를 순서대로 채우는 경우 동전을 더하는 순서가 달라지면 다른 경우로 중복 계산이 됩니다. 마치 dfs 완전 탐색과 같은 원리입니다.

올바른 풀이

코드

// 동전 1

let input = readLine()!.split(separator: " ").map { Int(String($0))! }
let n = input[0], k = input[1]

var cache = Array(repeating: 0, count: k + 1)
var check = Array(repeating: false, count: k + 1)
var coins = [Int]()

for _ in 0..<n {
    let coin = Int(readLine()!)!
    coins.append(coin)
}

cache[0] = 1

for coin in coins {
    for i in coin...k {
        if i - coin >= 0 {
            cache[i] += cache[i - coin]
        }
    }
}

print(cache[k])

과정

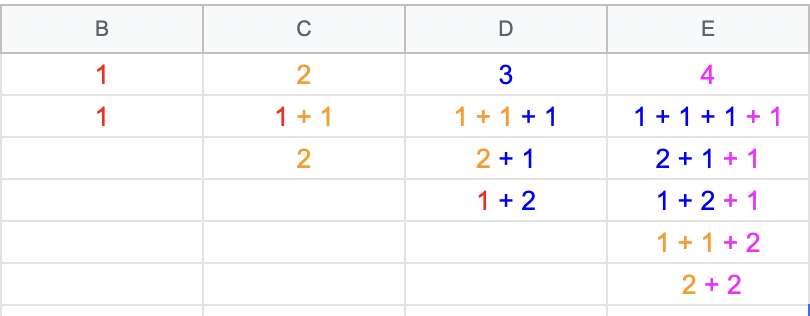
그렇다면 중복을 제거하기 위해서는 어떻게 해야할까요?

각 동전을 순회하면서 먼저 1원짜리 동전으로 구할 수 있는 경우(빨간색)를 먼저 구하고 2원(파란색), 5원짜리 동전으로 구할 수 있는 수를 구할 수 있는 경우의 수를 구하는 경우 아래와 같이 중복되는 경우의 수를 제거할 수 있습니다.