배우면서 쓰는 암호학

사실 DES는 AES 이전의 암호학이다. 현재는 DES에 대한 공격기법들이 너무나 많이 생겨나 DES 암호화 기법을 쓰지 않는다. 그럼에도 불구하고 DES를 나중에 포스팅한 이유는 .. DES가 더 복잡하고 어렵기 때문이다.

DES는 AES와 다르게 Key 가 56 bit, 평문이 64bit를 이룬다.

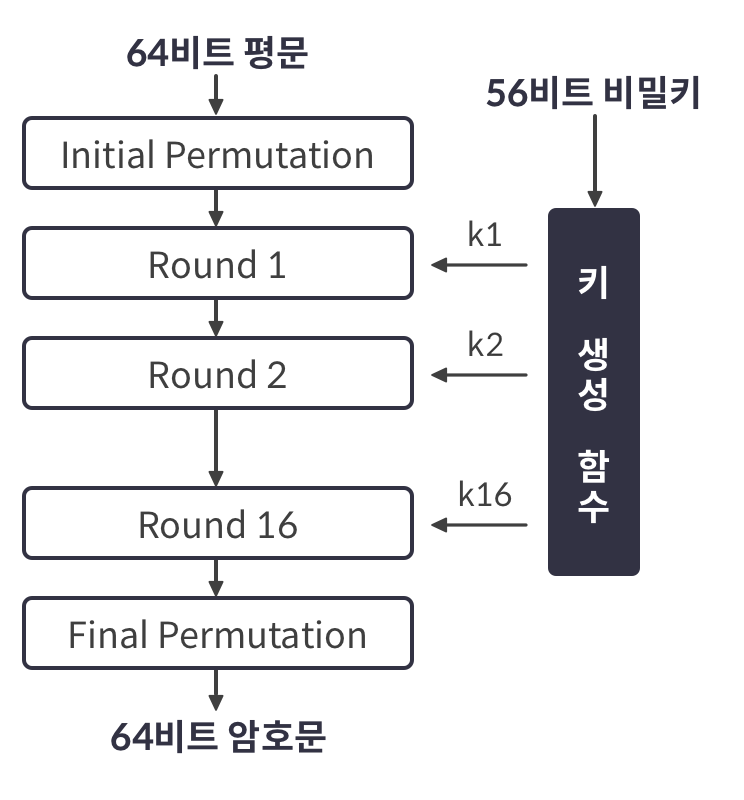
DES의 전체 구조는 위의 그림과 같이 초기 순열(Initial Permutation), 최종 순열(Final Permutation), 페이스텔(Feistel) 구조의 16 라운드, 그리고 각 라운드에 사용되는 48비트의 키를 생성하는 키 생성 함수(Key Generation)로 구성되어 있다.

그럼, DES의 원리부터 알아가보도록 하자.

- DES의 원리 -

DES는 현대 암호의 성질인 혼돈, 확산을 만족하기 위해서 치환과 순열의 암호화 방식을 사용한다.
물론 치환을 한다고 해서 혼돈을 만족하는 것은 아니고, 순열을 바꾼다고 해서 확산을 만족하지는 않지만 이 치환과 순열이라는 두 암호화 방식을 교차로 반복적으로 실행 하다 보면, 혼돈과 확산을 만족하게 된다.

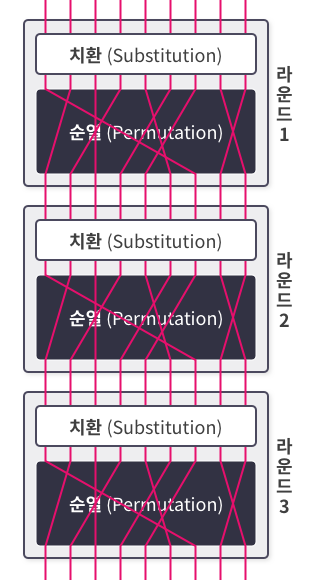
이렇게 교차로 반복 실행하는 암호화 방식을 곱 암호 (Product Cipher) 이라고 한다.
이런 곱 암호를 이용해서 DES는 Feistel 구조를 이루고 있는데, 이 구조에 대해서 알아보도록 하자.

>> Feistel Structure

Feistel 구조는 많은 암호화 시스템에서 사용하는 구조이다. 이 Feistel 구조는 특이하게 블럭을 2개로 나누어 암호화를 진행하게 된다. Feistel 구조를 그림으로 확인해 보자

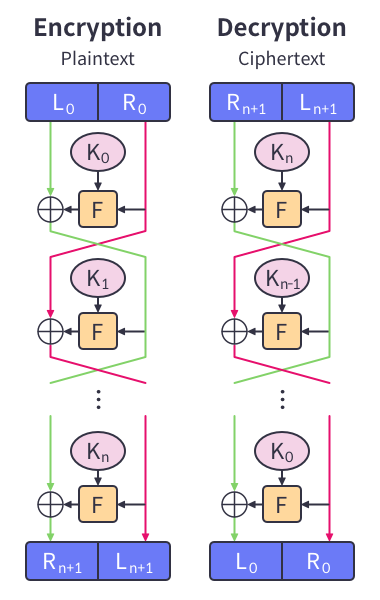
이렇게 2가지 구역인 L,R 구역으로 나우어 독립적으로 암호화를 진행하게 된다. 엄밀하게 말하면 독립적이진 않지만, 결국 결론은 L과 R 따로 나오게 된다. 이 구조의 과정을 한번 살펴보자.

1. 입력으로 들어온 블록을 동일한 길이의 왼쪽 블록 L과 오른쪽 블록 R로 구분한다.

2. 각 라운드마다 오른쪽 블록은 다음 라운드의 왼쪽 블록으로 입력됩니다.

3. 왼쪽 블록은 오른쪽 블록에 라운드 함수 F를 적용한 결과와 XOR되어 다음 라운드의 오른쪽 블록으로 입력된다.

이를 위의 그림에서 나온 수식으로 다시 설명해보면,

• L(n+1) = R(n)
• R(n+1) = L(n) ⊕ f(R(n),K(n))

와 같이 나타낼 수 있겠다.

이런 Feistel 구조에는 신기한 특징이 하나 존재한다. 바로, 역함수가 존재하지 않아도 된다는 것이다.
이게 무슨 말인가 하면, 평문을 암호화하는 함수는 항상 역함수가 존재하지는 않는다. 같은 문자를 암호화해도 다른 문자가 나올 수 있고, 다른 문자를 암호화해도 같은 문자가 나오는 '혼돈' 성질을 만족하기 때문에 함수들이 항상 일대일 대응을 만족하지는 않는다.

따라서, 암호화 함수를 안다고 해서 역함수로 복호화할 수 없다는 이야기가 된다.

그런데, 왜 이 Feistel 구조는 역함수가 없어도 복호화가 되는 것일까?? 바로 XOR 연산 때문이다. XOR 연산을 한 수식에다가 다시 또 XOR 연산을 하게 되면 원래 값으로 돌아오게 된다. 이 뜻은, 암호문을 Key의 순서만 역순으로 바꾸어 암호화해준다면 이 암호화가 복호화하는 방식이 된다는 뜻이다.

- DES 과정 -

DES 과정은 크게 3 step으로 나누어서 설명할 수 있겠다.
1,3 step은 순열, 그리고 2 step은 치환이라는 암호화 방식을 사용한다.
먼저, 1,3 step부터 알아보도록 하자.

>> 1,3 step - 순열

순열은 다른 말로 전치라고 할 수 있다. 64비트를 입력하고, 비트 단위로 전치를 하게 되는데, n번째 값이 m일 때, 출력의 n번째 비트는 입력의 m번째 비트가 된다.

예를 들어서,

이런 배열이 있다고 한다면, 배열의 3번째 값이 42가 되기 때문에 입력한 비트의 42번째 비트를 3번쨰로 오게 된다. 그런데, 이 1,3 step을 같이 설명한 이유는 무엇일까??

두 step 모두 이런 전치 과정을 거치지만, 이 두 step에는 연관성이 있다. 바로, 이 두 step은 서로 역함수 라는 것이다. 중간의 2 step을 제외하고 1,3 step만 연속적으로 실행하게 되면, 원래 평문과 동일한 결과값이 나오게 된다.

다음은 위의 IPT ( Initial ) 에 대응되는 FPT ( Final ) 배열이다.

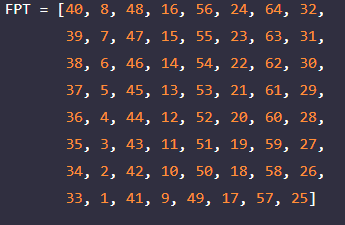
잘 보면, 아까 예시로 들었던 42번째 비트가 3번째로 오게 되는데, 여기서는 3이라는 숫자가 배열의 42번째에 위치하게 되면서 결국 3번째 비트를 42번째로 옮겨주는 시행을 하게 된다. 따라서 결국 원래 위치로 돌아가게 된다.

>> 2 step - 치환, 순열

앞서 설명했던 1,3 step과는 다르게, 2step은 3가지 과정으로 이루어져 있다.
바로 확장 순열(Expansion P-Box), 라운드 키 결합(XOR), 치환 테이블(S-Box) 그리고 고정 순열(Straight P-Box) 이다.

먼저, 확장 순열부터 설명해보도록 하자.

확장 순열

확장 순열은, 말 그대로 비트를 확장시키는 것이다.
현재 입력되는 비트의 수는 총 32 비트인데, 이를 48 비트로 늘려주는 역할을 하게 된다.

이렇게 다음과 같이 비트를 4 단위로 쪼갠 후에, 각각의 4개의 비트 단위들을 6개의 비트 단위로 확장시키게 된다. 앞서 나와 있는 그림을 보면 알겠지만, 이해를 돕기 위해 사진 하나를 첨부하도록 하겠다.

사실 확장 순열도 하나의 전치와 같다고 볼 수 있다. 이렇게 배열로 나타내게 되면, 위의 시각화 그림과 동일한 순열을 나타내고 있다는 사실을 확인할 수 있을 것이다.

라운드 키 결합

라운드 키 결합은 단순히 각 라운드에 지정된 key 배열들과, 확장 순열을 통해서 만들어진 48-bit 배열을 XOR 시키기만 하는 간단한 연산이다.

S-Box

S-Box 과정은 '확장 순열' 에서 확장했던 48-bit를 다시 원래대로 32-bit 로 바꿔주는 작업을 하게 된다.
이 과정은 마찬가지로, 48 bit를 8개의 6-bit 단위로 나누어서 진행하게 된다.

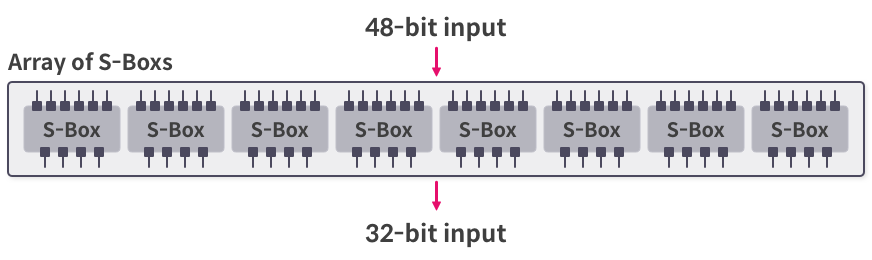
각각 단위마다 S-Box를 진행하게 되는데, 여기에 필요한 S-Box는 각 단위마다 다르다.
즉, 한번의 S-Box 과정을 수행하기 위해서는 8 개의 S-Box 가 필요하다는 말과 동치이다.

이 S-Box는 어떻게 이용해서 4개의 bit로 축소하게 될까??
이 부분은 코드를 보여주는 편이 가장 이해가 빠를 것 같기에 코드를 먼저 보여주도록 하겠다.

S-Box는 위의 배열을 사용하는데, 행이 4, 그리고 열이 16인 배열을 사용한다. 즉 2차원 배열을 사용해서, 6-bit의 수를 통해서 행과 열을 정해주게 되면, 이 행과 열에 맞는 수를 2진수로 변환해서 4 bit에 넣어주게 된다.

고정 순열

이 과정은 다른 순열 과정들과 동일한 작업을 통해서 이루어진다.
1,3 step과 마찬가지로, 일련의 배열을 토대로 원소들의 순서를 재배열하는 과정이다.

>> Key Schedule

키 생성 함수는 64 비트의 배열을 입력받아 각 라운드 함수에 필요한 48-bit 키를 16개 만들어내게 된다.
이 과정은 패리티 비트 제거(Parity Bit Drop), 쉬프트(Shift), 압축 순열(Compression P-Box) 로 구성되어 있다.

먼저, 패리티 비트가 무엇인지 살펴보자.

Parity Bit

Parity Bit는 8 비트에서 가장 마지막에 있는 비트를 말한다. 이 비트는 사실 데이터에서 정보로써 사용되는 비트가 아니다. 그렇다면 과연 이 비트는 어떤 역할을 하게 될까?

Parity Bit, 즉 8비트씩 나누었을 때 끝에 있는 bit는 앞의 7개의 비트와 자신을 포함한 8개의 비트 중에서 1의 개수를 홀수개로 맞춰주기 위해서 사용되는 비트이다.

예를 들어서, 앞의 비트가 1011011이라고 해보면, 앞선 7개의 비트들 중에서 1의 개수는 5개이기 때문에 마지막 Parity Bit는 0으로 정의해줄 수 있다. 반대로, 앞의 비트가 0100100이면, 앞선 7개의 비트 중 1의 개수는 2개이기 때문에 1의 개수를 홀수개로 맞춰주기 위해 마지막 8번째 Parity Bit는 1이 되는 것이다.

이렇게 전체 64-bit를 8개의 Parity bit를 제거함으로써 56-bit로 바꿔주게 된다.

• Q . 그렇다면 과연 이 Parity Bit는 왜 필요할까??

• A . Parity Bit는 통신 중에 비트 반전이 일어나지 않았음을 보증하는 역할을 한다. 통신 중간에서 반전이 일어나게 되면 1의 개수를 이용해서 통신 중 오류가 발생했는지 여부를 판단할 수 있기에 Parity Bit를 사용하게 된다. ( 사실 여기서 의문이 들 수 있는데, 홀수 Parity 가 있고, 짝수 Parity가 있다. 더불어서 Parity Bit는 항상 앞선 7개가 아니라 8개도 가능하기에 반전 여부를 확인할 수 있다)

shift

shift는 말 그대로 bit를 일정 거리만큼 밀어주거나 당겨주는 역할을 한다.
하지만, 우리가 알고 있는 shift와는 살짝 차이가 있다.
우리가 알고 있는 shift 역할은 10110 << 2 를 하게 되면 1011000이 만들어진다. Key Schedule 에서의 쉬프트는 입력을 왼쪽 28비트와 오른쪽 28비트로 나누어 각각을 1비트나 2비트만큼 왼쪽으로 순환 쉬프트(Cyclic Shift)하는 과정이다. 1, 2, 9, 16 라운드에서는 1비트, 나머지 라운드에서는 2비트만큼 쉬프트한다.

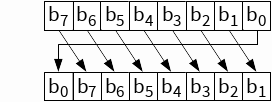
예를 들어서, 10110 << 2라는 연산을 시행하게 되면, 11010이 된다는 말이 된다. 왼쪽의 두 비트는 뒤로 가고, 나머지 비트는 앞으로 끌어와지게 된다.

Compression P-Box

이 연산은 앞서 나온 bit를 압축하는 순열인 round S-Box의 압축 과정과 동일하기 때문에 부연설명은 굳이 하지 않아도 이해하기에는 어려움이 없을 듯 하다.

이렇게 지금까지의 Key Schedule 과정을 그림으로 나타내보면 다음과 같다.

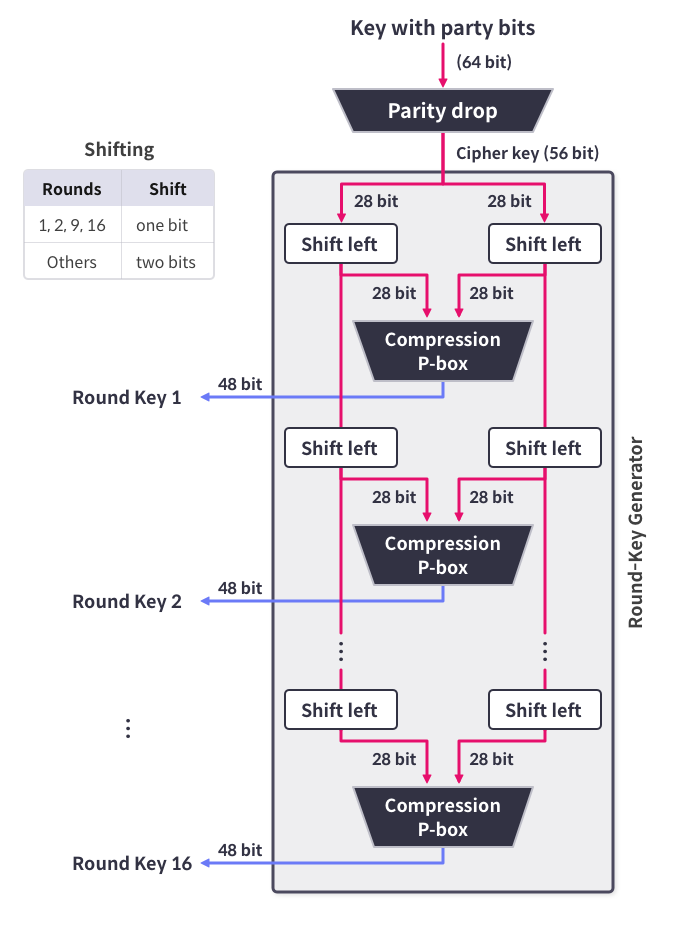
- DES의 응용 -

>> multiple DES

전에도 말했듯이, DES는 이미 많은 공격 기법들이 생겨나 더 이상 암호 체제로 사용하지 않는다. 이 문제점을 보완해주기 위해서 DES 기법을 여러번 걸쳐서 쓰는 방법이 생겨났다.

2중 DES는 DES를 2번 쓴 것으로, 112 비트를 대상으로 하고, 3중 DES는 168 비트를 대상으로 하게 된다.

이를 수식으로 타나내게 되면,

• 2중 DES : E2(E1(p))
• 3중 DES : E3(D2(E1(p)))

로 표현할 수 있게 된다. ( 여기서 D는 복호화, E는 암호화를 의미한다. )
여기서 한가지 이상한 점을 찾아낼 수 있는데, 왜 3중 DES에서는 2번째 작업이 복호화를 하게 될까?

아마 편의성을 위해서 복호화를 하게 되는 것 같은데, 왜냐하면 D2에 쓰일 key와 E3에 쓰일 key 를 같게 해주면 단일 DES 로도 쓸 수 있기 때문에 해주게 된다.

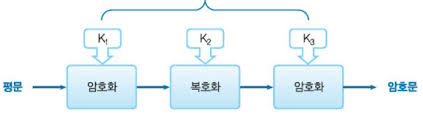
이런 식으로 DES를 하게 되면, 늘어난 Key의 길이만큼 더 안전해졌다고 생각할 수도 있겠지만, 실상은 그렇지 않다. 이중 DES는 사실 단일 DES와 비슷한 안전성을 가지고, 삼중 DES도 단일 DES 와 비교해서 2배 가까이밖에 안전성이 증가하지 않는다.

>> 중간 일치 공격

그렇다면 과연 2중, 3중 DES과 큰 효과를 가지지 못하는 이유가 무엇일까?? 바로 지금부터 설명할 중간 일치 공격의 효과 때문이다.

중간 일치 공격은 이중, 삼중 DES가 존재할 때 사용하게 되는데, 평문 P와 암호문 C를 모두 알고 있을 때 사용할 수 있다.

중간 일치 공격의 과정은 다음과 같다.

이중 DES 과정

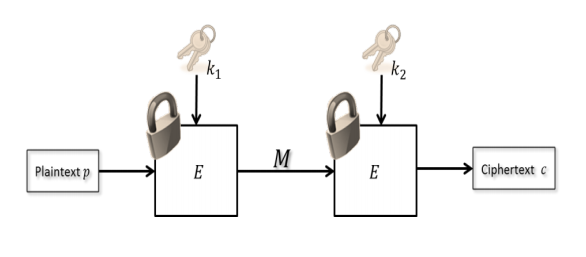
중간 일치 공격

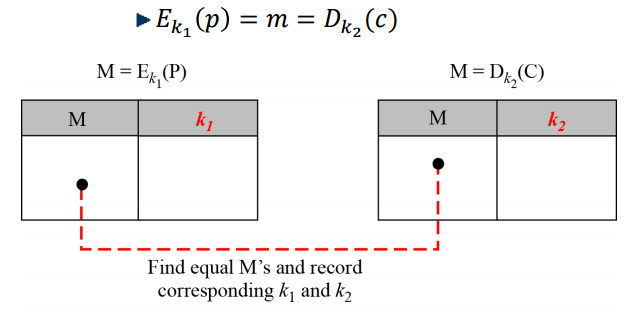
이렇게 P를 암호화 할 수 있는 모든 key를 바탕으로 E(p)들을 집합으로 만들게 된다. 마찬가지 방법으로 C를 복호화할 수 있는 모든 Key를 바탕으로 D(p)들의 집합을 만들게 되면, 항상 두 값이 일치하는 경우가 나오게 된다.

따라서 위의 그림처럼, 두 값이 일치하는 k1,k2 의 순서쌍들을 집합으로 하는 CK 집합을 만들게 되는데, 이 과정을 다른 P, C에 대해서도 반복하게 되면 결국 CK 집합의 원소가 유일하도록 특정시킬 수 있게 된다.

따라서 이중 DES나 삼중 DES의 안전성은 그다지 높아지지 않게 된다.

이 중간 일치 공격 때문에, 우리가 다중 DES를 사용할 때는 그나마 안전성이 높아지는 3중 DES를 주로 사용하게 된다.

---

여기까지가 이번 포스트에서 설명할 내용이다.
다음 포스팅에서는 운영 모드에 대해서 알아보도록 하자.