배우면서 쓰는 암호학

앞서 설명했던 AES는 128bit, DES 는 64bit를 하나의 블럭으로 인식해서 계산하는데, 이는 알파벳으로 16글자, 8글자에 해당한다. 하지만, 우리가 평소에 암호화에 사용되는 평문의 길이는 이보다 훨씬 긴 문자열들이 많다.

이번 포스팅에서는 블록 암호를 통해서 이런 다양한 크기의 데이터를 다루는 데에 필요한 운영 모드 (Mode of Operation) 에 대해서 알아보도록 하자.

- Padding -

먼저, 블록 암호에 절대적으로 필요한 과정이 있다. 바로 Padding 이다. 전의 포스트에서도 잠깐 설명했지만, Padding은 평문 뒤에 쓸모없는 데이터를 덧붙여서 블록 단위가 되도록 해주는 과정을 의미한다.

이 Padding 과정을 겪고 나면, 암호문에도 뒤에 Padding을 거친 영역이 나타나게 되는데, 복호화를 하고 난 후에는 이를 제거해야 정확한 정보를 얻을 수 있기 때문에 어떤 Padding 이 이루어졌는지를 알아야 한다.

Padding에는 총 비트 패딩(Bit Padding), 바이트 패딩(Byte Padding), 그리고 PKCS#7 패딩이 있다.

>> Bit Padding

먼저, Bit Padding 부터 알아보도록 하자.

Bit Padding은 남는 비트에 처음엔 1, 그 후에는 모두 0 으로 채워주는 방법이다.

예를 들어서, 1011 1001 1111 1100 1101 이라는 평문이 있다고 가정해보자.
이 평문을 암호화하는 방식이 32비트를 기준으로 한다고 했을 때, 12비트가 남게 된다. 따라서 이 뒤에 1000 0000 0000 이라는 비트를 붙여주어서 Padding을 완료할 수 있다.

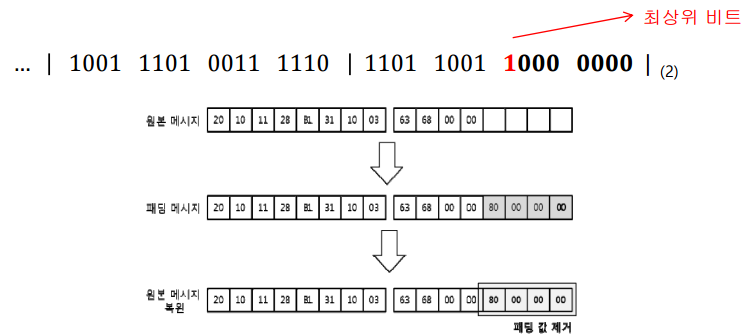
하지만, 이 비트 패딩에는 문제점이 존재한다.
바로 단위에 정확히 맞는 Bit를 입력할 시에, 패딩 범위가 아닌데도 패딩으로 인식하고 지워버릴 수도 있다.

예를 들어서, 1101 1100 1111 1000 이라는 정보가 복호화를 통해서 생겨났다고 가정할 때, 비트 패딩이 적용되었다고 감지하고 최하위 4개의 비트를 삭제할 수 있는 여지가 존재한다.

이를 막기 위해 비트 패딩을 적용할 때는 평문의 크기가 블록 크기의 배수이면, 패딩으로 한 블록을 추가하는 방법을 이용한다. 이 방법을 이용하면 앞서 들었던 예시인 1101 1100 1111 1000 이라는 블록 뒤에 하나의 블록을 더 추가하여 1101 1100 1111 1000 / 1000 0000 0000 0000라는 패딩이 이루어진다.

>> Bytes Padding - ANSI X.923

바이트 패딩 중에서도 ANSI X.923 패딩 기법은 마지막 남은 부분들을 0으로 채우고, 마지막 바이트를 잔여 바이트 수로 두는 것이다.

예를 들어서 'A3B291815023000014500000' 라는 문자열이 있다고 가정해보자. 이 문자열을 블록으로 나누어보면

• A3 B2 91 81 50 23 00 00 / 14 50 00 00 ?? ?? ?? ??

이 된다. 위에서 말했던 것처럼 그 뒤의 바이트는 모두 0 으로 만들어주고, 마지막 바이트만 잔여 바이트 수로 바꿔주게 된다. 예시의 경우에는 잔여 바이트 수가 4개 이기 때문에 결국

• A3 B2 91 81 50 23 00 00 / 14 50 00 00 00 00 00 04

로 바꿔주게 된다.
이를 ANSI X.923 Byte Padding 이라고 한다.

>> Byte Padding - PKCS#7

이 패딩은 위에서 소개한 ANSI X.923 의 패딩 기법과 유사하다. 위의 기법은 마지막 바이트만 잔여 바이트 수로 정의하고, 나머지를 0으로 채우는 방법이였는데, 이번에 소개할 방법은 모든 바이트를 잔여 바이트 수로 정의하는 것이다.

위의 예시를 그대로 가져와보면,

• A3 B2 91 81 50 23 00 00 / 14 50 00 00 04 04 04 04

로 나타낼 수 있겠다.

- mode of operation -

이번에는 블록 암호화 기법에 따라서 평문을 여러 블록들로 나누게 되는데, 이런 여러 블록들은 어떤 방식으로 암호화되는지에 대해서 알아보고자 한다.

지금까지는 블록 하나하나를 어떤 방식으로 암호화가 되는지에 대해서 알아보았다면, 이번에는 블록들 간의 암호화 방식의 차이에 대해서 서술하고자 한다.

이 방법에는 총 3가지 운영모드,

• ECB ( Electronic code book )
• CBC ( Cipher block chaining )
• CTR ( Counter )

에 대해서 알아보자.

>> ECB

ECB 운영모드는 가장 간단한 운영모드로, 모든 블록이 같은 암호화 KEY를 사용한다. 이 운영 모드에서는 같은 키를 사용하기 때문에 모든 블록을 동시에, 병렬적으로 암호화하는 것이 가능하다.

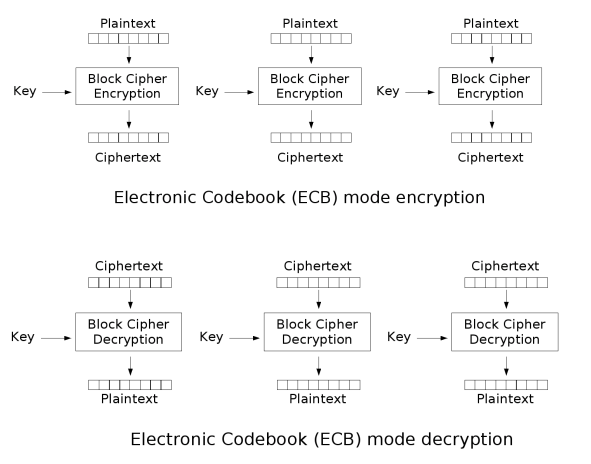
하지만 이런 단순한 특성 때문에 운영 모드의 안전성이 떨어지게 된다.

취약점

이 운영 모드는 다시 말해서 같은 암호화 모듈을 사용하기 때문에 혼돈의 성질이 미약할 수 있다. 어떤 픽셀을 암호화하게 되면, 이 픽셀들이 모두 같은 암호화 모듈로 암호화가 되기 때문에 다음과 같은 현상을 발견할 수 있다.

이렇게 하나의 이미지를 암호화할 떄, 모두 같은 KEY를 사용하기 때문에 결국 이미지도 대략 유추할 수 있게 된다.

추가로, 이를 파훼하기 위한 공격 방법인 리플레이 공격 방법이 있다.

Replay Attack

이 공격기법은 말 그대로 다시 보내 공격한다는 이야기이다.

만약, 철수가 영희에게 10000원을 보내기 위해서 은행에 '철수가 영희에게 10000원을 송금' 이라는 문자열을 전송한다고 생각해보자. 철수는 이를 암호화해서 'a1ijc1ox0fdz0d1vforca3je' 로 암호화해서 보내게 되고, 은행은 이를 해석해서 원래의 문자열로 해석해 10000원을 송금하게 된다.

그런데 여기에서, 영희가 철수가 암호화한 암호문과 평문을 모두 안다면, 이를 통해서 0000이 0d1v로 암호화되었다는 사실을 알 수 있다. 그렇다면, 이와 같은 암호문을 그냥 a1ijc1ox0fdz0d1v0d1vforca3je 뒤에 0000을 더 붙여준다면, 은행은 100000000원을 송금하는 것으로 알아들을 것이다.

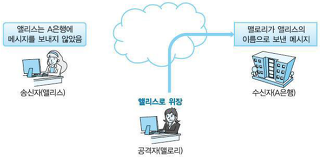
이와 같이 다시 보내서 공격하는 기법을 Replay Attack 이라고 한다.

>> CBC

다음은 CBC 운영모드이다.
CBC 운영모드에서는, 어떤 블록을 암호화하려고 할 때, 전 블록의 암호문과 현 평문을 XOR 작업을 통해서 한번 더 암호화해주게 된다. 그래서 EBC와는 달리 병렬적으로 암호화 작업이 이루어지지 않는다.

그림으로 나타내보면 다음과 같다.

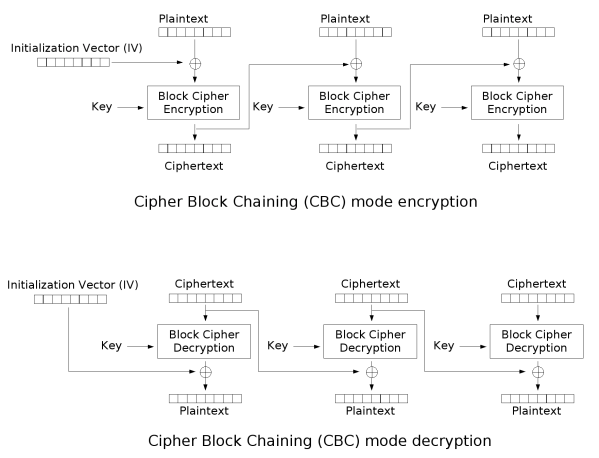
첫 블록은 전 블록이 없기 때문에 Nonce (Number used only once ) 라는 무작위의 숫자들을 이용해서 XOR에 사용해준다. 이 수는 공격자도 알고 있어도 이후의 안전성에 영향을 끼치지 않는다.

더불어서, 전 블록에 영향을 받기 때문에 EBC 같은 공격 기법과 달리 혼돈의 성질을 만족한다고 볼 수 있다.

CBC Bit-Flipping Attack

공격자가 Nonce 라는 수를 알아도 안전성에 영향을 끼치지는 않지만, 이 Nonce 값은 변경할 수 있게 된다면 이야기가 달라진다.

Nonce 값을 마음대로 변경할 수 있다면, 첫 블록의 비트도 변경시킬 수 있다는 이야기가 된다.

복호화를 할 때의 과정을 수식으로 나타내보자.

• C = E(P ⨁ IV)
• P ⨁ IV = D(C)
• P = D(C) ⨁ IV

자. 결국 이런 수식이 된다.
( 이제와서 설명하지만, P : Plaintext (평문), E : Encryption (암호화), D : Decryption (복호화), C : Ciphertext (암호문) ) 이라는 뜻이다.

그런데, 여기서 만약 IV' = P ⨁ P' ⨁ IV 의 값으로 IV를 변경시킨다면, P 를 P'으로 강제 변형시킬 수가 있다.

따라서 복호화 과정에서 이상하게 복호화가 되도록 조작할 수 있다는 것이다.

예를 들어서, '철수가 10000원을 소유함.' 이라는 문장을 암호화해서 ' asdljeijjir' 가 되었다고 했을 때, 앞의 바이트를 조작할 수 있기 때문에 '영희가 10000원을 소유함' 이라고 복호화되도록 조작할 수 있다는 것이다.

>> CTR

CTR은 counter의 약자이다. nonce와 평문 블록의 인덱스(counter)를 결합한 값을 입력합니다. 암호문은 블록 암호의 출력과 평문 블록을 XOR하여 생성합니다.

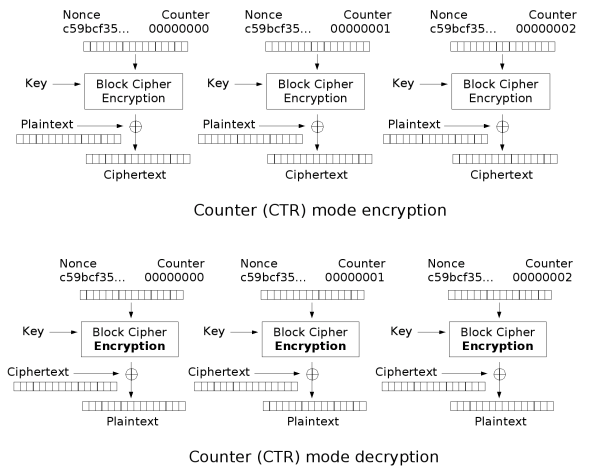
다음과 같은 방법으로 암호화, 복호화가 이루어지는데, 이해를 돕기 위해 수식으로 표현해보면,

• C = P ⨁ E( nonce || counter )

다음과 같이 나타낼 수 있다. 이 수식에서 || 기호는 nonce와 counter 을 결합해주는 연산이라고 생각하면 될 것 같다.
이 CTR 기법은 장점은 EBC와 마찬가지로 병렬적으로 실행이 가능하다는 점과, 난수가 공개되어도 기밀성에 문제가 되지 않는다는 점이다.

이런 일련의 과정들을 거쳐서, 지금까지 설명한 블록 암호화 방식이 실행되게 된다.

---