배우면서 쓰는 암호학
이번 포스팅 주제는 암호학이다. 사실 나는 암호학에 대하여 아는 것이 거의 없다.
암호학 하면 고대에 종이를 원통에 빙빙 감아서 만든 암호? 그 정도밖에 모른다.
자. 그렇다면 암호학에 대해서 같이 알아보자!!
- 고전 암호 -
고전 암호는 말 뜻 그대로 과거에 사용했던 암호 체계를 말한다.
컴퓨터와 같은 계산 장치가 발전하기 전부터 사용했던 암호로, 현대에는 비교적 쉽게 복호화 할 수 있기 때문에 현대에는 잘 사용하지 않는다.
이 고전 암호는 보통
- 치환 : 문자를 다른 문자로 변환
- 전치 : 문자들의 위치를 변환
이렇게 2가지 방법을 이용해서 만들어진다.
먼저, 치환 방법을 살펴보자.
>> 치환
이 치환 방법은 또 2가지 암호로 나누어지게 된다.
-
단일 문자 치환 암호 - 하나의 문자에 하나의 문자만 대응 ( 일대일 대응 )
-
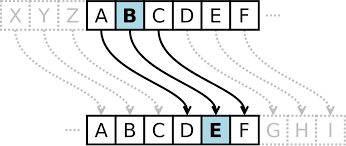
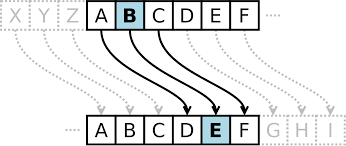
단일 문자 치환 암호은 각 문자를 다른 문자에 일대일 대응시켜서 암호화한다.
-
위의 그림은 단일 문자 치환 암호의 대표적인 예시이다. 이렇게 알파벳을 일정한 거리만큼 밀어서 다른 문자로 대응시키는 암호를 "카이사르 암호" 라고 한다.
-
이를 수식으로 표현하게 되면, x를 암호화 전 알파벳 순서, n을 카이사르 암호에서의 대응 거리라고 하면, 암호화 후의 알파벳은 f(x) ≡ x+n (mod26) 가 된다.
EX) FDAC → IGDF ( 위의 그림을 바탕으로 한 암호 체계)
-
-
다중 문자 치환 암호 - 서로 다른 문자가 하나의 문자로 치환될 수 있음
-
다중 문자 치환 암호은 각 문자를 다른 문자에 대응시켜서 암호화한다. 하지만, 단일 문자 치환 암호와는 다르게 서로 다른 문자가 같은 문자로 암호화될 수 있다.
-
위의 그림은 다중 문자 치환 암호의 대표적인 예시이다. 평문과 keyword를 토대로, 새로운 문자로 치환을 하는 형식이다. 이를 "비제네르 암호" 라고 한다.
-
이해를 돕기 위해 아래의 사진을 보자.
-
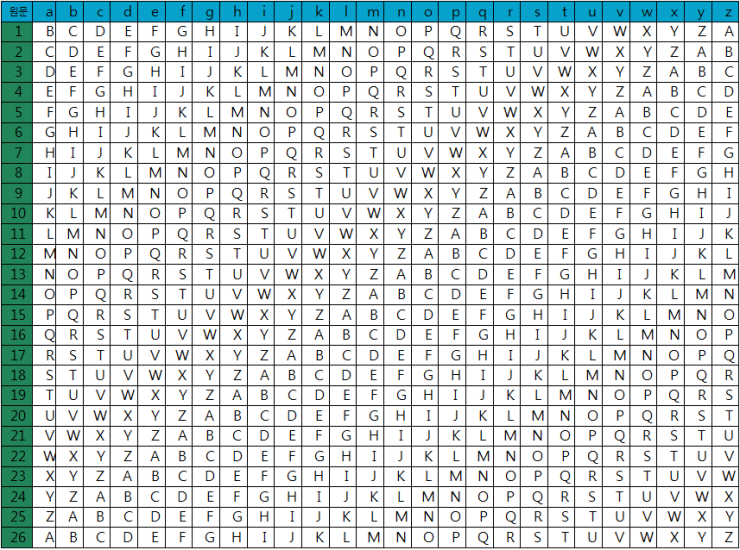
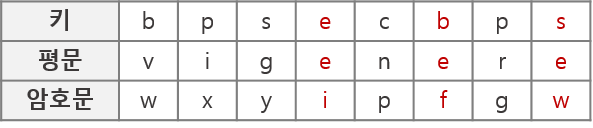
위의 그림은 key와 평문(암호화 전) 을 통해서 암호문을 만드는 표이다. 이 표는 평문 : vigenere, 키 : bpsec 로 하나의 암호문을 만드는 형식이다.
-
처음의 표에서 열의 v,i,g,e,n,e,r,e 를 골라주고, 그에 맞게 키의 알파벳에 맞는 행을 골라주면 그 표에 맞는 것이 암호문이 된다.
-
보다시피 평문이 e 로 같아도, i,f,w 등 여러 문자로 치환될 수 있고, 평문이 v,e 로 달라도 같은 암호문 w가 나올 수 있다.
-
이를 수식으로 표현하게 되면, f(i) = M(i)+K(i) (mod26) 로 표현할 수 있다.
-
>> 전치
전치 암호는 말 그대로 전치 암호이다.
백문이 불여일견. 먼저 어떻게 암호화하는 것인지 살펴보도록 하자.
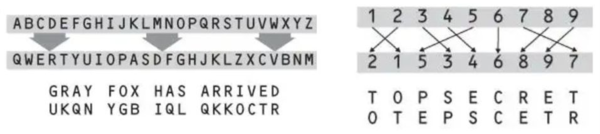
전치는 말 그대로 문자의 위치를 바꾸어주는 암호화 방법이다. 위의 사진을 보면, A~Z 까지의 문자를 순서만 바꿔준 것이 있고, 오른쪽의 'TOPSECRET' 이라는 문자의 순서를 바꾸어 'OTEPSCETR' 로 바꿔주었다. 이처럼 순서를 바꿔주는 암호화 방식을 '전치' 라고 한다.
이 전치의 대표적인 예시로는 '스키테일 암호' 가 있다.

포스팅의 첫 부분에 말했던 원통에 빙빙 감아서 만든 암호이다...! ( 뿌듯..)
이렇게 원통에 감는 방식은 문자를 치환하지 않고, 일련의 규칙에 따라 순서만 바꿔준 것으로, 전치 암호라고 볼 수 있다.
- 고전 암호 공격 -
초반에 고전 암호는 현대에서 쉽게 복호화가 가능하기에 현대에서는 더 이상 쓰이지 않는다고 말했다.
엥..? 그렇다면 치환 암호나 전치 암호를 어떻게 복호화할 수 있을까?
이번에는 고전 암호를 공격하는 방법에 대해서 알아보자.
고전 암호를 공격하는 방식도 2가지로 나눌 수 있다.
- 전수 키 탐색 방법
- 빈도수 분석 방법
이렇게 2가지가 있는데, 차근차근 알아보도록 하자.
>> 전수 키 탐색
전수 키 탐색 방법은 쉽게 말해서 '모든 경우를 탐색' 하는 방법이라고 생각하면 쉽다.
평문 ( 암호화 전 ) 과 암호화 된 암호문을 알고 있을 때, 키가 될 수 있는 모든 경우를 탐색해서 키를 찾아내는 것이 전수 키 탐색 방법이다.
따라서 '카이사르 암호' 같은 경우는 모든 문자가 일정한 거리를 기준으로 밀어서 암호화하는 방식이기 때문에, 26가지만 해보면 정확한 키를 탐색할 수 있게 된다.
하지만, 카이사르 암호 체계가 아니라, 무작위로 알파벳들이 일대일 대응을 이룬다면 어떨까??
계산해보면, 키로 가능한 개수는 26! , 즉 10^26 보다 커지게 된다. 이는 컴퓨터로도 오래 걸릴 수 밖에 없는 키의 범위이다. 따라서 전수 키 탐색은 키의 가능 범위가 좁을 때 유용하게 사용된다.
>> 빈도수 탐색
그렇다면, 위에서 말했던 전수 키 탐색의 단점을 보완해주기 위해 도입한 방법이 '빈도수 탐색' 방법이다. 빈도수 탐색 방법은 쉽게 말해서 '알파벳들의 빈도'로 복호화에 도움을 주는 방법이다.
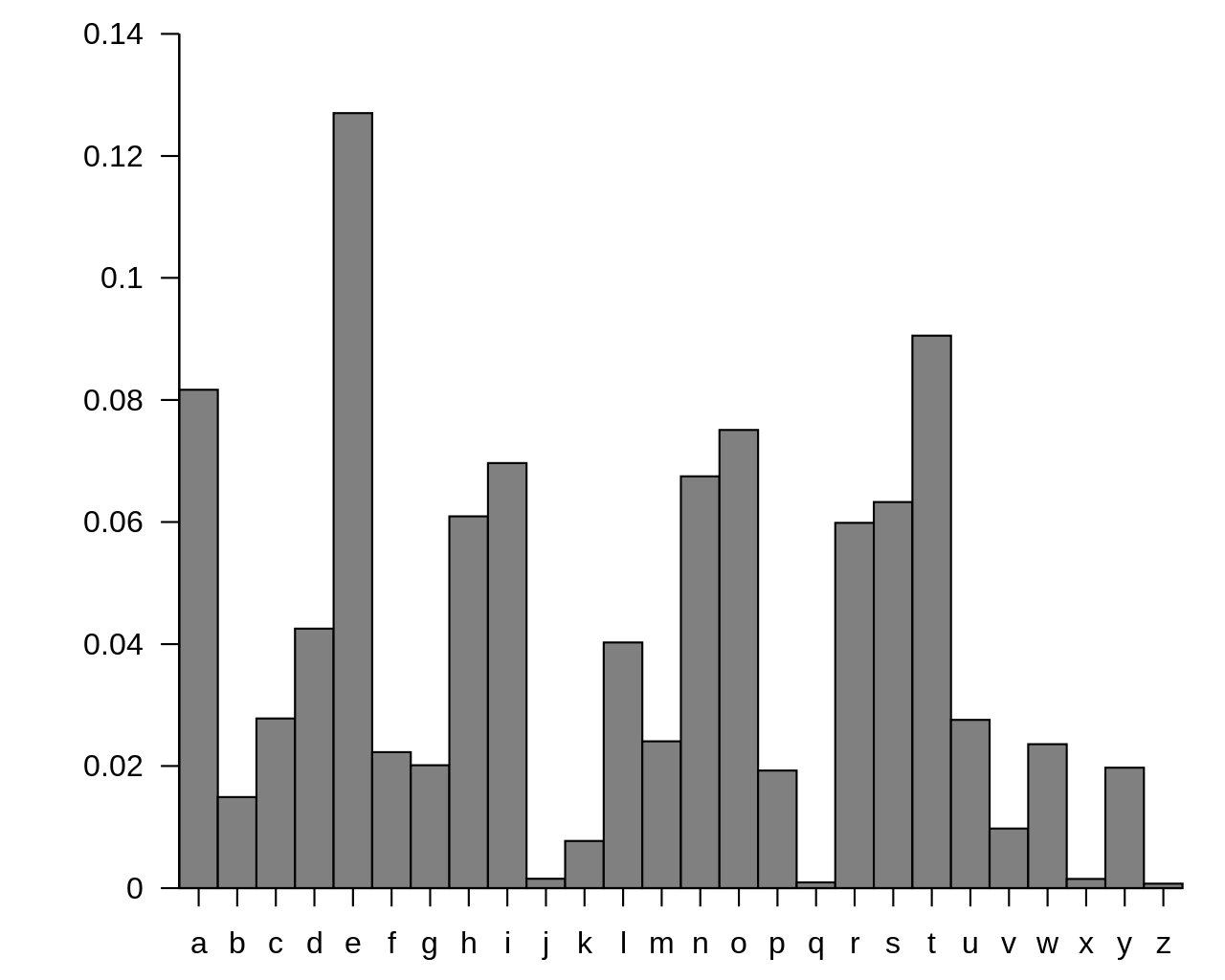
아무리 치환을 무작위로 한다고 해도, 단일 문자 치환은 같은 문자는 같은 문자로 치환되게 된다. 통계적으로, 알파벳을 이용한 문장이 만들어질 때, 위와 같은 통계적 자료가 형성된다. 알파벳중에서 e가 가장 많이 쓰이게 되고, 반대로 j,z,x 가 가장 적게 쓰인다.
이 통계적 특성을 이용해서 치환된 후의 알파벳 중 g 가 가장 많이 쓰였다면, 우리는 e 가 g 로 치환되었다는 예측을 할 수 있게 된다. 따라서 무작위로 대응된 암호 체계라도, 빈도수 탐색을 이요하면 비교적 쉽게 키를 찾아낼 수 있다.
여기까지가 첫번째 Cryptography 이론이다. 다음 포스팅에서는 현대 암호를 설명해보도록 하자 !!