배우면서 쓰는 암호학
내 입으로 말하기는 그렇지만, 솔직히 모든 과목 중 가장 좋아하고, 잘하는 분야를 꼽으라고 한다면 나는 고민없이 수학을 고를 것이다. 정보 보안 분야에 관심을 가지고, 주변 사람들이 암호학에는 행렬과 같은 수학적 지식들을 요구한다고 해서 암호학에 관심을 가지게 되었다. 과연 현대 암호에는 이런 부분들이 존재할지 같이 알아가보도록 하자.
- Key system -
현대 암호에 들어서기 전에, 우리는
- 대칭키 암호 시스템
- 비대칭키 암호 시스템 ( 공개키 암호 시스템 )
이 두 시스템에 관해서 알아야 한다.
과연 이 두 시스템은 무엇이며, 어떤 차이점이 존재할까??
>> 대칭키 암호 시스템
대칭키란 무엇일까??
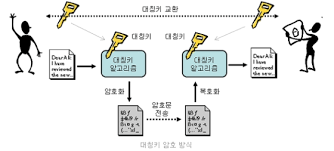
대칭키는 송신자와 수신자가 키를 공유해야 하는 키 시스템을 말한다.
예를 들어, 누군가가 다중 문자 치환 암호 방식을 이용해서 'secret' 문자를 암호화했다고 가정하자.
이 암호화한 문자를 송신자가 수신자에게 보낼 때, 암호화된 문자열만 보내면 수신자가 이를 복호화할 수 있을까??
절대 아니다.
이 암호화에 사용된 키도 동시에 수신자에게 보내야 수신자가 키를 보고 암호화된 문자열을 키를 이용해서 복호화하여 다시 'secret' 라는 문자열을 만들 수 있다.
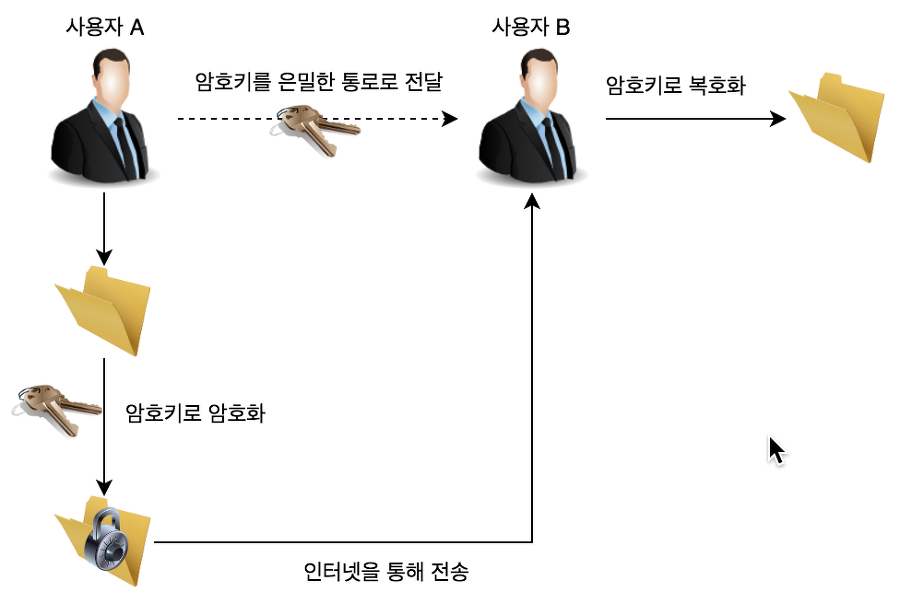
그런데, 이 과정에서 큰 문제점이 하나 있다. 위의 사진에서 나온 "암호키를 은밀한 통로로 전달" 이라는 방식은 어쨌거나 인터넷을 이용한 방식이다. 절대 안전하지 않다. 중간의 불특정 다수가 해킹을 통해서 암호키와 암호화된 문자열을 가로챈다면, 사용자 B(수신자) 와 마찬가지로 복호화까지 할 수 있기 때문에 상당히 위험한 암호 시스템이다.
>> 비대칭키 암호 시스템 ( 공개키 암호 시스템 )
대칭키 암호 시스템을 보완하기 위해서 나타난 방식이 바로 비대칭키 암호 시스템이다.
( 살짝 어렵지만 같이 이해해보자. )

먼저, 대칭키 암호 시스템과 다르게 비대칭키 암호 시스템은
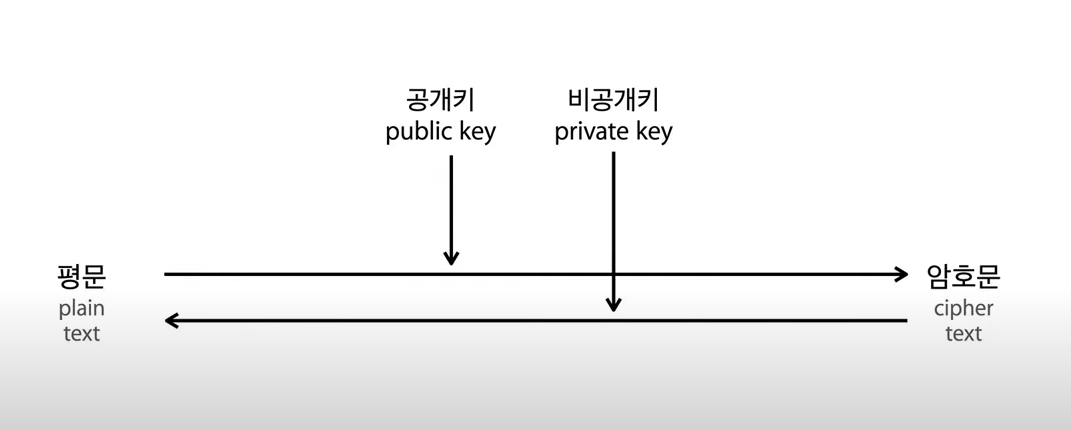
- 공개키 ( Public key )
- 개인키 ( Private key )
이와 같은 총 2개의 키를 만든다.
말 뜻 그대로 수신자가 모든 사람들에게 공개되어도 상관 없는 키인 공개키를 만들고, 절대로 노출되어서는 안될 자신만 가지고 있을 개인키를 만들게 된다.
그럼 비대칭키 암호 시스템의 과정은 다음과 같다.
1. 수신자가 공개키 & 개인키 생성
2. 공개키 공개
3. 수신자의 공개키를 이용해서 송신할 평문을 암호화한다.
4. 송신자가 수신자에게 암호화된 암호문을 전달한다.
5. 수신자는 자신의 개인키를 통해서 암호문을 복호화한다.
아무리 중간에서 해커가 정보를 빼간다고 해도, 해커는 인터넷 상에서 전달된 공개키와 암호문밖에 볼 수 없다. 따라서 수신자만 유일하게 개인키를 가지고 있기 때문에 수신자만 암호문을 복호화할 수 있게 되는 것이다.
여기서 핵심은 공개키로 암호문을 복호화할 수 없다는 것이다!!
음.. 왜 도대체 암호화에 쓰이는 키를 아는데 절대 복호화의 키는 알 수 없다고 하는 것일까??
나는 정보 보안 분야에서 '절대성' 은 없다고 생각하기에 비대칭키 암호 시스템 중 하나인 RSA 암호 체계를 통해 확실히 이해해보도록 하자.
>> RSA 암호
RSA 암호는 오일러 소정리를 이용한 암호 체계이다.
RSA 암호는 (n,e) 라는 공개키를 가지고, d 라는 개인키를 가지게 된다.
여기서 n,e,d 는 어떻게 생성할 수 있을까??
공개키, 개인키 생성 방법
- 임의의 소수 p,q를 지정한다.
- 공개키에 사용될 정수 n = p * q 라고 정의한다.
- 정수 n 의 오일러 파이 함수인 Φ(n) 과 서로소 관계에 있는 임의의 정수 e를 정의한다.
- e * d ≡ 1 (mod Φ(n)) 가 되는 정수 d 를 정의한다. ( 사실 이 부분에서 수학적 기술이 들어가지만, 이번 포스팅에서는 RSA 암호의 체계만 보도록 하자.)
이렇게 4 단계로 공개키와 개인키를 정의할 수 있다.
그럼 이 공개키와 개인키로 어떻게 암호화와 복호화를 진행할 수 있을까??
암호화
- 평문을 M 이라고 하자
- 평문을 암호화한 것이 C 라고 하게 되면
와 같이 나타낼 수 있다.
복호화
- 암호화된 암호문을 C 라고 하자.
- 암호화된 암호문을 d라는 개인키를 토대로
라는 과정을 거치게 되면, 오일러 정리에 의해 복호화할 수 있게 된다.
이렇게 암호화 복호화가 가능하다.
하지만 아직 우리의 의문은 풀리지 않았다.. 도대체 왜 우리는 공개키인 n,e 를 가지고 d를 알아낼 수 없을까??
e * d ≡ 1 (mod Φ(n)) 를 만족하는 d를 찾으면 되지 않을까..?
결론부터 말하자면 d를 찾아낼 수 있다.
그런데 왜 우리는 거의 불가능하다고 하는 것일까?? 여기에는 2가지 이유가 있다.
1. n 을 p * q 꼴로 인수분해하기 매우 어려움.
2. e * d ≡ 1 (mod Φ(n)) 인 d 를 계산하기 매우 어려움.
p 와 q는 매우 큰 소수이기 때문에 소인수분해에 매우 오랜 시간이 소요되기에 인수분해하기 매우 어렵고,
나눗셈의 역연산에도 매우 오랜 시간이 소요된다. 따라서 비대칭키 암호 시스템에서 공개키를 이용해서 개인키를 알아내는 행위는 거의 불가능하다고 볼 수 있다.
자, 그럼 본격적으로 현대 암호에 대해서 알아보도록 하자.
- 현대 암호 -
현대 암호. 무언가 단어만 봐도 어려운 수식들이 많이 써져 있으면서 이상한 문자들이 나열되어 있을 것 같은 기분이다. 과연 현대 암호에는 무엇이 있을까??
현대 암호 시스템은 두가지 성질을 만족해야 한다.
- 혼돈 (Confusion)
- 확산 (Diffusion)
이렇게 2가지 성질이다. 과연 각각은 무슨 성질을 나타내는 용어일까??
>> 혼돈
혼돈은 암호문에서 평문의 특성을 알아내기 힘든 성질을 말한다. 단일 치환 암호를 사용하게 되면,
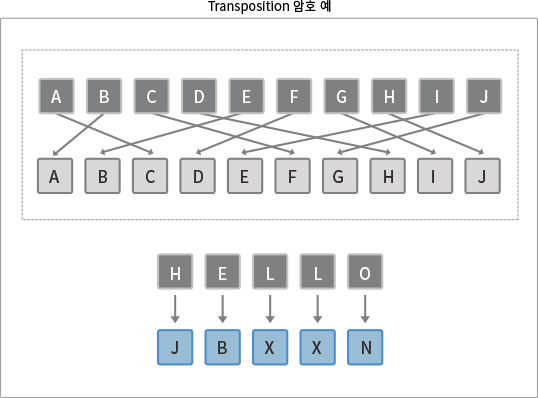
아무리 무작위로 배열한다고 해도, 'HELLO' 라는 문자열은 'JBXXN' 로 치환될 때 같은 문자는 같은 문자로 나타내어지게 된다. 따라서 이는 혼돈의 성질을 만족하지 못한다고 할 수 있다.
>> 확산
확산은 평문의 작은 변화가 암호문의 큰 변화로 이어지는 성질을 말한다. 고전 암호들을 사용하면,
'HELLO' 라는 문자열을 암호화해서 'DFIIS' 가 되었을 때, H 만 바꾸면 암호화된 암호문도 'PFIIS' 처럼 바꾼 평문의 위치만 바뀌게 된다.
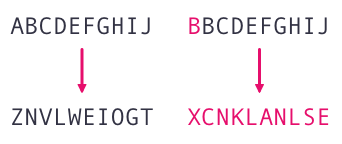
하지만, 확산의 성질은 위의 사진과 같이 'ABCDEFGHIJ' 문자열에서 단순히 A 만 B로 바꾸더라도, 문자열 전체에 큰 영향을 가져와야 한다.
따라서 고전 암호들은 확산의 성질을 만족하지 않는다고 볼 수 있다.
>> Block Cipher - 대칭키 암호
자 그럼 이제 현대 암호에 대해서 알아보도록 하자.
Block Cipher은 '블록 암호'라는 뜻인데, 평문을 정해진 크기의 블록들로 나누어서 각각 암호화한 후에 더하는 암호화 체계이다. 예를 들어서, 단위가 4byte 라고 한다면
- 'fdasjlksdfjlk' → 'fdas' + 'jlks' + 'dfjl' + 'kxxx'
로 나누어서 암호화하게 된다.
예시에서 나왔던 것처럼, 문자열의 길이가 단위의 배수가 아니라 나머지가 남게 된다면, 블록으로 나누기 전에 문자열을 단위의 배수가 되게끔 끝에 데이터들을 붙여주는 작업을 하게 된다. 이를 패딩 (Padding) 이라고 한다.
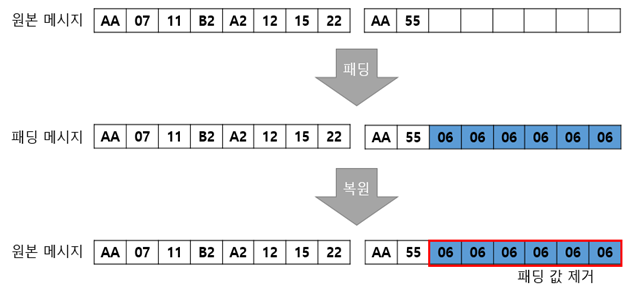
이 패딩된 값들은 나중에 복호화 후에 다시 삭제해주게 된다.
Block Cipher 에는 대표적으로 AES , DES 방식이 있는데, 이는 다음 포스트에서 다루어보도록 하자.
>> Stream Cipher - 대칭키 암호
또 다른 암호로는 Stream Cipher(스트림 암호) 가 있다.
스트림 암호는 송신자와 수신자가 공유하는 데이터 스트림을 생성하고 이를 평문에 XOR하는 암호입니다. 평문을 P, 암호문을 C, 스트림을 X라고 할 때, C = P ⊕ X 로 암호화하게 된다.
복호화할 때는 반대로 C ⊕ X 를 해주면 되는데, C ⊕ X = P ⊕ X ⊕ X = P 이기 때문에 바로 복호화가 가능하다. 하지만 이 방식은 대칭키의 취약점이 너무나도 명확하게 드러나 있다.
따라서 스트림을 모두 공유하는 것이 아니라, 사전에 함수를 합의하고, seed를 공유하여
함수 f(seed) 를 실행함으로써 얻는 스트림을 사용한다.
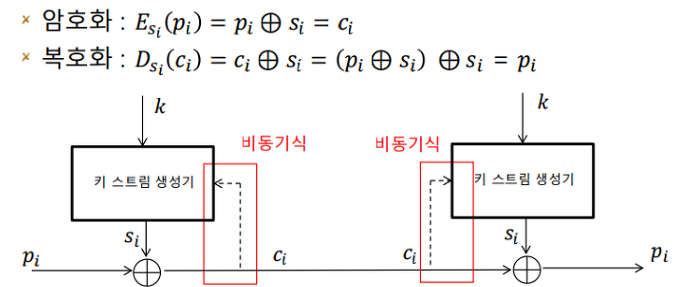
이런 식으로 작동하는데, 여기서 비동기식이라는 말은 동시에 일어나지 않는다는 말이다.
비동기식이 있는 만큼, 동기식도 존재지만, 이번 포스트에서는 Stream Cipher이 무엇인지만 알고 넘어가도록 하자.
여기까지가 현대 암호에서의 기초 중의 기초라고 할 수 있다.
다음 포스트에서는 Block Cipher의 종류인 AES 와 DES 에 대해서 알아보도록 하자.