[논문 리뷰]_Weakly Supervised Object Localization via Transformer with Implicit Spatial Calibration (SCM)

코넬·2023년 9월 9일

PyTorch papers review

PapersReview

목록 보기

24/35

Weakly Supervised Object Localization via Transformer with Implicit Spatial Calibration

Introduction

본 논문은 이미지 레벨 라벨만 사용하여 객체를 정확하게 localize하는 새로운 방법을 제안합니다.

Introduction에서 Weakly Supervised Object Localization(WSOL)의 중요성과 WSOL에서의 challenge를 설명합니다. WSOL은 객체 검출과 같은 강력한 지도학습을 사용하지 않고도 객체를 localize할 수 있는 중요한 분야입니다. 그러나 WSOL은 객체의 정확한 경계를 찾는 것이 어렵기 때문에, 이를 개선하기 위한 다양한 시도가 있었다고 설명합니다.

이 논문에서는 Semantic Coherence와 Spatial Connectivity를 결합하여 정보를 전파하는 방법을 개선하고, 객체를 정확하게 localize하는 Spatial Calibration Module (SCM) 을 제안합니다.

SCM은 Transformer Encoder와 Decoder를 사용하여 이미지의 Semantic Coherence와 Spatial Connectivity를 모델링하고, 이를 통해 객체의 정확한 경계를 찾을 수 있습니다.

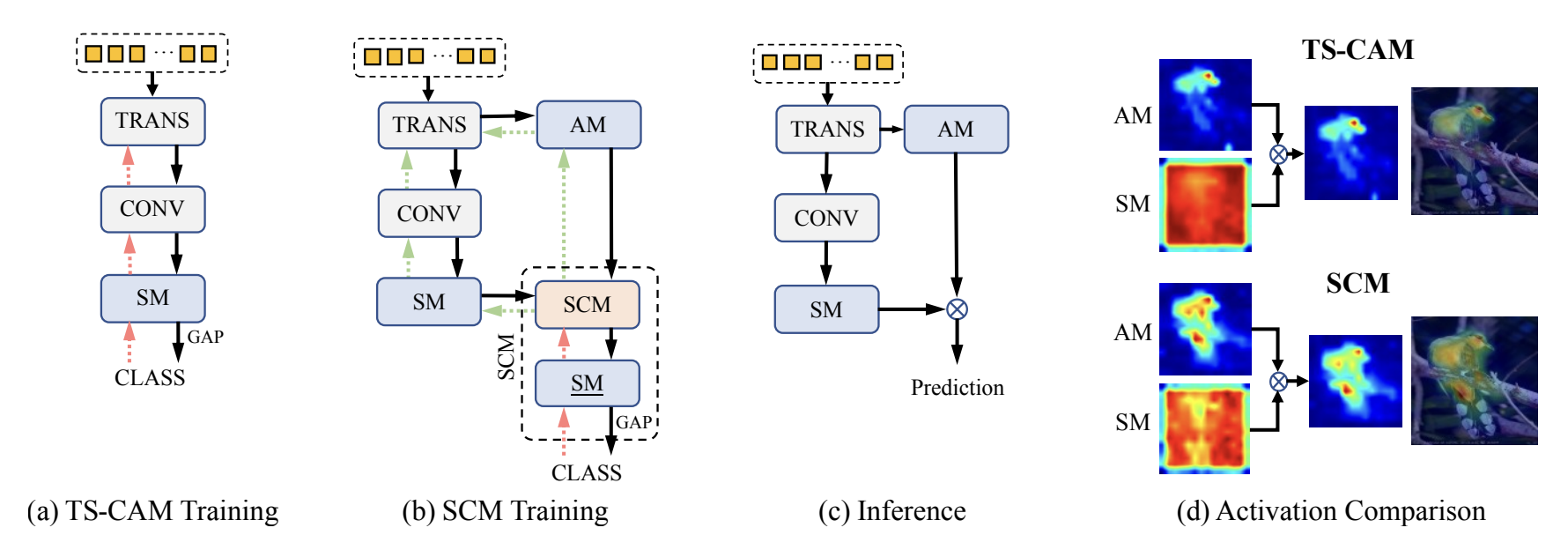
(a) 는 SCM 과 비교하기 위한 TS-CAM의 구조를 보여줍니다. TS-CAM은 Class Activation Map (CAM)을 기반으로 하며, 입력 이미지에서 Semantic Coherence를 모델링합니다. 이를 위해, Global Average Pooling (GAP)을 사용하게되는데, GAP은 입력 이미지의 feature map에서 각 채널의 평균값을 계산하여, 클래스별 활성화 맵을 생성합니다. 이렇게 생성된 활성화 맵은 객체의 위치를 찾는 데 사용됩니다.

그러나 TS-CAM은 객체의 정확한 경계를 찾는 데 어려움이 있습니다. 이는 Semantic Coherence만을 고려하기 때문입니다.

Semantic Coherence 란?
Semantic Coherence는 입력 이미지에서 객체의 의미적 일관성을 모델링하는 것을 의미합니다. 즉, 입력 이미지에서 객체와 관련된 특징들이 서로 유사하게 분포되어 있을 때, Semantic Coherence가 높다 고 할 수 있습니다.

예를 들어, 고양이 이미지에서 고양이의 귀, 코, 눈 등의 특징들은 서로 유사하게 분포되어 있는데, 이러한 특징들이 Semantic Coherence를 나타내고, 객체의 정확한 경계를 찾는 데 중요한 역할을 합니다.

이 논문에서는 Semantic Coherence를 모델링하기 위해 Transformer Encoder를 사용합니다. Transformer Encoder는 입력 이미지에서 Semantic Coherence를 모델링하여, 객체의 특징을 추출합니다. 이를 통해, 객체의 위치를 찾는 데 사용됩니다.

따라서 본 논문에서는 SCM 을 제안하게 되는데, SCM 은 Semantic Coherence와 Spatial Connectivity를 모두 고려하여, 객체의 정확한 경계를 찾을 수 있다고 합니다.

(b) 는 Transformer Decoder의 입력으로 사용되는 Semantic Map 을 확인할 수 있습니다. Semantic Map은 입력 이미지에서 추출된 객체의 의미적 정보(semantic representations)를 나타내는 map을 추출할 수 있습니다.

(c)는 WSOL에서 추론을 진행하는 부분으로, Transformer Decoder의 출력으로 사용되는 Attention Map과 SCM Training 에서 output 으로 나온 SM 을 합쳐 final localization prediction을 위한 최종 Map 을 출력합니다.

(d)애서는 AM, SM, and final activation maps of TS-CAM and proposed SCM을 비교하여 보았는데요, SCM 이 기존의 TS-CAM 보다 객체의 localization을 훨씬 더 잘 하는 모습을 볼 수 있습니다.

이와 같이 SCM 모델을 도입했을 시, 실험 결과가 WSOL 분야에서 새로운 접근 방식을 제안하고, 다양한 실험을 통해 다른 최신 기술들과 비교하여 우수한 성능을 나타냄을 보여주고 있습니다.

Spatial Calibration Module

SCM 이 나온 배경에 대해서도 이야기합니다. 기존의 Vision Transformer 이 해결한 long-range global dependency 와, global structure을 뽑아내기 위한 TS-CAM의 등장, 그러나 여기서 발생하는 정확한 경계를 찾는 것에 대한 어려움 (그림 d 를 확인해보면, TS-CAM에서는 작은 밀집된 구역의 경계(새의 윗몸통부분)만 capture 하는 모습을 확인할 수 있습니다. ) 에 대해 이야기하며,

새의 털(아래 끝부분)은 주변 영역에 엄청난 변화를 일으키지 않고, 그것의 의미론적 맥락은 활성화된 영역에서 전파되어 전체 body를 덮을 수 있도록 하는 정확한 결과를 제공할 수 있다는 것 또한 저자들이 확인했다고 합니다.

이 잠재적 연속성(potential continuity) 에 영감을 받아, 새로운 외부 모듈인 Spatial Calibration Module(SCM) 을 만들게 되었고, 더욱 뚜렷한 경계를 나타낸 activation map 을 transformer 를 통해 만드는 module 입니다.

SCM는 Transformer의 주의 표현을 암시적(implicitly)으로 보정하고, 공간 및 문맥적 일관성에 기반하여 기능적인 영역을 더욱 의미 있는 활성화 맵으로 생성합니다. 본 논문의 핵심 디자인인 unified diffusion model 은 패치 토큰의 의미적 유사성과 지역 공간 관계를 훈련 중에 포함시킵니다. 추론(inference) 단계에서는 SCM을 삭제하여 모델의 단순성을 유지하며, 그림 1(c)와 같이 보정된 Transformer 백본을 사용하여 Semantic Map (SM)과 Attention Map (AM)을 결합하여 위치 파악 결과를 예측한다는 것이 큰 틀입니다.

main contribution은 다음과 같이 정리할 수 있습니다.

저자들은 새로운 외부 트랜스포머 모듈을 SCM 으로 제안하였고, 이는 WSOL 모델들 중 부분적으로 활성화되는 문제를 공간적인 관계를 영향을 주도록 만들어 해결할 수 있도록 하였습니다. 특히, SCM 은 트랜스포머를 암시적으로 최적화하기 위해 추론 하는 도중에 빠지도록 만들었다고합니다.
저자들은 유연한 방식을 제공함으로써 새로운 정보 이동 방법을 제안하였습니다. 이 유연한 방식은 공간적으로, 의미적인 관계를 통합시켜 의미적으로 풍부한 영역을 확장시키고, 완벽하게 객체를 포함할 수 있도록 한 방식입니다. 예를 들어, 저자들은 학습가능한 파라미터를 도입하였다고 하는데요, 이는 diffusion 범위를 조절하고, 노이즈를 필터링할 수 있도록 만들어 유연하게 컨트롤가능하고 어떠한 입력 이미지에서도 잘 작동할 수 있도록 만들어준다고 합니다.
넓은 범위의 실험은 제안된 프레임워크가 WSOL 벤치마크를 상대할 수 있도록 뛰어난 성과를 입증합니다.

Weakly Supervised Object Localization

' The weakly supervised object localization aims to localize objects by solely image-level labels. '

이것이 WSOL의 핵심입니다. 이미지 레벨의 라벨만 가지고 object localization을 진행하는 것입니다. WSOL 의 가장 큰 문제점은 limited discriminative regions 인데요, 이는 객체 전체를 다 포함시킬 수 없다는 문제점이죠.

이 문제들을 해결하기 위해 다양한 WSOL 모델을이 어떤 방식으로 이를 개선하려 했는지를 주르륵 말해줍니다. (참고로 이 모델들은 전부 CNN backbone의 모델입니다.)

따라서 저자는 CNN backbone 모델 대신 Transformer backbone 의 모델을 사용하기로 하였으며, 기존의 transformer block 에 모듈을 끼워넣는 것은 굉장히 성가신 일이기 때문에 external module 을 사용하였다고 합니다.

Graph diffusion

그래프 확산(Graph Diffusion) 은 그래프 구조에서 정보 흐름의 과정을 의미합니다. 본래 이미지에서는 픽셀들이 강한 상관관계를 보이며, 이러한 관계를 포착하기 위해 그래프 구조를 구성하는 것이 많은 관심을 받고 있습니다. 그래프 확산 알고리즘인 Graph Diffusion Kernel (GDK) 알고리즘은 부분 활성화 결과를 기반으로 완전한 의사 마스크(pseudo mask)를 추론하는 데 사용될 수 있습니다.
GDK는 초기에는 사회망, 검색 엔진 및 생물학에서 유전자 상호작용 네트워크의 경로 멤버십을 추론하는 데 사용되었습니다. 논문에서는 WSOL에서 부분 활성화 결과를 기반으로 완전한 의사 마스크를 추론하기 위해 전통적인 GDK 알고리즘을 수정하였다고합니다. 그래프 구조는 많은 클래식 그래프 알고리즘을 가능하게 하며, 이미지 속성에 대한 새로운 통찰력과 이해를 제공하기에 사용하였습니다. (의미론적 내용을 담을려 하다보니 사용한 것같습니다.)

Methodology

전반적인 구조

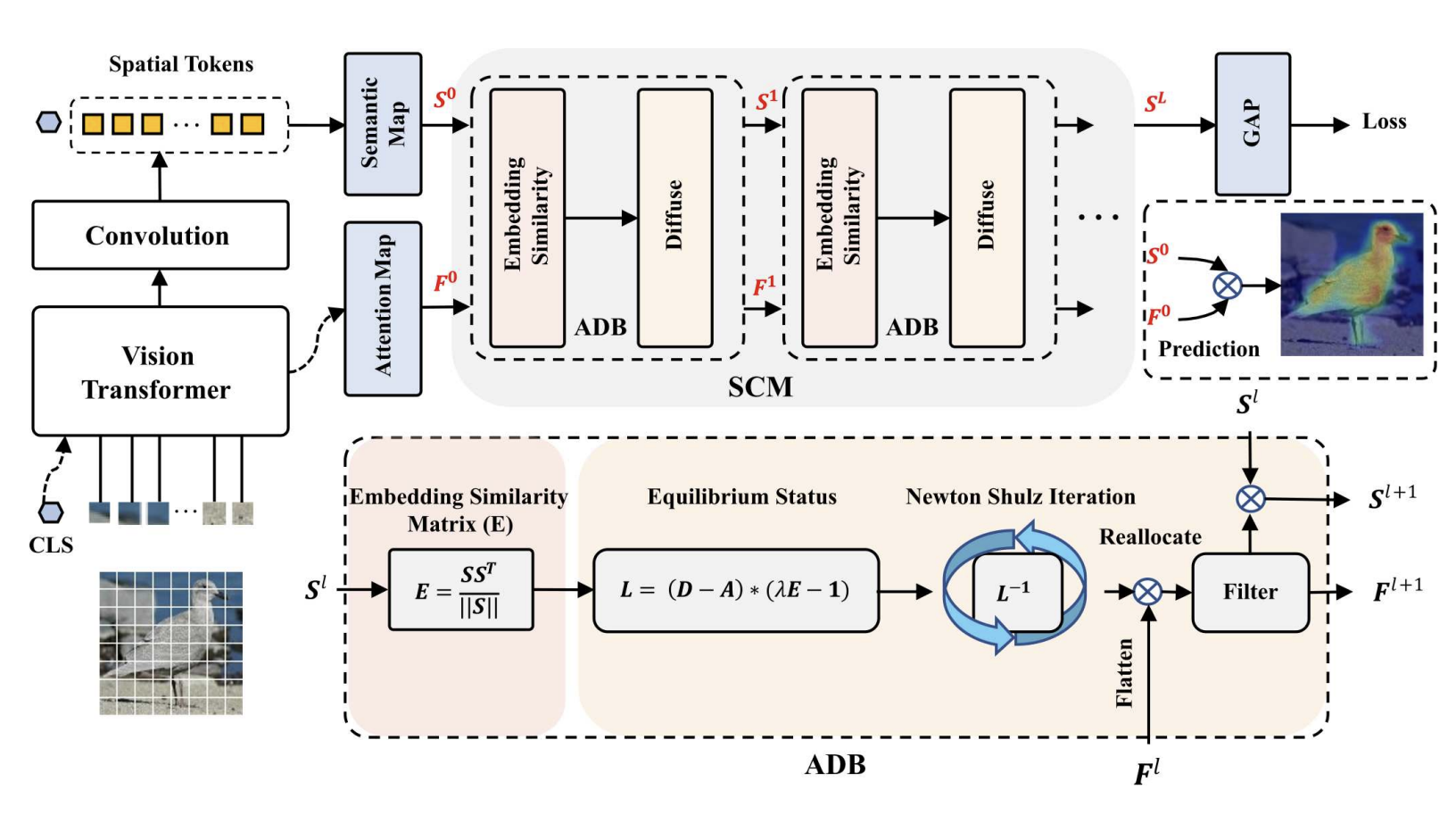
위의 이미지는 SCM이 사용된 WSOL transformer 모델의 전반적인 framework 를 담고 있습니다.

가장 큰 부분은 두가지, Spatial Calibration Module ( SCM ) 과 이를 만들기 위해 쌓여진 다량의 activation diffusion blocks ( ADB ) 에 대해 이해하면 됩니다.

ADB 는 몇개의 서브모듈로 이루어져있는데요, 의미론적 유사도 측정과, 활성화 diffusion, diffuse 행렬 추정, 그리고 다이나믹 필터링으로 구성되어있습니다.

Spatial Calibration Module

SCM 은 특정한 부분만 activation 하는 문제를 완화하기 위하여 작은 영역에서 바깥 영역으로 activation을 분산시켜놓았다고 할 수 있습니다.

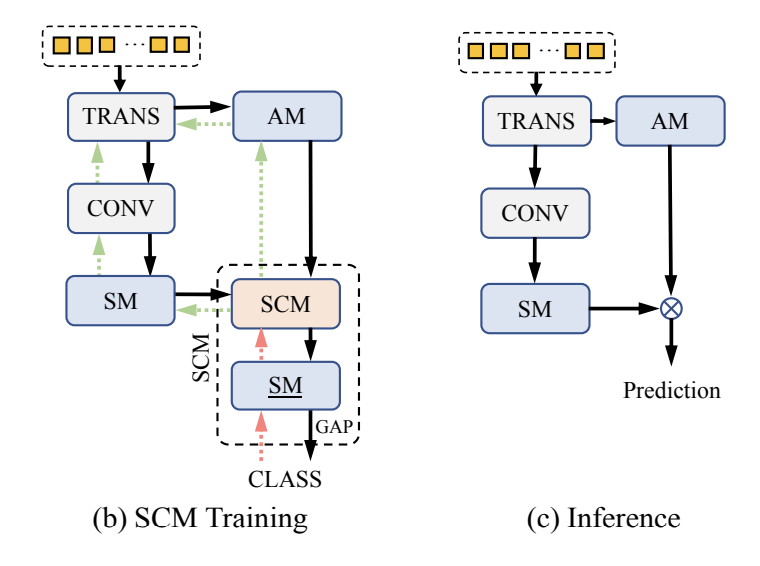
넓은 관점에서, (b)를 다시보면 트랜스포머는 attention map(AM) 과 semantic map(SM) 을 보며 조정을 진행하고 (SCM 에서 semantic loss를 사용하며),

Input 이미지는 $N = H * W$ 패치로 나눠지고 각각은 토큰으로 불리며, $(H,W)$ 는 패치의 해상도를 말합니다.

패치 토큰과 CLS 토큰으로 나눠진 후, I로써 트랜스포머 블록으로 들어가게 되며, 이는 추가적인 표현학습을 하는데 사용됩니다.
TS-CAM 과 비슷하게, 초기 attention map 을 $F^0 \in R^{H*W}$ 로 세우고, self-attention matrix를 $W_i \in R^{(N+1)*(N+1)}$ 로 $i$ 번째 층에 세운 후, 평균을 내어 multiple self-attention heads 를 만듭니다.

여기서 $M_i \in R^{H*W}$ 를 attention 가중치로 두었으며, 트랜스포머의 $F^0$ 을 구하기 위하여 (클래스 토큰과 일치) 모든 중간 층들을 $(M_i)^I_{i=1}$ 로 평균내었습니다.

F^0 = \frac{1}{I} \sum^I_{i=1}M_i

자, 이제 다음으로 semantic map $S^0 \in R^{H*W*C}$ 을 얻기 위해, (여기서 C는 카테고리 갯수) 모든 공간적 토큰인 $(t_n)^N_{n=1}$ 을 마지막 트랜스포머 레이어층에서 뽑아내고, 그들을 conv head 인

S^0 = reshape(t_1...t_N)*k

로 변형시켜줍니다. k 가 3 * 3 의 conv kernel 이고, reshape 를 통해서 2차원 맵의 토큰 시퀀스로 바꿔주는 작업을 진행합니다.

그리고 나서 마지막으로 이렇게 구한 $F^0$ 과 $S^0$ 을 SCM 으로 보내주면 과정이 완료됩니다.

Activation Diffusion Block

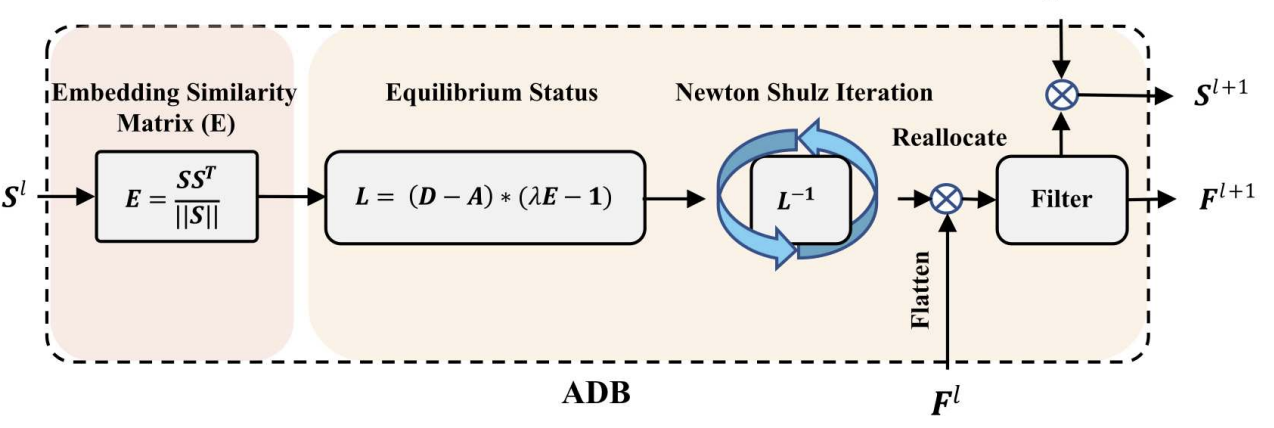
ADB 처리 과정부터 살펴보겠습니다.

Embedding Similarity Matrix

$S^l$ 이 input 으로 들어오게 되면, $S^l$ 의 패치 쌍 간 임베딩 유사성( $E$ )을 추정합니다.

E^l_{i,j} = \frac{v^l_i(v^l_j)^T}{||v^l_i||||v^l_j||}

여기서 $E^l_{i,j}$ 는 코사인 거리 계산으로 정의되고, $v^l_i$ 와 $v^l_j$ ( 이 둘은 평탄화된 벡터 ) 간의 얼마나 유사성이 높은지를 나타내는 수치가 됩니다.

Equilibrium Status

그런 다음 E를 사용하여 $L^l$ 의 역수가 나타내는 평형 상태로 $F^l$ 을 확산하여 활성화 상태를 확장시킵니다. 실제로, 논문에서는 Newton Shulz 반복법 을 사용하여 $(L^l)^{-1}$ 을 근사적으로 다시 활성화 작업을 진행합니다.

L을 계산하는 식을 보면, 라플라시안 행렬을 L 로 표현하였습니다.
그래프 표현에 대한 최근 연구에서 라플라시안 행렬의 역수가 전역 확산(global diffusion) 을 이끌어내어 각 유닛들이 서로 communicate 할 수 있게 한다는 것을 보여줍니다.
따라서 노드 context 정보 $E^l$ 과 함께 $\hat{L^l}$ 을 활용하여 의미론적 관계를 강화하여 확산을 향상시킵니다. 직관적으로, 저자는 공간적 연결성과 의미론적 일관성을 활용하여 토큰을 의미론적으로 우선시되는 전경 객체와 배경 환경으로 분할합니다.

실제로, 저자는 의미론적 강도를 유동적으로 조정하는 학습 가능한 매개 변수 λ를 사용하여 확산 과정을 더 유연하고 다양한 상황에 적합하게 만듭니다.

의미론적 정보를 포함한 라플라시안 행렬 $L^l$ 은 다음과 같이 정의됩니다.

L^l = (D^l - A^l) ⊙ (λE^l - 1)

⊙ 기호는 요소별 곱을 나타내며, 1은 이웃하는 정점 간의 정보 흐름 교환을 나타냅니다. $(D^l - A^l)$ 은 공간적 연결성을 나타내며, $(λE^l - 1)$ 은 의미론적 일관성을 나타냅니다. ⊙ 를 통해 이러한 요소들을 확산에 통합합니다.

전달된 출력 재할당된 attention map은 $F^l+1$ 로 표시되고, Γ는 $F^l$ 을 패치 시퀀스로 재구성하는 평탄화 작업을 나타냅니다. global diffusion 후의 재할당된 activation score 맵을 계산하는 방정식은 다음과 같습니다.

F^{(l+1)} = (L^l)^{-1}Γ(F^l)

Newton Shulz Iteration

그 후, 동적 필터링 모듈(dynamic filtering module) 이 적용되어 과도하게 확산된 부분을 제거합니다.

$L^l$ 를 통해 역행렬한 $(L^l)^{-1}$ 을 바로 사용하게 되면, 일단 $L^l$ 이 무조건 양수라는 보장도 없으며, 역행렬을 취했을 때 존재하지 않는 수 일 경우도 있기 때문에, 이러한 문제를 해결하기위해 Newton Shulz Iteration 를 사용하여 $(L^l)^{-1}$ 를 global diffusion 할 수 있도록 근사를 진행합니다.

X_0 = \alpha(L^l)^T \\ X_{p+1} = X_p(2I - L^lX_p)

여기서 $X_0$ 는 초기값이며, p 는 반복된 횟수를 나타내고, I 는 단위행렬을 나타냅니다. p 번 시행이 반복 될수록 global diffusion 한 값으로 근사가되는 모습을 확인할 수 있다고합니다.

Reallocate

마지막으로, 개선된 $F^l$ 은 요소별 곱셈을 통해 $S^l$ 을 업데이트합니다. 여러 개의 ADB를 쌓음으로써, 두 맵의 강도가 의미와 공간적 특징을 균형있게 조정됩니다. 이 때, 나타나는 문제점이 불필요한 뒷 배경도 중첩되어 쌓이게 되어, 바깥 노이즈를 억누르는 과정을 진행하는데요,

\tau(F^l,\beta) = \beta \cdot tanhShrink(\frac{F^l}{\beta})

$\beta$ 는 더 유연한 조정을 위해 문턱 파라미터이며, $\tau$ 는 부드러운 문턱 함수, tanhShrink 같은 경우에는 $tanhShrink(x) = x - tanh(x)$ 로 뒷배경 활성화를 억누르는 역할을 합니다.

$S^{l+1} = S^l ⊙ \tau(F^l,\beta)$ 이 과정을 통해 노이즈를 없애고 대조되는 부분은 더욱 두드러지게 만드는 과정을 진행합니다.

Prediction

위의 과정을 거쳐서 경계가 뚜렷한 WSOL 과정이 진행되는데요, 이러한 방식을 통해 트랜스포머가 object-boundary aware activation maps 을 생성하게됩니다.

위에서 언급하였듯, 과정을 단순화하기 위하여 이제는 SCM을 drop 하고 prediction을 진행합니다.

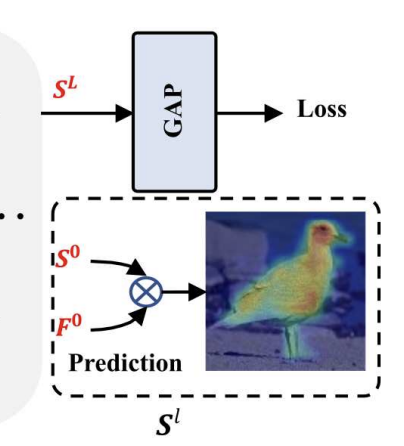
bounding box 예측은 $S^0$ 와 $F^0$ 을 결합하여 진행하는데요, S는 C 채널의 2차원 의미론적 맵이고, 각 채널은 특정 클래스 c 에 대한 표현을 담은 활성화 맵입니다.

예측에 대한 score map 을 얻기 위하여,
1. $S^0$ 를 GAP 으로 통화시켜 classification 스코어를 계산합니다.
2. 가장 classification 스코어가 높은 i 번째 S map 을 선택합니다.
3. $F^0 ⊙ S^0_i$ 를 element-wise product 를 진행하여 계산합니다.

이 통합된 결과는 bounding box 예측의 input 값과 동일한 사이즈로 만들어집니다.

Results

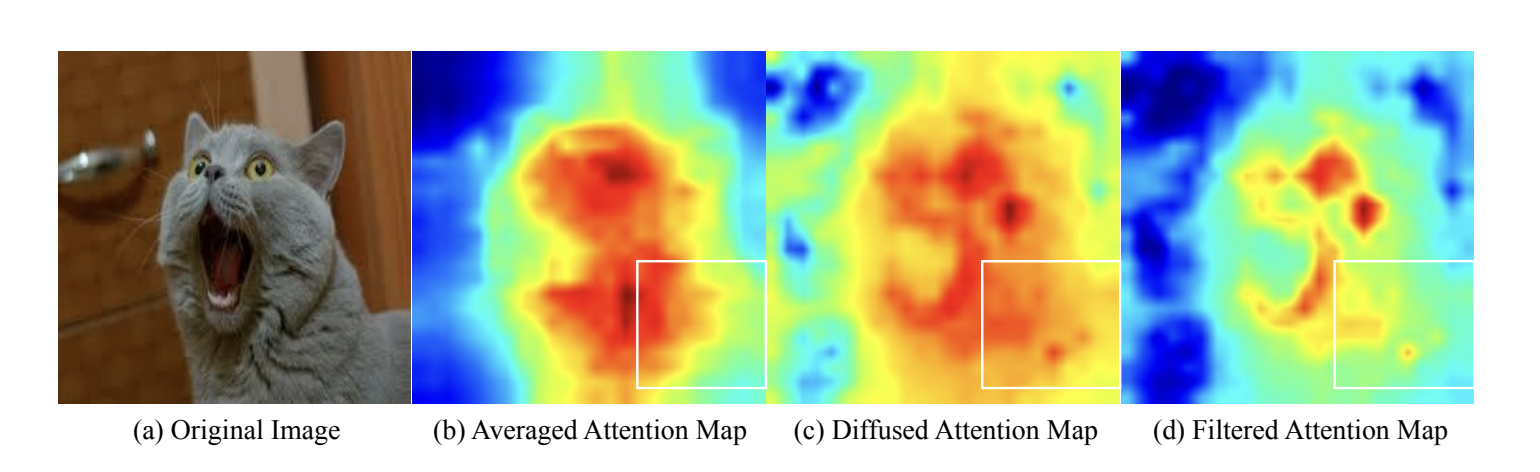
모델의 activation map 을 확인해보면, 기존의 트랜스포머의 activation map 과 c를 거쳐 필터링된 d의 activation map을 비교해보면, 공간적 응집성이 d 에서 더 강하게 나타나는 것을 확인할 수 있고, 이를 활용하게된다면 객체의 경계를 더욱 뚜렷하게 잡을 수 있다고 합니다.

SCM을 활용한 결과를 확인해보면,

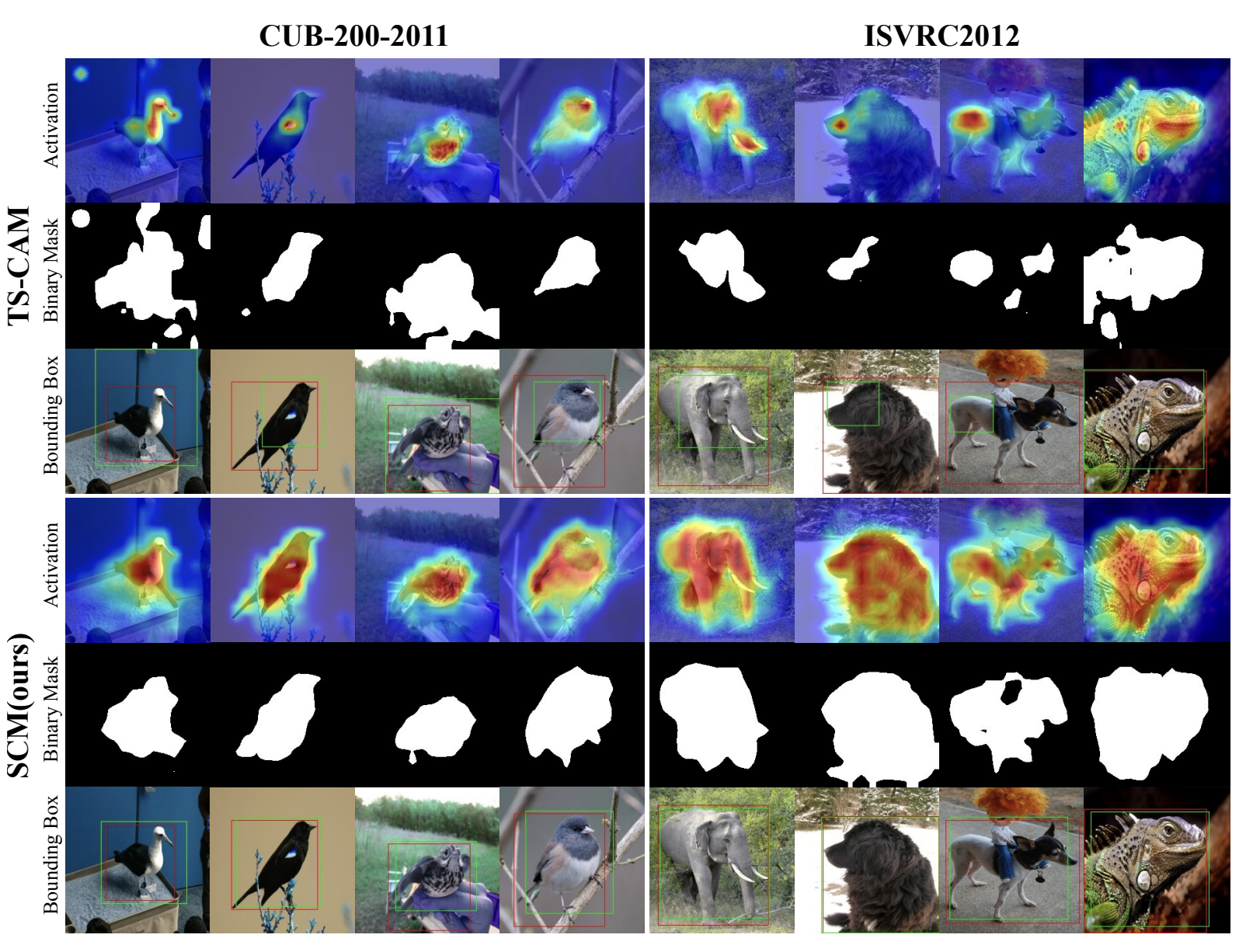
기존의 TS-CAM 보다 훨씬 더 객체의 전반적인 영역을 따냈으며, 노이즈 없이 특정 부분만 보는 WSOL 의 문제점까지도 해결된 모습을 확인할 수 있습니다.

수치적으로 결과를 확인해보면, (~~개인적으로 저는 크게 향상된건지는 잘 모르겠지만~~) Top-5 loc 가 다른 기법들에 비해서 향상된 모습을 확인할 수 있습니다.

Weakly Supervised Object Localization via
Transformer with Implicit Spatial Calibration - 논문 보기

코넬

어서오세요.

이전 포스트

[논문 리뷰]_Pixel Recurrent Neural Network

다음 포스트

[논문 리뷰]_Weakly Supervised Object Localization via Transformer with Implicit Spatial Calibration (SCM)

PapersReview

Weakly Supervised Object Localization via Transformer with Implicit Spatial Calibration

Introduction