[논문 리뷰]_GAN : Generative Adversarial Nets

코넬·2023년 9월 11일

PyTorch papers review

PapersReview

목록 보기

25/35

Generative Adversarial Nets

generative model 의 시초라 볼 수 있는 Generative Adversarial Nets 는, 중요한 모델이기 때문에 papers 의 순서대로 정리해보았습니다.

Abstract

본 논문에서는 새로운 프레임워크인 '경쟁하는(adversarial) 과정' 을 통해서 생성 모델을 추정하는 방법을 제안하였습니다.

이는 동시에 2개의 모델을 훈련시키는데요,

첫번째는 생성모델(generative model) G 로, training data 의 분포를 capture(묘사) 하여 discriminative model 이 구분하지 못하도록 합니다.
두번째는 판별모델(discriminative model) D 로, 샘플 데이터가 생성 모델로부터 나온 데이터가 아니라, 실제 training data 에서 나온 데이터일 확률을 추정합니다.

여기서 G를 학습하는 과정은 D 가 샘플 데이터가 G로부터 나온 가짜 데이터와 실제 training data 를 판별하는데 오류를 범할 확률을 최대화하는 과정이라고 볼 수 있습니다. (생성된게 진짜라고 판별되어야 좋은 모델이니까요)

본 논문에서는 이러한 framework를 minimax two-player game 으로 표현하고 있습니다. (자세한 내용은 뒷부분에)

임의의 함수(모델은 함수로 이루어짐) G, D의 공간에서 G가 training data 분포를 모사(cover)하기 때문에, D가 실제 training data인지 G가 생성해낸 가짜 데이터인지 판별할 수 있는 확률은 1/2가 됩니다. (즉, 실제 데이터와 G가 생성해내는 데이터 간의 판별이 어려워진다는 뜻이죠)

G와 D가 multi-layer perceptrons 으로 정의된 경우, 전체 시스템은 back-propagation을 통해 학습됩니다.

Introduction

GAN 이 나오기 전에, 딥러닝이 작동하는 방식은 input 데이터의 종류에 대해서 모집단에 근사하는 확률 분포를 나타내는 계층모델을 발견하는 것이였습니다.
따라서 고차원의 방대한 정제된 데이터를 클래스 레이블에 1:1로 mapping하여 구분하는 모델 사용하였습니다. (well-behaved gradient를 갖는 선형 활성화 함수들을 사용한 backpropagation, dropout 알고리즘 기반)

도입부에서 기존 생성 모델에 대해 문제점을 이야기하고있습니다.
Deep 생성모델(generative model)들은 maximum likelihood estimation과 관련된 전략들에서 발생하는 많은 확률 연산들을 근사하는 데 발생하는 어려움과 generative context에서는, 앞서 모델 사용의 큰 성공을 이끌었던 선형 활성화 함수들의 이점들을 가져쓰는 것에 어려움이 있었기 때문에 크게 좋은 성능을 이끌지 못하였습니다.

본 논문의 생성 모델은 이러한 문제점을 해결 X 회피하여 모델을 짜는데, 이 생성 모델은 adversarial nets 로, (프레임워크 : ‘경쟁’) discriminative model은 sample data가 G model이 생성해낸 sample data인지, 실제 training data distribution인지 판별하는 것을 학습합니다.

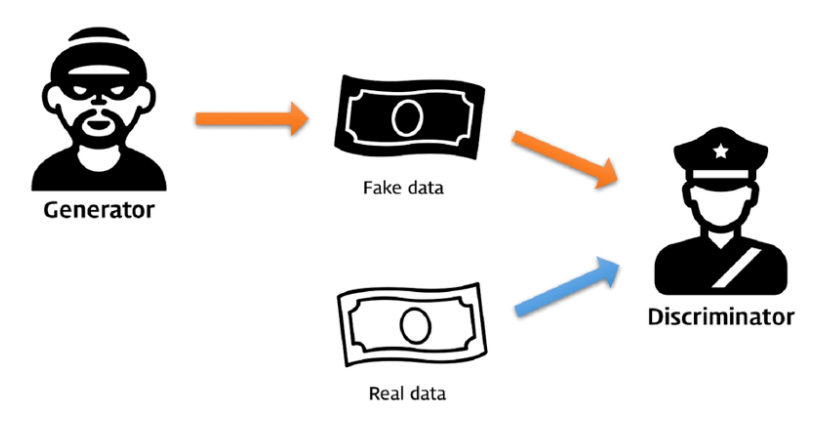
너무나도 유명한 예시인데요, 이것만큼 잘 설명하는 그림은 없을 것같아 가져왔습니다.
GAN의 경쟁 과정을 경찰(분류 모델, 판별자, discriminative model) 과 위조지폐범(생성 모델, 생성자, generative model) 사이의 경쟁으로 비유해봅시다.

위조지폐범은 최대한 진짜 같은 화폐를 만들어 경찰을 속이기 위해 노력하고, 경찰은 진짜 화폐와 가짜 화폐를 완벽히 구분하여 위조지폐범을 검거를 목표로 합니다. 이러한 과정을 반복하다보면 어느 순간 위조지폐범이 진짜와 다를 바 없는 위조지폐를 만들 수 있고 경찰이 위조지폐를 구별할 수 있는 확률 또한 50%로 수렴하게 됨으로써 경찰이 위조지폐와 실제 화폐를 구분할 수 없는 상태에 도달하게됩니다.

GAN의 목적은 각각의 역할을 가진 두 모델을 통해 적대적 학습을 하면서 ‘진짜같은 가짜’를 생성해내는 능력을 키워주는 것이라고 할 수 있습니다.

본 프레임워크는 많은 특별한 학습 알고리즘들과 optimization 알고리즘을 사용할 수 있으며, 위에서 설명하듯 multi-layer perceptron을 사용하면 다른 복잡한 네트워크 필요 없이 오직 forward propagation/ back propagation / dropout algorithm으로 학습이 가능합니다.

Adversarial Net

Adversarial model 프레임워크 는 앞서 말했듯이 가장 간단하므로, multi-layer perceptrons 모델에 적용합니다.

학습 초반에는 G(generative model) 가 생성해내는 이미지는 D(discriminative model) 가 G가 생성해낸 가짜 샘플인지 실제 데이터의 샘플인지 바로 구별할 수 없기 때문에, D(G(z))의 결과가 0에 가깝습니다.

D(G(z)) : z로 부터 G가 생성해낸 이미지가 D가 판별하였을 때 바로 가짜라고 판별할 수 있다고 하는 것을 수식으로 표현한 것

그리고 학습이 진행될수록, G는 실제 데이터의 분포를 모사하면서 D(G(z))의 값이 1이 되도록 발전하게됩니다. 이는 G가 생성해낸 이미지가 D가 판별하였을 때 진짜라고 판별해버리는 것을 표현한 것이 됩니다.

\underset{G}min \underset{D}maxV(D,G) = \mathbb{E}_{x\sim{p_{data}(x)}}[logD(x)] + \mathbb{E}_{z\sim{p_z(z)}}[log(1-D(G(z)))]

위의 수식을 확인해보면,

첫번째 항은 real data x 를 discriminator 에 넣었을 때 나오는 결과를 log취했을 때 얻는 기댓값이라고 볼 수 있으며,
두번째 항은 fake data z 를 generator에 넣었을 때 나오는 결과를 discriminator에 넣었을 때 그 결과를 log(1-결과)했을 때 얻는 기댓값이라고 볼 수 있습니다.
마지막으로 G 입장에서는 loss가 최소가 되어야 자기가 만든 가짜 데이터가 진짜라고 판별될 수 있기에 min 이며,
D 입장에서는 loss 가 최대가 되어야 가짜 데이터를 가짜라고 판별할 수 있게 되기 때문에 max 라고 작성하게됩니다.

더 자세히 이해해보기
이 방정식을 D의 입장, G의 입장에서 각각 이해해보면, 먼저 D의 입장에서 이 value function V(D,G) 의 이상적인 결과를 생각해보면, D가 뛰어나게 판별을 잘 해낸다고 했을 때, D가 판별하려는 데이터가 실제 데이터에서 온 경우에는 D(x)가 1이 되어 첫번째 항은 0이 되어 사라지고 G(z)가 생성해낸 가짜 데이터를 구별해낼 수 있으므로 D(G(z))는 0이 되어 두번째 항은 log(1-0)=log1=0이 되어 전체 식 V(D,G) = 0이 됩니다. 즉 D의 입장에서 얻을 수 있는 이상적인 결과, '최댓값'은 0임을 확인 할 수 있습니다.

그 다음 G의 입장에서 이 value function V(D,G)의 이상적 결과를 생각해보면, G가 D가 구별못할만큼 진짜같은 데이터를 잘 생성해낸다고 했을 때, 첫번째 항은 D가 구별해내는 것에 대한 항으로 G의 성능에 의해 결정될 수 있는 항이 아니므로 넘어가고 두번째 항을 살펴보면 G가 생성해낸 데이터는 D를 속일 수 있는 성능이라 가정했기 때문에 D가 G가 생성해낸 이미지를 가짜라고 인식하지 못하고 진짜라고 결정해버립니다. 따라서 D(G(z)) =1이 되고 $log(1-1)=log0=-\infty$ 가 된다. 즉, G의 입장에서 얻을 수 있는 이상적인 결과, '최솟값'은 $-\infty$ 임을 확인할 수 있습니다.

따라서 D는 training data의 sample과 G의 sample에 진짜인지 가짜인지 올바른 라벨을 지정할 확률을 최대화하기 위해 학습하고, G는 log(1-D(G(z))를 최소화(D(G(z))를 최대화)하기 위해 학습되는 것이죠 !
D입장에서는 V(D,G)를 최대화시키려고, G입장에서는 V(D,G)를 최소화 시키려고 하고, 논문에서는 D와 G를 V(G,D)를 갖는 two-player minmax game 으로 표현하였습니다.

훈련을 진행할 때, inner loop에서 D를 최적화하는 것은 많은 계산들을 필요로 하고 유한한 데이터셋에서는 overfitting을 발생시키기에, k step 만큼 D를 최적화하고 G는 1 step 만큼 최적화하도록 진행합니다.

학습 초반에는 G의 성능이 형편없기 때문에 D가 G가 생성해낸 데이터와 실제 데이터 샘플을 너무 잘 구별해버립니다. 이런 경우에는 log(1-D(G(z))가 포화상태가 되므로 log(1-D(G(z))를 최소화하려고 하는 것보다 log(D(G(z))를 최대화되게끔 학습하는 것이 더 좋다고하는데요, G가 형편없을 때에는 log(1-D(G(z))의 gradient를 계산했을 때 너무 작은 값이 나오므로 학습이 느리기 때문입니다.

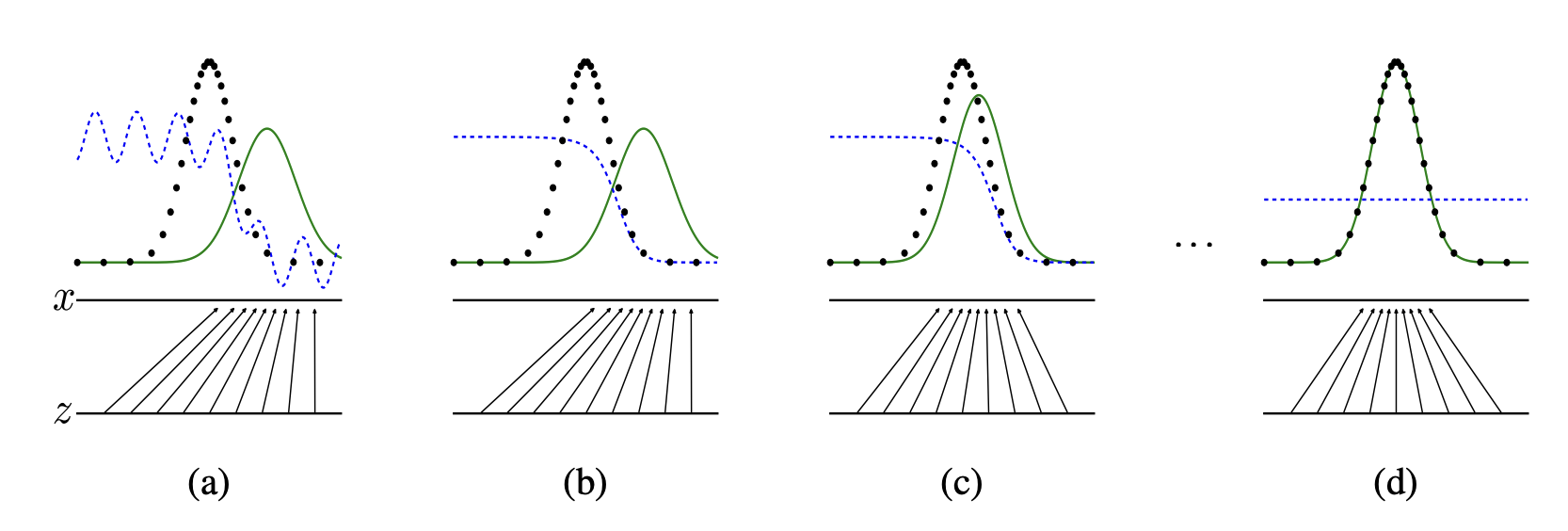
위의 그림에서

파란색 점선: discriminative distribution (분별자 분포)
검은색 점선: data generating distribution(real) (실제 데이터)
녹색 실선: generative distribution(fake) (가짜 데이터)

GAN의 학습과정을 나타낸 이미지를 확인해봅시다.

(a) 학습초기에는 real과 fake의 분포가 전혀 다른 모습이죠. (학습이 안되었기 때문에) D의 성능도 좋지 않은 것도 확인할 수 있습니다.
(b) D가 (a)처럼 들쑥날쑥하게 확률을 판단하지 않고, 흔들리지 않고 real과 fake를 분명하게 판별해내고 있음을 확인할 수 있습니다. 이것은 D의 성능이 올라갔다는 것을 나타냅니다.
(c) 어느정도 D가 학습이 이루어지면, G는 실제 데이터의 분포를 모사하며 D가 구별하기 힘든 방향으로 학습을 하여 녹색과 검은색 점선이 비슷하게 따라가는 것을 볼 수 있습니다.
(d) 이 과정을 반복하게되면 real과 fake의 분포가 거의 비슷해져 구분할 수 없을 만큼 G가 학습을 하게되며, D가 이 둘을 구분할 수 없게 되어 확률을 1/2로 계산하게 됩니다.

이 과정을 통해 진짜와 가짜 데이터를 구별할 수 없을 만한 데이터를 G가 생성해내고 이것이 GAN의 결과물이라고 볼 수 있게됩니다.

Theoretical Results

이 부분에서는 위에서 제시된 GAN의 minmax problem이 제대로 작동한다면, minmax problem이 global minimum에서 unique solution 을 가지고 어떠한 조건에 만족하면 그 solution으로 수렴한다는 사실이 증명되어야 한다는 것을 수학적으로 입증하고 있습니다.

Global Optimality of $P_g = P_{data}$

Proposition 1. G 가 고정된 경우에, 최적의 discriminator D 는?

D^*_G(x) = \frac{P_{data}(x)}{P_{data}(x)+P_g(x)}

G가 고정되어 주어진다면, D 는 위의 수식과 같이 V(G,D)를 최대화하려합니다.

V(G,D) = \int_{x} P_{data}(x)log(D(x))\, dx + \int_{z} P_z(z)log(1-D(G(x)))\, dz \\ \ \\ = \int_{x} [P_{data}(x)log(D(x))+P_g(x)log(1-D(x))]\, dx

$(a,b) \in \mathbb{R}^2 \ \left\{ 0,0 \right\}$ 이 아닌 실수 순서쌍(a,b) 에 대해서 함수 $y \to alog(y) + blog(1-y)$ 이를 미분하고 최댓값인 경우를 계산하면

두번째로 나오는 정의는
The global minimum of the virtual training criterion C(G) is achieved if and only if $P_g = P_{data}$ . At that point, C(G) achieves the value $-log4$ .

이를 증명해봅시다.
$P_g = P_{data}$ 인 $P_g$ 에 대하여 $D^*_G = \frac{1}{2}$ 이므로, C(G) 에 대입을 하면 $log\frac{1}{2}+log\frac{1}{2} = -log4$ 가 됩니다. 이 값이 C(G) 의 최솟값임을 증명하는 것이죠.

위의 증명을 통해 C(G) = $-log4$ 가 C(G) 의 minimum 이며, unique solution 은 $P_g = P_{data}$ 가 됩니다.

이는 data generating process를 완벽히 복제하는 generative model 인 것이 입증됩니다.

Convergence of Algorithm 1

이 알고리즘이 문제를 잘 해결하는지를 증명하는 과정입니다.

Proposition 2. G,D 가 충분한 용량을 가지고 있고, algorithm 이 각 step 에서 discriminator 가 주어진 G 에 대하여 optimum 에 도달할 수 있ㄷ록 허용하고, $P_g$ 가 업데이트되어 기준을 개선한다면,

\mathbb{E}_{x\sim{p_{data}(x)}}[logD(x)] + \mathbb{E}_{x\sim{p_g}}[log(1-D^*_{G(x)})]

의 $P_g$ 는 $P_{data}$ 로 수렴합니다.

증명해보면,
$V(G,D) = V(P_g, D)$ 를 $P_g$ 의 함수로 생각하면, $V(P_g, D)$ 는 $P_g$ 에서 정점(최대값의 도함수) 를 찍습니다.

여기서 만약 $f(P_g) = sup_{p \in D}f_D(P_g)$ 이고 $f_D(P_g)$ 가 모든 D 마다 $P_g$ 에서 정점을 찍는다면, 대응하는 G가 주어진 최적의 D 에서 $P_g$ 에 대한 gradient - descent update 와 동일합니다.

따라서 $P_g$ 에 대한 적은 수의 update 만으로도 $P_g \to P_{data}$ 에 수렴하는 것입니다.

따라서 알고리즘이 global optimal 을 찾아주는 것도 입증하였습니다.

Experiments

본 논문에서는 MNIST, Toronto Face Database(TFD), CIFAR-10에 대해 학습을 진행하였으며,

G는 rectifier linear activations, sigmoid 혼합하여 사용하였고, D는 maxout activation을 사용하였습니다. 또한 D를 학습시킬 때 Dropout을 사용하였습니다.

Advantages and disadvantages

장점과 단점을 정리해보면,

장점은

Markov chains이 전혀 필요 없고 gradients를 얻기 위해 back-propagation만이 사용되었습니다.

학습 중 어떠한 inference가 필요 없습니다.

다양한 함수들이 모델이 접목될 수 있습니다.

Markov chains을 쓸 때보다 훨씬 선명한 이미지를 얻을 수 있다고 합니다.

단점은

$p_g(x)$ 가 명시적으로 존재하지 않습니다.

D와 G가 균형을 잘 맞춰져서 성능이 향상되어야 한다는 점입니다. (G는 D가 너무 발전하기 전에 너무 발전되어서는 안되며, G가 z 데이터를 너무 많이 붕괴시켜버리기 때문입니다.)

Conclusions and future work

본 논문의 개념은 conditional generative model 로 발전시킬 수 있음을 밝혔으며,(CGAN)

Learned approximate inference는 주어진 x를 예측하여 수행될 수 있다고 합니다. 또한 parameters를 공유하는 conditionals model를 학습함으로써 다른 conditionals models을 근사적으로 모델링할 수 있습니다.

특히 MP-DBM의 stochastic extension의 구현 에 대부분의 네트워크를 사용할 수 있다고합니다. 추가적으로 개선안은

Semi-supervised learning: 제한된 레이블이 있는 데이터 사용할 수 있을 때, classifiers의 성능 향상시킬 수 있으며,
효율성 개선: G,D를 조정하는 더 나은 방법이나 학습하는 동안 sample z에 대한 더 나은 분포를 결정함으로써 학습의 속도 높일 수 있습니다.

Generative Adversarial Nets - 논문 보기

코넬

어서오세요.

이전 포스트