[C++] 백준 10844. 쉬운 계단 수

멋진감자·2025년 2월 2일

DP boj cpp

알고리즘

목록 보기

76/117

🌽 문제

🥕 입출력

🥔 풀이

dp 문제니까 냅다 적어보면서 규칙을 찾아보려고 했다.
n = 4까지 적어보니 아래 식이 성립하길래 냅다 제출해봤다.

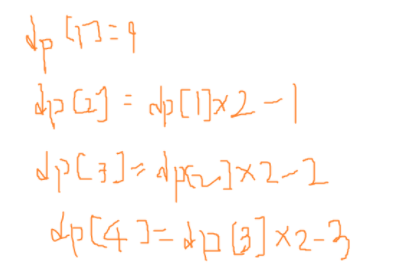
음 틀렸고
한 일주일 전에 풀었던 계단 문제가 생각나서 거꾸로 생각해보기로 했다.
위에 저 공식을 낼 때는 첫 자리가 1인 것부터 시작했었는데
이번엔 마지막 자리에 집중했다.

자릿수가 1인 경우는 1부터 9까지 총 9개이다.
끝자리 숫자의 관점에서 0을 제외한 수, 1~9로 끝나는 경우는 모두 1이다.

자릿수가 2일 때, 끝자리 숫자 관점으로 생각해보자.
0으로 끝나는 수는 앞에 1만 올 수 있다.
1로 끝나는 수는 앞에 0과 2가 올 수 있다.
2로 끝나는 수는 앞에 1과 3이 올 수 있다.
..
9로 끝나는 수는 앞에 8만 올 수 있다.

자 이번에는 자릿수가 3일 때, 끝자리 숫자 관점에서 보자.
0으로 끝나는 수는 앞에 1로 끝나는 두 자리 수의 경우의 수만큼 올 수 있다.
1로 끝나는 수는 앞에 0또는 2로 끝나는 두 자리 수의 경우의 수만큼 올 수 있다.
..
9로 끝나는 수는 앞에 8로 끝나는 두 자리 수의 경우의 수만큼 올 수 있다.

이 정도까지 생각했으면 문제를 못 풀기가 어렵다.
2차원의 dp 배열을 두고, dp[i][j]에서 i는 자릿수, j를 끝나는 수로 놓고 풀면 된다.

풀다보니 왠지 과거에 이 문제를 풀어본 것 같다고 생각했다.
기분탓인가

🥬 코드

#include <iostream>
using namespace std;

#define N 1000000000

int n;
int dp[101][10];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n;
	for (int i = 1; i <= 9; i++) {
		dp[1][i] = 1;
	}
	for (int i = 2; i <= n; i++) {
		for (int j = 0; j <= 9; j++) {
			if (j == 0) dp[i][j] = dp[i - 1][1] % N;
			else if (j == 9) dp[i][j] = dp[i - 1][8] % N;
			else dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j + 1]) % N;
		}
	}
	long long sum = 0;
	for (int i = 0; i <= 9; i++) {
		sum += dp[n][i];
	}
	cout << sum % N;
	return 0;
}