[C++] 백준 1934. 최소공배수

멋진감자·어제

C GCD LCM boj

알고리즘

목록 보기

16/20

문제

t개의 a와 b가 주어질 때, a, b의 최소공배수를 출력하는 문제이다.

흠

최소공배수 최대공약수 소수 이런거 비교적 최근에 풀었던건데
알고리즘 이름(유클리드 호제법)만 기억나서 당황스럽다.
당황스러우면 어쩔건데 빨리 공부해
넵

유클리드 호제법

어떤 두 정수 a, b(a > b, a != b)의 최대공약수를 gcd(a, b)라 하자.
여기서 gcd는 greatest common divisor의 약자이고
이따 나올 lcm은 least common multiple의 약자다.

gcd(a, b) = gcd(b, a % b)가 바로 유클리드 호제법이다.
위 식이 성립하므로 우항이 gcd(a % b, b % (a % b))도 될 수 있다.

이걸 반복하다보면 오른쪽 수가 0이 되는 순간(gcd(?, 0))이 온다.
왼쪽수의 가장 큰 약수는 왼쪽수 자신이 되고,
0의 약수는 모든 정수이므로,
두 수의 최대공약수는 결국 왼쪽수가 된다.

풀이

최소공배수를 구하는 문제에 최대공약수는 무슨일이냐 물으신다면
대답해 드리는 게 인ㅈ

어릴 때 기억을 더듬어보면 최대공약수 또는 최소공배수를 구할 때
아래 이미지처럼 니은자를 쳐가며 무한 나누기를 했더랬다.

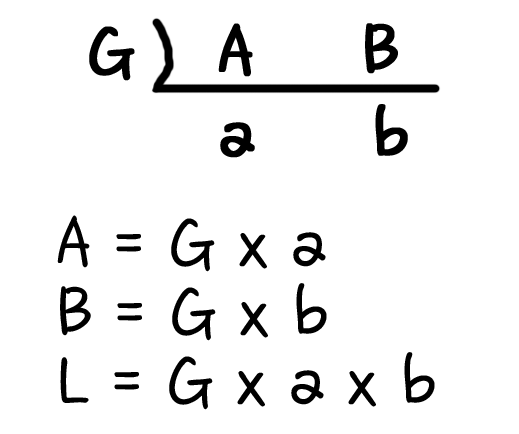
G는 최대공약수, L은 최소공배수다.
이렇게 문자로 정리된 A와 B를 곱해보면

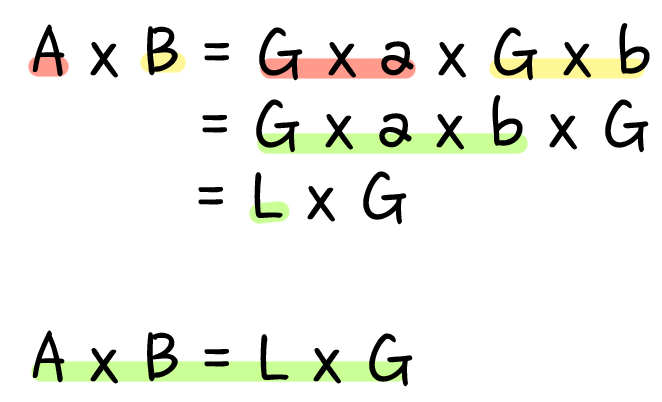
최소공배수는 두 수의 곱을 최대공약수로 나눈 값임을 알 수 있다.
고대로 코드로 옮겨주면 된다.

코드

if (a % b == 0) return b;로 연산이 한 단계 덜 가도록 만들었는데
if (b == 0) return a;랑 그게 그거다.

#include <iostream>

using namespace std;

int gcd(int a, int b) {
	if (a % b == 0) return b;
	else return gcd(b, a % b);
}

int lcm(int a, int b) {
	return a * b / gcd(a, b);
}

int main() {
	int t, a, b, ans;
	cin >> t;
	for (int i = 0; i < t; i++) {
		cin >> a >> b;
		if (a == b) ans = a;
		else if (a == 1) ans = b;
		else if (b == 1) ans = a;
		else {
			if (a < b) {
				int tmp = a;
				a = b;
				b = tmp;
			}
			ans = lcm(a, b);
		}
		cout << ans << "\n";
	}

	return 0;
}