Paging

Linear Tables

대부분 각 process는 하나의 page table을 갖고 있다.

만약 4-KiB page로 이루어진 32-bit address space가 있고 4-byte page entry를 가지고 있다면

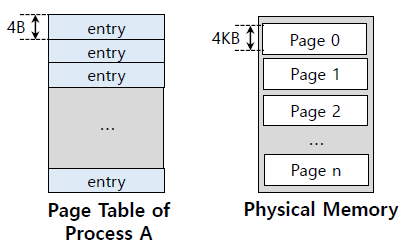
(page table size) = (2^32)/(2^12) * (4-Byte) = 4MB

page table의 크기가 너무 크기 때문에 모든 process에 대해서 4MB의 page table을 할당하기에는 너무 많은 memory를 소모하게 된다.

Smaller Tables

만약 16-KiB page로 이루어진 32-bit address space가 있고 4-byte page entry를 가지고 있다면

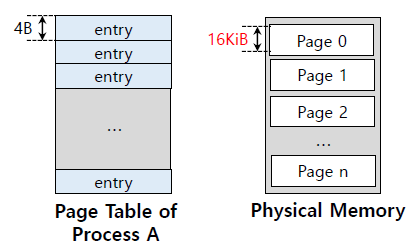
(page table size) = (2^32)/(2^16) * (4-Byte) = 1MB

page의 크기를 키우니까 page table의 크기가 줄어들었다.
하지만 big page는 internal fragmentation을 유발할 수 있다.
page table의 많은 entry를 실제로 사용하지 않음에도 page table의 공간으로 할당하고 있어야하기 때문이다.

The Core Problem

process의 전체 address space에 대해 single page table을 사용했을 때의 문제점은 다음과 같다.
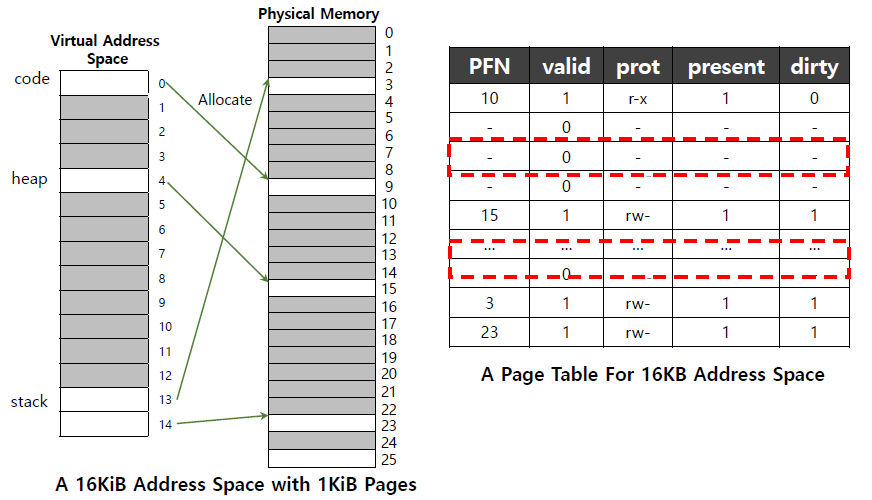page table의 대부분이 unused이며 invalid한 entry라는 것이다.
이미 할당된 공간이라 외부에서 다른 용도로 사용할 수는 없지만 실제로 사용되는 공간이 아니어서 unused상태로 남게 되는 것이다. single, contiguous, fixed-size address space를 사용하면 fragmentation이 발생했던 것과 같은 상황이다.

그래서 다시 segment memory model을 page table에 적용하자는 것!
address space나 virtual address space는 이미 paging을 통해 해결이 된 상태니 page table의 internal fragmentation 문제만 해결해주면 된다.

Hybrid Approach: Paging and Segments

page table의 memory overhead를 줄이기 위해 base가 자신의 segment를 가리키는 것이 아닌 그 segment의 page table의 physical address를 가리키게 하고 bound register가 그 page table의 end를 가리키도록 한다.

예를 들어 각 process가 3개의 page table을 갖도록 만들 수 있다.
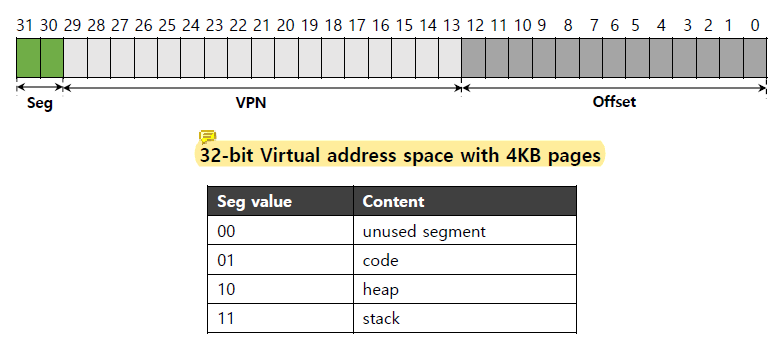4KB page까지는 좋았는데 남은 20-bits를 contiguous하게 할당하는게 문제인 것이다.
하나의 연속적이었던 영역을 여러 개의 작은 연속적인 영역으로 바꾸는 것이다. segmented page table.

Problem of Hybrid Approach

hybrid approach도 문제가 없진 않다.

만약 우리가 크고 sparsely-used heap을 사용한다면 많은 page table을 낭비하게 된다.
external fragmentation 문제가 다시 발생한다.

segmented memory model을 사용하면 각 segment는 여전히 contiguous하고 서로 다른 size를 갖고 있으므로 external fragmentation이 발생한다.

Multi-level Page Tables

paging을 page table에 recursive하게 적용한다.

Page Directroy

page table을 page-sized unit으로 자른다.
page table entry의 전체가 invalid하다면 그 page table의 해당 page도 allocte하지 않는다.

page table의 그 page가 valid한지 track하기 위해서는 page directory라는 새로운 structure를 사용해야함.

page directory의 각 entry는 chopped page table(segment)의 base address를 담고 있다.
만약 chopped page table을 사용하지 않는다면 allocate하지 않는다. page directory에서 invalid한 entry에 해당하는 page table은 allocate하지 않는다는 것이다.

그럼에도 page directory가 아직도 크게 느껴진다면 page directory를 다시 쪼개서 paging을 적용하면 된다.
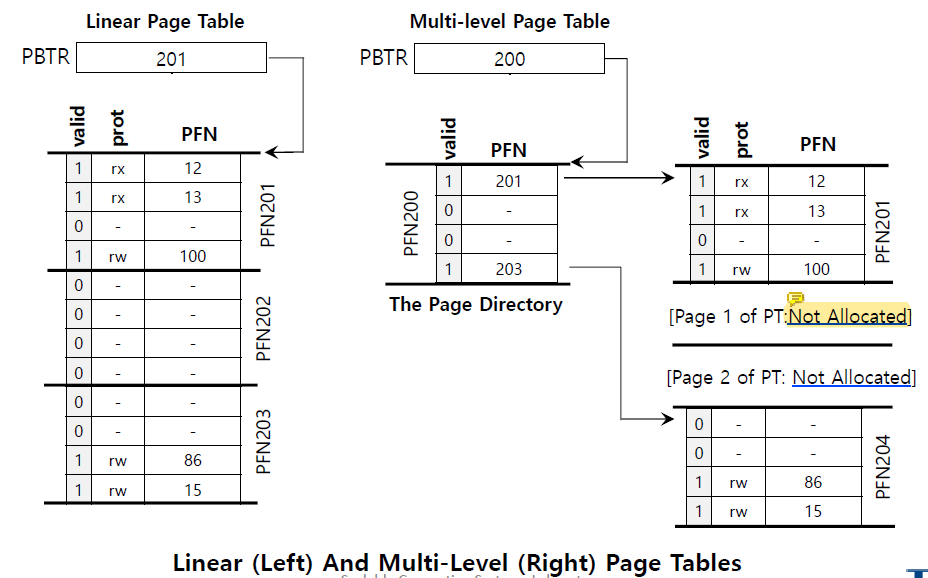invalid한 page directory에 해당하는 page table은 할당하지 않기 때문에 page table의 크기를 줄일 수 있다.

Page Directory Entries

page directory에는 page table의 각 page당 하나의 entry가 있다.
이것은 몇 개의 page directory entry(PDE)로 구성되어 있다.

PDE는 valid bit과 page table의 page frame number(PFN)으로 이루어져 있다.

Advantage & Disadvantage

• Advantages

  • 사용하는 address space에 해당하는 부분만 page table을 할당할 수 있다. high utilization.
  • OS가 allocate나 page table 증가를 위해 다음 free page를 이용하면 된다.

• Disadvantages

  • time-space trade-off 관계이다.
    lookup cost가 증가한다. page table을 하나만 보면 되는게 아니라 여러 개를 봐야하기 때문이다. address translation time 증가. level이 많을 수록 더 많은 시간이 소요된다.
  • complex.

A Detailed Milti-Level Example

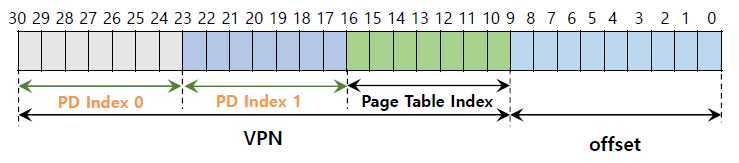
address space가 16KiB이므로 2^4 * 2^10으로 14-bits이다.
page size가 64bytes이므로 6-bits이다. 따라서 offset도 6-bits이다.
VPN은 14-6 = 8-bits이다.

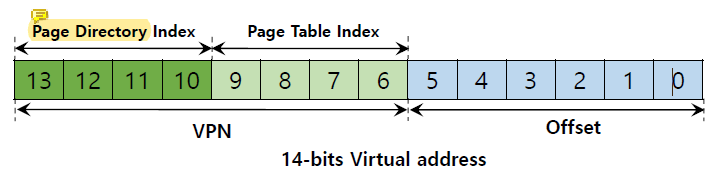
page directory는 page table의 page마다 한 entry를 가진다.
page directory의 entry가 invalid하면 exception을 발생시킨다.

page directory entry(PDE)가 valid하다면 이 PDE가 가리키는 page table의 page에서 page table entry(PTE)를 가져온다.
그때부터 page-table index를 그 page table을 가리키는 index로 사용할 수 있다.

page directory는 반드시 모두 할당되어야 한다. 그게 root이기 때문.

More than Two Level

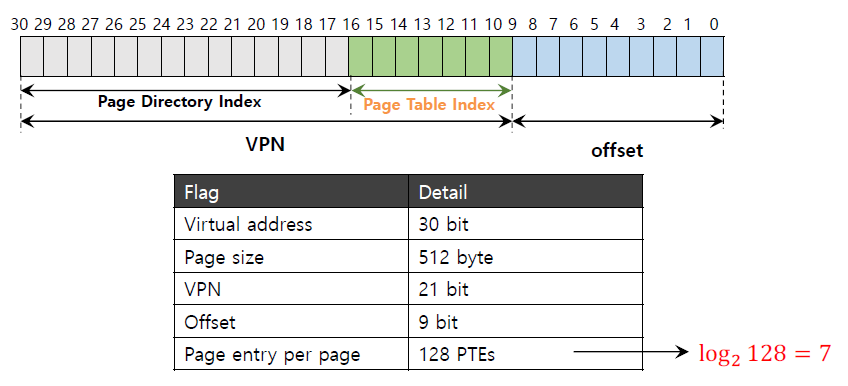page size 512 byte = 9-bits이다. 따라서 offset이 9-bits, VPN이 30-9 = 21-bits 가 된다.

여기서 좀 더 쪼개면 7-bits를 이용해 page 당 page entry를 128 PTE로 조절할 수 있다.
만약 page directory가 2^14 entry를 가지고 있다면 이 page directory는 한 page에 해당하는 것이 아니라 128 page에 span됨.

이 문제를 개선하기 위해 page directory를 더 쪼개서 further level의 tree를 만든다.

Multilevel Paging

The Two-Level Page Table

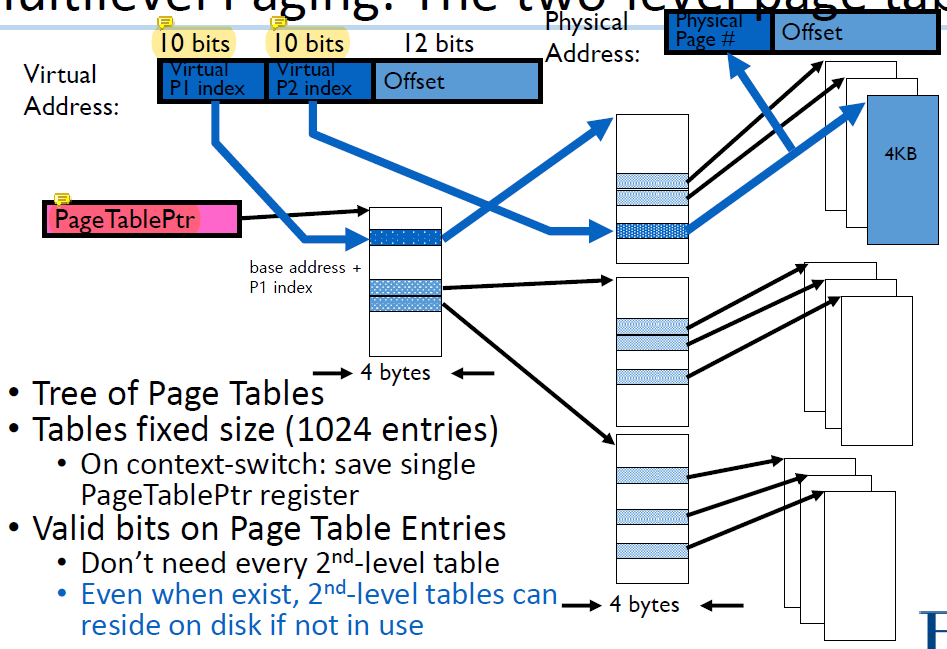가장 상위 10bit는 base page directory에서 어떤 entry를 선택해야 하는지 알려준다.
CR3에 있는 base address에 virtual P1 index가 나타내는 offset을 더한 위치의 entry로 이동한다.

그 다음 10bit는 page table에서 어떤 entry를 사용해야 하는지 결정한다.
여기에서는 PFN을 찾는다. final page를 찾을 수 있다.

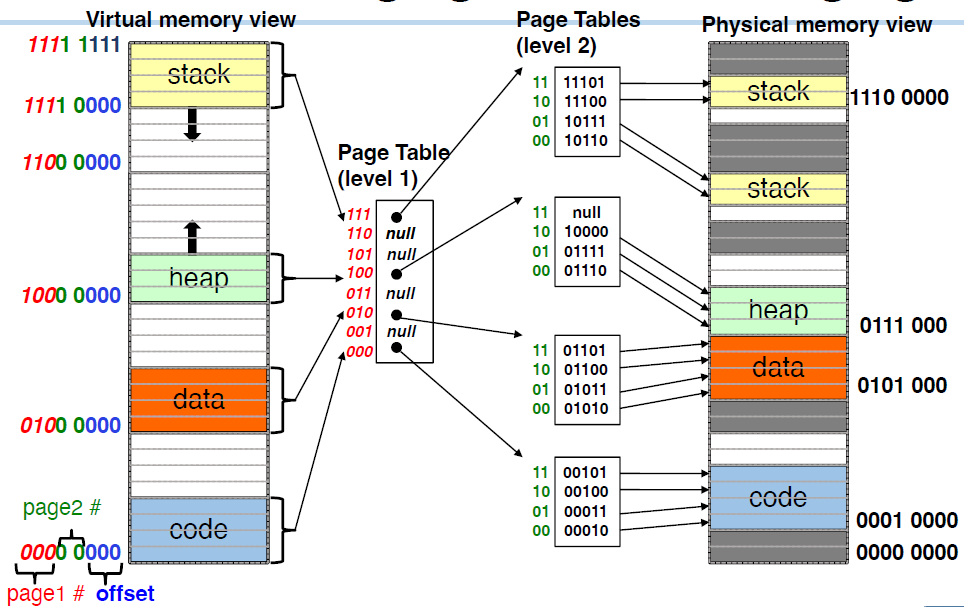
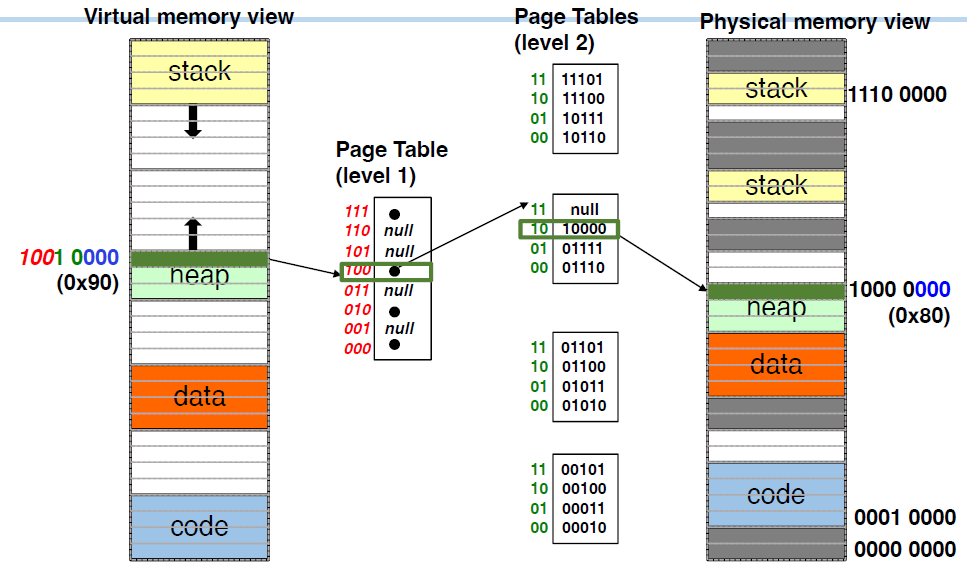
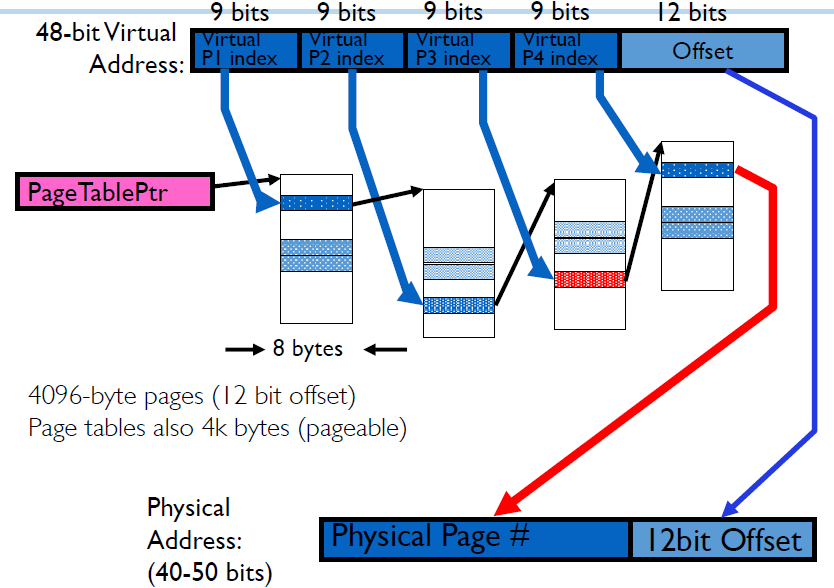
The Four-Level Page Table

Nested Paging For Virtual Machines