108. 개미 전사

• 개미 전사는 부족한 식량을 충당하고자 메뚜기 마을의 식량창고를 몰래 공격하려고 한다.

• 메뚜기 마을에는 여러 개의 식량 창고가 있는데 식량 창고는 일직선으로 이어져 있다.

  • 각 식량 창고에는 정해진 수의 식량을 저장하고 있으며 개미 전사는 식량 창고를 선택적으로 약탈하여 식량을 빼앗을 예정이다.

• 이때 메뚜기 정찰병들은 일직선상에 존재하는 식량창고 중에서 서로 인접한 식량 창고가 공격받으면 바로 알아챌 수 있다.

  • 따라서 개미 전사가 정찰병에게 들키지 않고 식량 창고를 약탈하기 위해서는 최소한 한 칸 이상 떨어진 식량 창고를 약탈해야 한다.

예를 들어 식량 창고 4개가 다음과 같이 존재한다고 가정하자.
{1, 3, 1, 5}


이때 개미 전사는 두 번째 식량 창고와 네 번째 식량창고를 선택했을 때 최댓값인 총 8개의 식량을 빼앗을 수 있다.

• 개미 전사는 식량 창고가 이렇게 일직선상일 때 최대한 많은 식량을 얻기를 원한다.

• 개미 전사를 위해 식량 창고 N개에 대한 정보가 주어졌을 때 얻을 수 이쓴 식량의 최댓값을 구하는 프로그램을 작성하시오.

• 입력조건

  • 첫째 줄에 식량창고의 개수 N이 주어진다. (3 ≤ N ≤ 100)

  • 둘째 줄에 공백으로 구분되어 각 식량창고에 저장된 식량의 개수 K가 주어진다. (0 ≤ K ≤ 1,000)

• 출력조건

  • 첫째 줄에 개미 전사가 얻을 수 있는 식량의 최댓값을 출력하시오.

1. 타뷸레이션을 이용한 풀이

n = int(input())

array = list(map(int, input().split()))

d = [0] * 100

d[0] = array[0]
d[1] = max(array[0], array[1])
for i in range(2, n):
  d[i] = max(d[i - 1], d[i - 2] + array[i])

print(d[n-1])

• 이 문제의 점화식을 한 번 세워보자

  • 왼쪽부터 차례대로 식량창고를 털지 안 털지를 결정하는 경우,
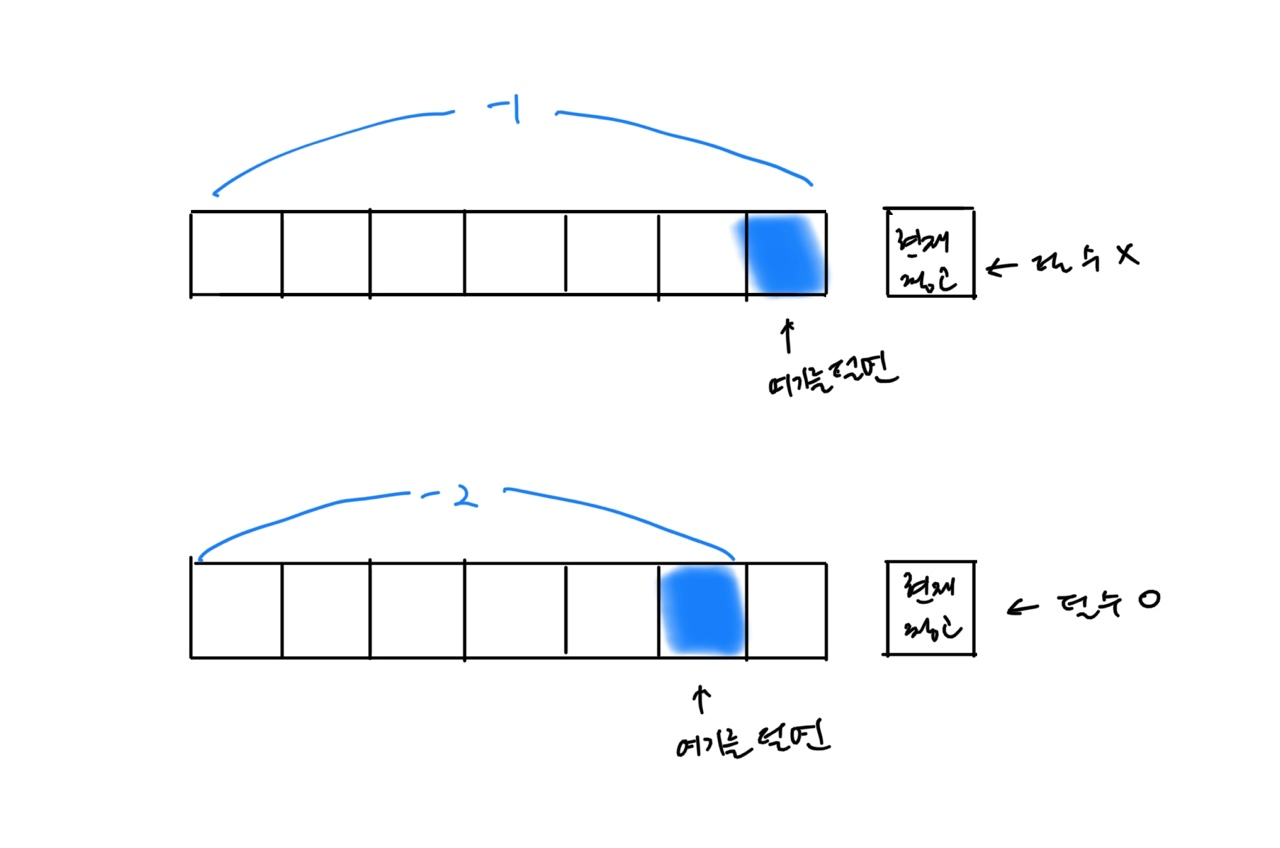
    특정한 i번째 식량 창고에 대해서 털지 안 털지의 여부를 결정할 때,

    단 2가지 경우에 대해서만 확인하면 된다.
    
    
    1) (i - 1)번째 식량창고를 털기로 결정한 경우 현재의 식량창고를 털 수 없다.
    
    2) (i - 2)번째 식량창고를 털기로 결정한 경우 현재의 식량창고를 털 수 없다.

  

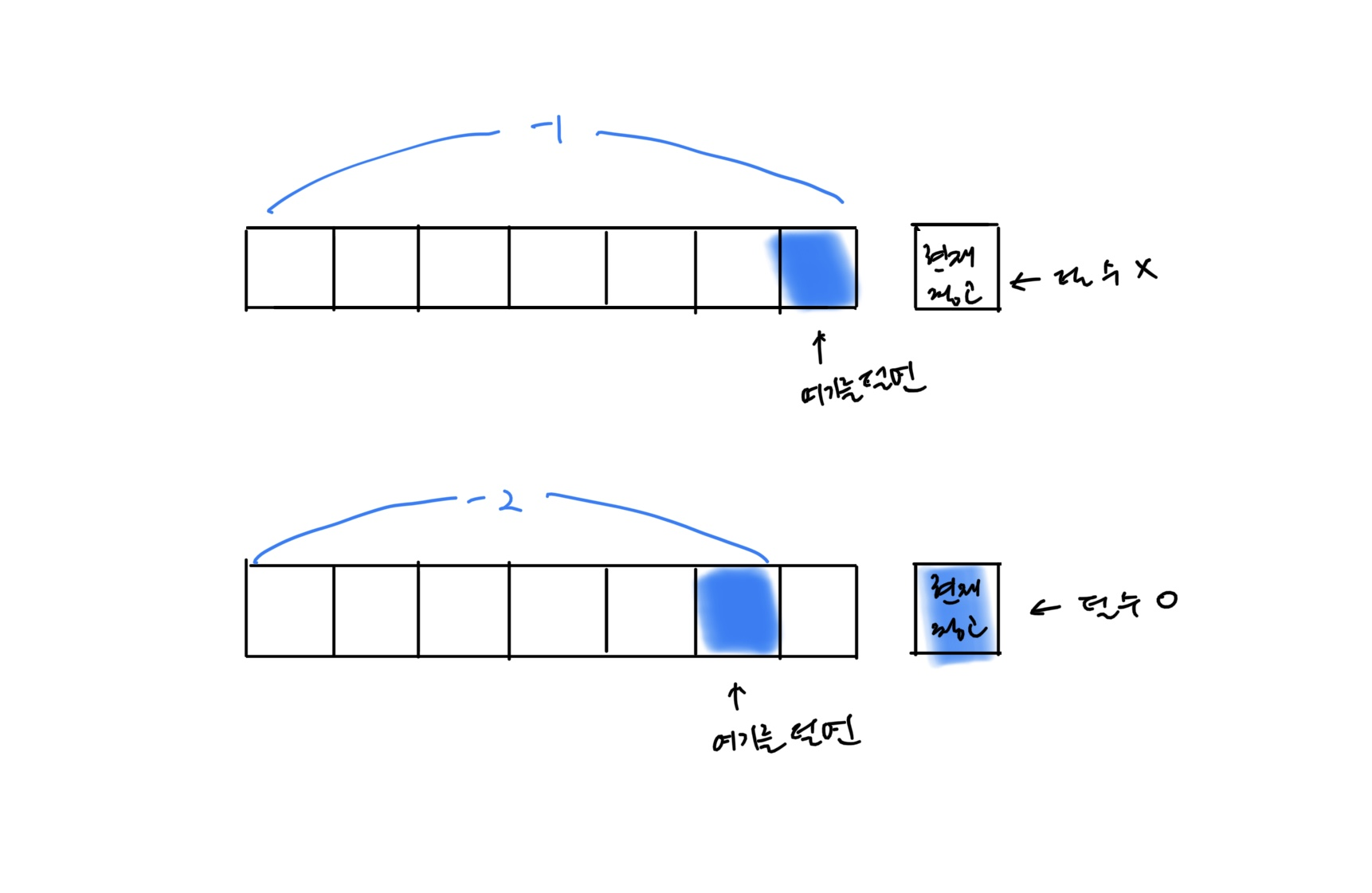
  • 따라서, 1)과 2) 중에서 더 많은 식량을 털 수 있는 경우를 선택하면 된다.

• 여기서 i번째 식량창고에 대한 최적의 해를 구할 때 왼쪽부터 (i - 3)번째 이하의 식량 창고에 대한 최적의 해에 대해서는 고려할 필요가 없다는 점이다.

  • 예를 들어 d[i - 3]는 d[i - 1]과 d[i - 2]을 구하는 과정에서 이미 계산되었기 (고려되었기) 때문에, d[i]의 값을 구할 때는 d[i - 1]과 d[i - 2]만 고려하면 된다.

  • 따라서 i번째 식량 창고에 있는 식량의 양이 kᵢ라고 했을 때 점화식은 다음과 같다.

    aᵢ = max(aᵢ₋₁,aᵢ₋₂+ kᵢ)

2. C++ 코드

#include <bits/stdc++.h>

using namespace std;

// 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
int d[100];
int n;
vector<int> arr;

int main(void) {
    // 정수 N을 입력받기
    cin >> n;
    // 모든 식량 정보 입력받기
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        arr.push_back(x);
    }

    // 다이나믹 프로그래밍(Dynamic Programming) 진행(보텀업)
    d[0] = arr[0];
    d[1] = max(arr[0], arr[1]);
    for (int i = 2; i < n; i++) {
        d[i] = max(d[i - 1], d[i - 2] + arr[i]);
    }

    // 계산된 결과 출력
    cout << d[n - 1] << '\n';
}

3. Java 코드

import java.util.*;

public class Main {

    // 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화 
    public static int[] d = new int[100];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        // 정수 N을 입력받기
        int n = sc.nextInt();

        // 모든 식량 정보 입력받기
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = sc.nextInt();
        }
        
        // 다이나믹 프로그래밍(Dynamic Programming) 진행(보텀업)
        d[0] = arr[0];
        d[1] = Math.max(arr[0], arr[1]);
        for (int i = 2; i < n; i++) {
            d[i] = Math.max(d[i - 1], d[i - 2] + arr[i]);
        }

        // 계산된 결과 출력
        System.out.println(d[n - 1]);
    }
}