-
가로의 길이가
N, 세로의 길이가2인 직사각형 형태의 얇은 바닥이 있다. -
태일이는 이 얇은 바닥을
1 X 2의 덮개,2 X 1의 덮개,2 X 2의 덮개를 이용해 채우고자 한다.
- 이때 바닥을 채우는 모든 경우의 수를 구하는 프로그램을 작성하시오.
예를 들어
2 X 3크기의 바닥을 채우는 경우의 수는 5가지 이다.
-
입력조건
- 첫째 줄에
N이 주어진다. (1 ≤ N ≤ 1,000)
- 첫째 줄에
-
출력조건
- 첫째 줄에
2 X N크기의 바닥을 채우는 방법의 수를796,796으로 나눈 나머지를 출력하라.
- 첫째 줄에
1. 타뷸레이션을 이용한 풀이
n = int(input())
d = [0]*1001
d[1] = 1
d[2] = 3
for i in range(3, n + 1):
d[i] = (d[i - 1] + 2 * d[i - 2]) % 796796
print(d[n])
-
이 문제도 다이나믹 프로그래밍의 기초 예제에서 빠질 수 없는 타일리 ㅇ문제 유형이다.
-
다이나믹 프로그래밍 문제에서는 종종 결과를 어떤 수로 나눈 결과를 출력하라는 내용이 들어가 있는 경우가 많다.
- 이는 단지 결괏값이 굉장히 커질 수 있기 때문에 그런 것이다.
-
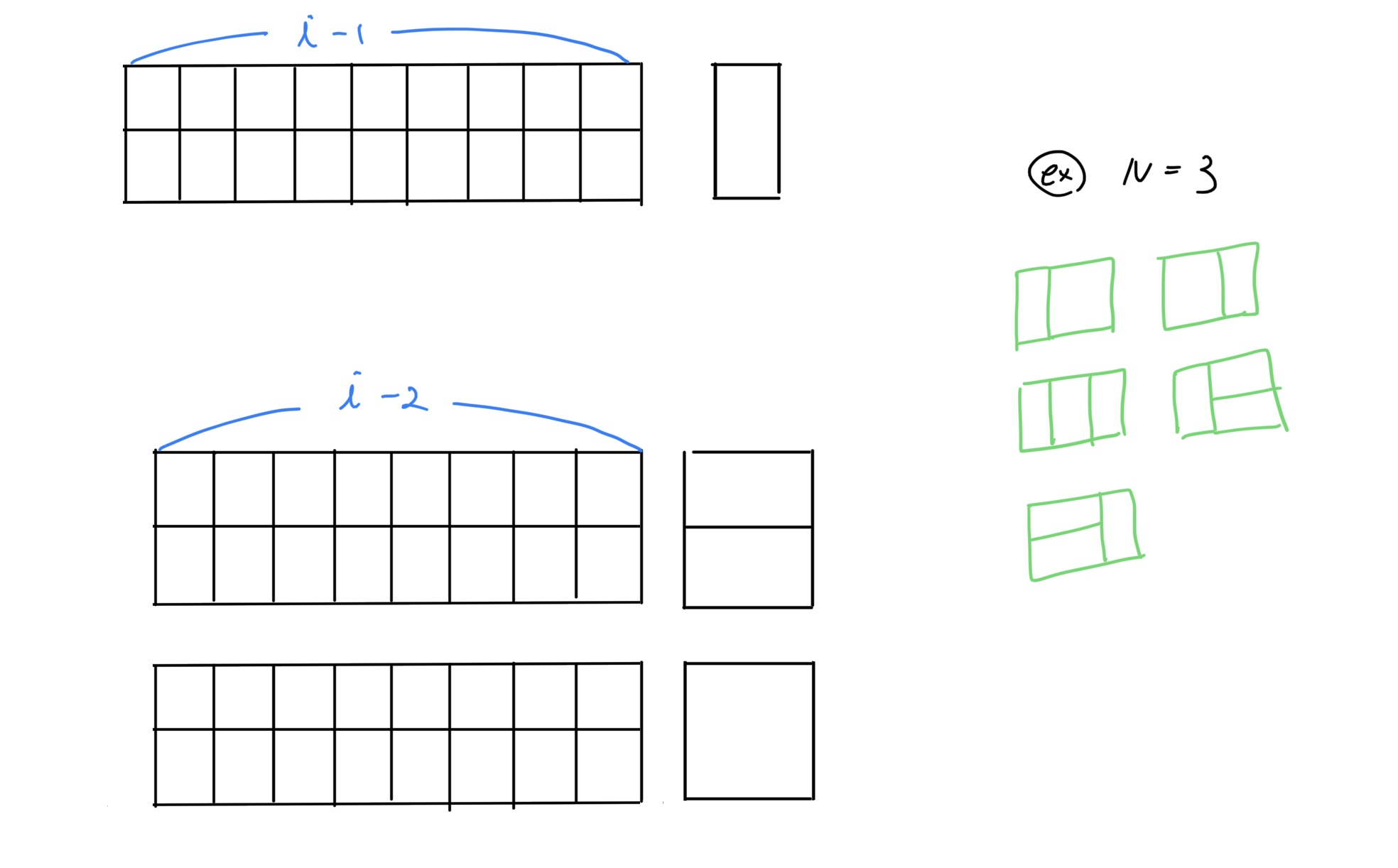
왼쪽부터 차례대로 바닥을 덮개로 채운다고 생각하면 어렵지 않게 점화식을 채울 수 있다.
1) 왼쪽부터
i - 1까지 길이가 덮개로 이미 채워져 있으면2 X 1덮개를 채우는 하나의 경우밖에 존재하지 않는다.2) 왼쪽부터
i - 2까지 길이가 덮개로 이미 채워져 있으면1 X 2덮개 2개를 넣는 경우, 혹은2 X 2의 덮개 하나를 넣는 경우로 2가지 경우가 존재한다.- 참고로
2 X 1덮개 2개를 넣는 경우를 고려하지 않는 것은 1)에서 이미 해당 경우가 고려되었기 때문이다.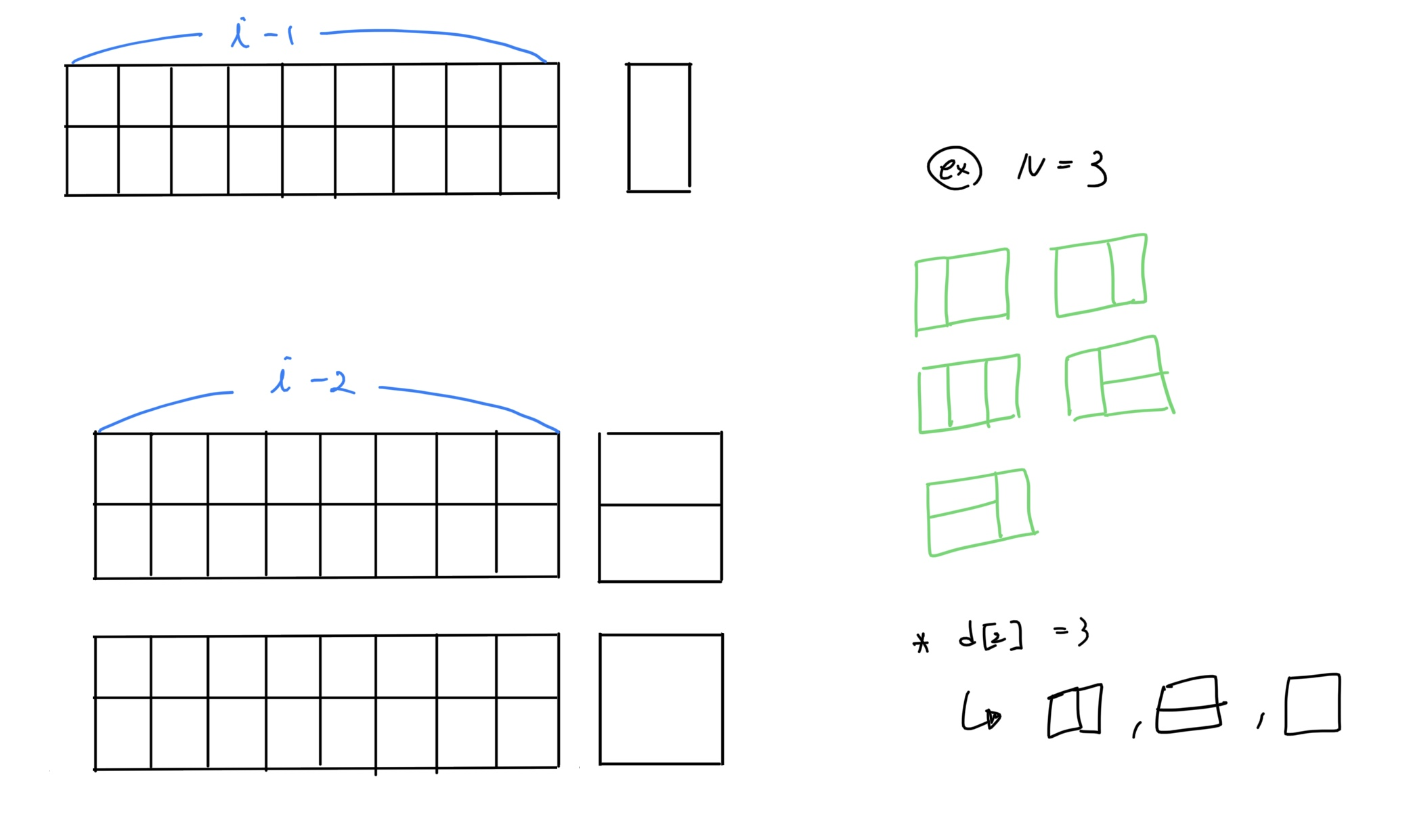
- 참고로
-
최적의 해를 구할 때 왼쪽부터
(i - 3)번째 이하의 위치에 대한 최적의 해에 대해서는 고려할 필요가 없다.-
사용할 수 있는 덮개의 형태가 최대
2 X 2크기의 직사각형 형태이기 때문이다. -
즉, 바닥을 채울 수 있는 형태는 위에서 언급한 경우 밖에 없다.
-
따라서 점화식은 다음과 같다.
aᵢ = aᵢ₋₁ + aᵢ₋₂ x 2
-
-
-
왼쪽부터
N - 2까지 길이가 덮개로 이미 채워져 있는 경우 덮개를 채우는 방법은 2가지 경우가 된다. 이 두 방법은 서로 다른 것이므로, 결과적으로는aᵢ = aᵢ₋₁ + aᵢ₋₂+ aᵢ₋₂가 된다.- 위의 점화식은 이를 간략하게 표현한 것이다.