163. 수학은 너무 쉬워

백준

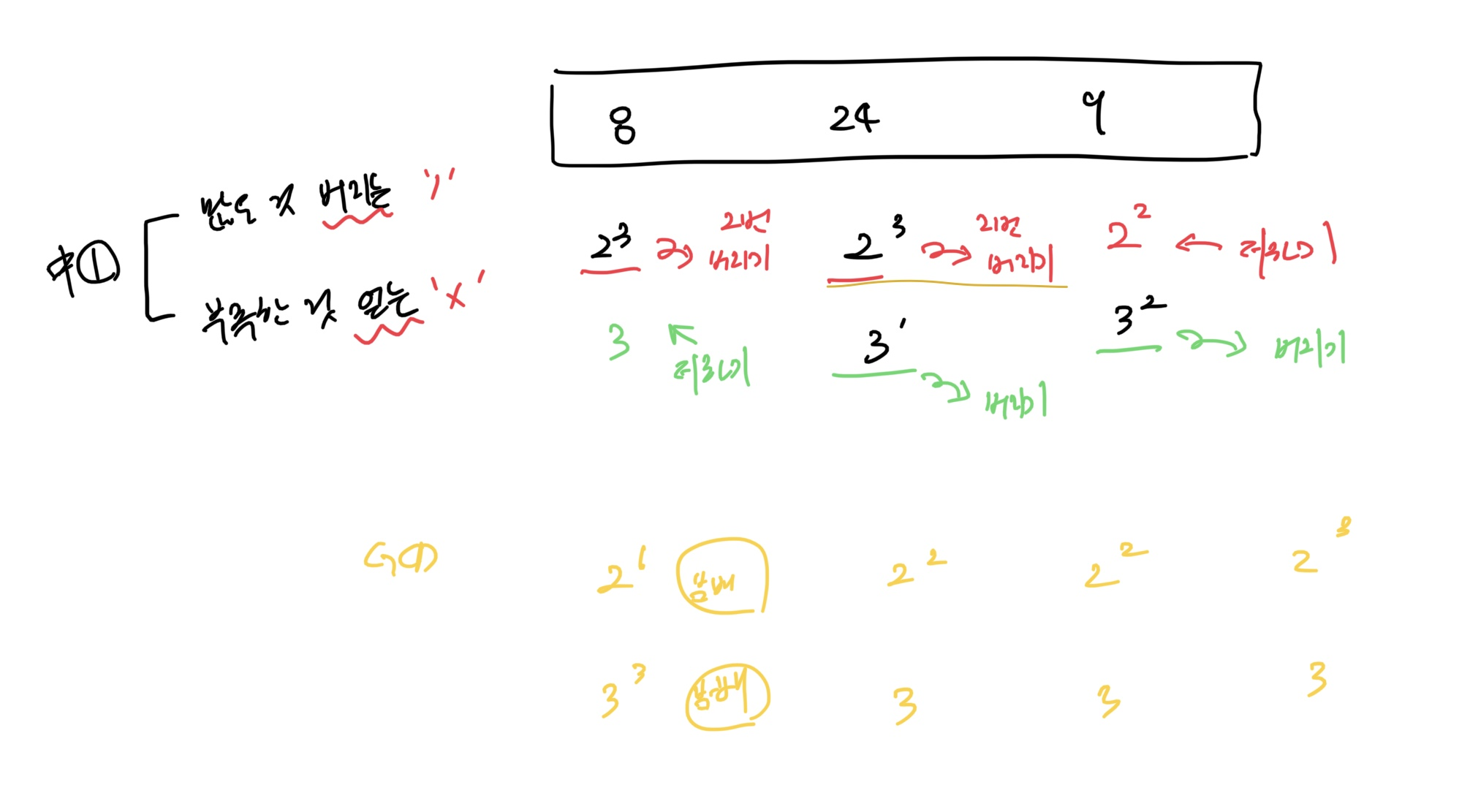
1.Python

2. C++

#include <cstdio>
#include <vector>
using namespace std;

bool che[1000001];
int n, a[100];
vector<int> prime;
int count[100][80000];  // 대략 100만 이하 소수가 7xxxx개 있는데..... 
int totalCount[80000]; //
int gcdCount[80000]; //gcd가 될 것 같은 횟수
int answer1, answer2; //가장 큰 점수, 최소 횟수

int main() {
    for (int i = 2 ; i <= 1000000 ; i++) {
        if (che[i]) continue;
        // i is prime 
        for (int j = i + i ; j <= 1000000 ; j += i) {
            che[j] = true;
        }
    }
    for (int i = 2 ; i <= 1000000 ; i++) {
        if (!che[i]) {
            prime.push_back(i);
        }
    }

    scanf("%d", &n);
    for (int i = 0 ; i < n ; i++) {
        scanf("%d", &a[i]);
    }

    // 각 숫자별로 소수가 몇개씩 있을까????? ==> 소인수분해 
    for (int i = 0 ; i < n ; i++) {
        int num = a[i];
        for (int j = 0 ; j < prime.size() ; j++) {
            while (num % prime[j] == 0) {
                count[i][j]++;
                totalCount[j]++;
                num /= prime[j];
            }
        }
    }
    /*
    // debug
    for (int i = 0 ; i < n ; i++) {
        printf("[%d] : ", a[i]);
        for (int j = 0 ; j < prime.size() ; j++) {
            if (count[i][j] != 0) {
                printf("prime %d %d, ", prime[j], count[i][j]);
            }
        }
        printf("\n");
    }
    */

   
    for (int i = 0; i < prime.size(); i++){
        gcdCount[i] = totalCount[i] / n;
        //n개에다가 분배
    }

    answer1 = 1;
    
    for(int i = 0; i < prime.size();i++){
      for (int j = 0; j < gcdCount[i]; j++){
        answer1 *= prime[i];
      }
      //각 숫자들에 대해서 GCD가 되기 위해서 소수가 얼마나 부족한지 확인
      for (int j = 0; j < n; j++){
        if(count[j][i] < gcdCount[i]){
          answer2 += gcdCount[i] - count[j][i];
        }
      }
    }

    printf("%d %d", answer1, answer2);
    
}