164. 이항 계수 1

백준

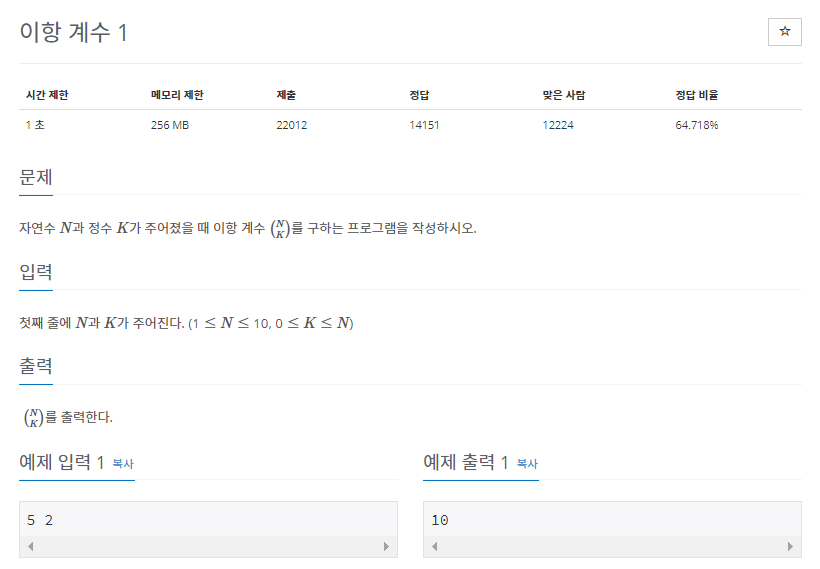
• 이항계수( binomial coefficient ) 는 경우의 수를 계산할때 사용하는 것

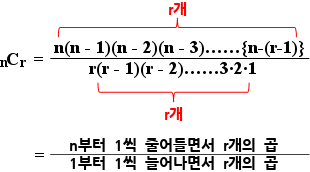
• n개의 서로다른 것 들 중에서 k 개를 선택하는 것의 조합(combination)의 경우의 수를 구하는 것입니다.

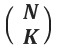
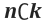
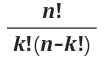
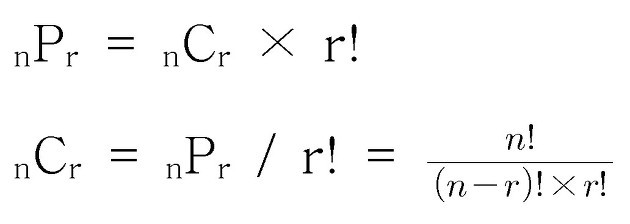
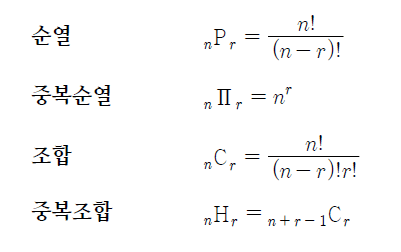
1. Python

n,k=map(int, input().split())
a = 1
b = 1
while k:
    a*=n
    b*=k
    n-=1
    k-=1
print(a//b)

n, k = map(int, input().split())
a = 1
b = 1
for i in range(K):
    a *= (n-i)
    b *= (k-i)

print(a // b)

n,k = map(int, input().split())

def bino_coef(n, k):
    if k == 0 or n == k:
        return 1
    return bino_coef(n-1, k) + bino_coef(n-1, k-1)

print(bino_coef(n, k))

2. C++

다 더해서 나누기

#include<iostream>
 
using namespace std;
 
//반복문 이용. 
int Factorial(int num){
    if(num == 0) return 1;
    
    int result = 1;
    
    for(int i=num; i>=1 ; i--){
        result *= i;
    }
 
    return result;
}
 
 
int main(void){
    
    int n, k;
 
    cin >> n >> k;
 
    cout << Factorial(n) / (Factorial(k) * Factorial(n-k));
    
    return 0;    
}

#include<iostream>
 
using namespace std;
 
//재귀 이용.
int Factorial(int num){
    if(num == 1 || num == 0){
        return 1;
        
    }else{
        return Factorial(num-1) * num;
    }
 
}
 
int main(void){
    
    int n, k;
 
    cin >> n >> k;
 
    cout << Factorial(n) / (Factorial(k) * Factorial(n-k));
    
    return 0;    
}


출처: https://blockdmask.tistory.com/93 [개발자 지망생]

바로 나눠버리기

#include <cstdio>

using namespace std;

int n, k;

int main() {
	scanf("%d%d", &n, &k);

	int ans = 1;
	for (int i = 0; i < k; i++) {
		ans *= n-i;
	}
	for (int i = 1; i <= k; i++) {
		ans /= i;
	}
	printf("%d", ans);
	return 0;
}

#include <cstdio>

int n, k;

int main(){
    scanf("%d%d", &n, &k);

	if(k == 0){
    	printf("%d", 1);
        return 0;
    }

	int p = 1, q = 1;
  int answer = 1;
  for(int i = 1, j = n; i <= k; i++, j--){
    //p *= j;
    //q *= i;  
    //printf("j,i: %d %d\n", j,i);
    
    answer *= j;
    //printf("answer* %d \n", answer);
    answer /= i;
    //printf("answer/ %d \n", answer);
      
  }
  printf("%d", answer);

}

점화식

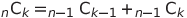
#include <iostream>

//static int binomial로 선언가능.
int binomial(int n, int k)
{
	if (n == k || k == 0) {
		return 1;
	}

	//재귀를 보는 관점 : n-1Ck-1까지의 합과 n-1Ck까지의 합을 더한 것.
	return binomial(n-1, k-1) + binomial(n-1, k); 

}

int main()
{
	int n, k;
	std::cin >> n >> k;

	std::cout << binomial(n, k);

	return 0;
}