191. 최단 경로

백준

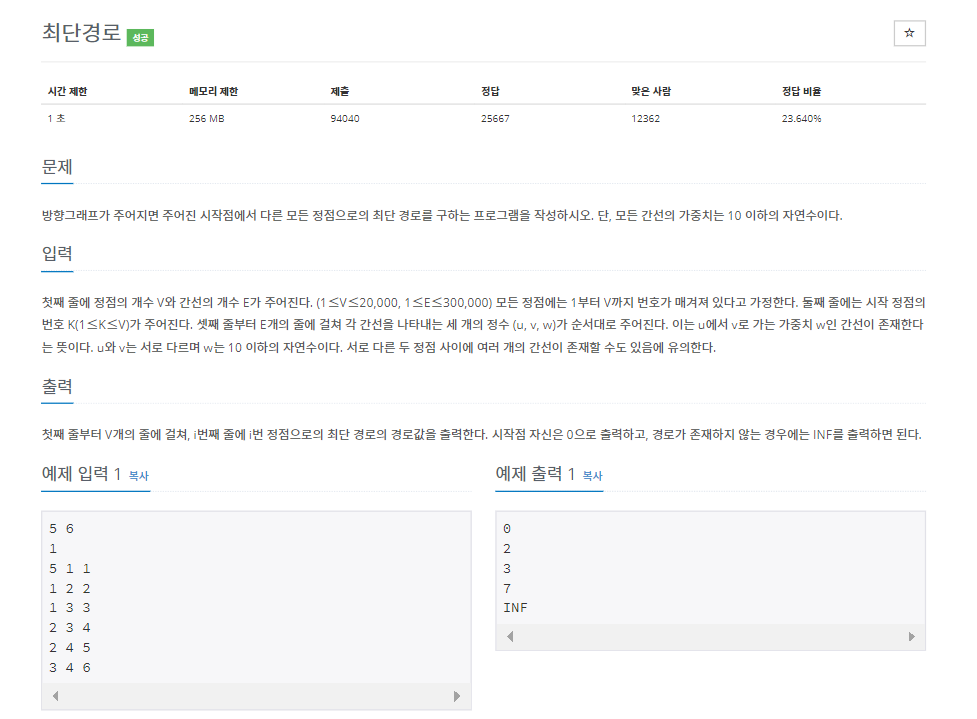
1. 다익스트라 알고리즘

import sys

input = sys.stdlin.readline
INF = int(1e9) #10억 (무한의 의미)

n, m = map(int, input().split())
start = int(input())
graph = [[] for i in range(n + 1)] #1부터 사용하기 위해 +1
visited = [False] * (n + 1) #방문 유무 확인 테이블
distance = [INF] * (n + 1) #최단거리 테이블 

for _ in range(m):
  a, b, c = map(int, input().split())
  graph[a].append((b,c)) #a번 노드에서 b번 노드로 가는 비용이 c

#방문하지 않는 노드 중에서, 가장 최단 거리가 짧은 노드의 번호 반환
def get_smallest_node():
  min_value = INF
  index = 0
  for i in range(1, n + 1):
    if distance[i] < min_value and not visited[i]:
      min_value = distance[i]
      index = i
  return index

def dijkstra(start):
  #시작 노드에 대해서 초기화
  distance[start] = 0
  visited[start] = True
  for j in graph[start]:
    distance[j[0]] = j[1]
  
  #시작 노드를 제외한 전체 n - 1개의 노드에 대해 반복
  for i in range(n - 1):
    #현재 최단 거리가 가장 짧은 노드를 꺼내서, 방문 처리
    now = get_smallest_node()
    visited[now] = True
    #현재 노드와 연결된 다른 노드를 확인
    for j in graph[now]:
      cost = distance[now] + j[1]
      #현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
      if cost < distance[j[0]]:
        distance[j[0]] = cost

dijkstra(start)

for i in range(1, n + 1):
  #도달할 수 없는 경우, 무한(INFINITY)이라고 출력
  if distance[i] == INF:
    print("INFINITY")
  else:
    print(distance[i])

2. C++

#include <bits/stdc++.h>
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정

using namespace std;

// 노드의 개수(N), 간선의 개수(M), 시작 노드 번호(Start)
// 노드의 개수는 최대 100,000개라고 가정
int n, m, start;
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열
vector<pair<int, int> > graph[100001];
// 최단 거리 테이블 만들기
int d[100001];

void dijkstra(int start) {
    priority_queue<pair<int, int> > pq;
    // 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
    pq.push({0, start});
    d[start] = 0;
    while (!pq.empty()) { // 큐가 비어있지 않다면
        // 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
        int dist = -pq.top().first; // 현재 노드까지의 비용 
        int now = pq.top().second; // 현재 노드
        pq.pop();
        // 현재 노드가 이미 처리된 적이 있는 노드라면 무시
        if (d[now] < dist) continue;
        // 현재 노드와 연결된 다른 인접한 노드들을 확인
        for (int i = 0; i < graph[now].size(); i++) {
            int cost = dist + graph[now][i].second;
            // 현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
            if (cost < d[graph[now][i].first]) {
                d[graph[now][i].first] = cost;
                pq.push(make_pair(-cost, graph[now][i].first));
            }
        }
    }
}

int main(void) {
    cin >> n >> m >> start;

    // 모든 간선 정보를 입력받기
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        // a번 노드에서 b번 노드로 가는 비용이 c라는 의미
        graph[a].push_back({b, c});
    }

    // 최단 거리 테이블을 모두 무한으로 초기화
    fill(d, d + 100001, INF);
    
    // 다익스트라 알고리즘을 수행
    dijkstra(start);

    // 모든 노드로 가기 위한 최단 거리를 출력
    for (int i = 1; i <= n; i++) {
        // 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
        if (d[i] == INF) {
            cout << "INF" << '\n';
        }
        // 도달할 수 있는 경우 거리를 출력
        else {
            cout << d[i] << '\n';
        }
    }
}