192. 플로이드

백준

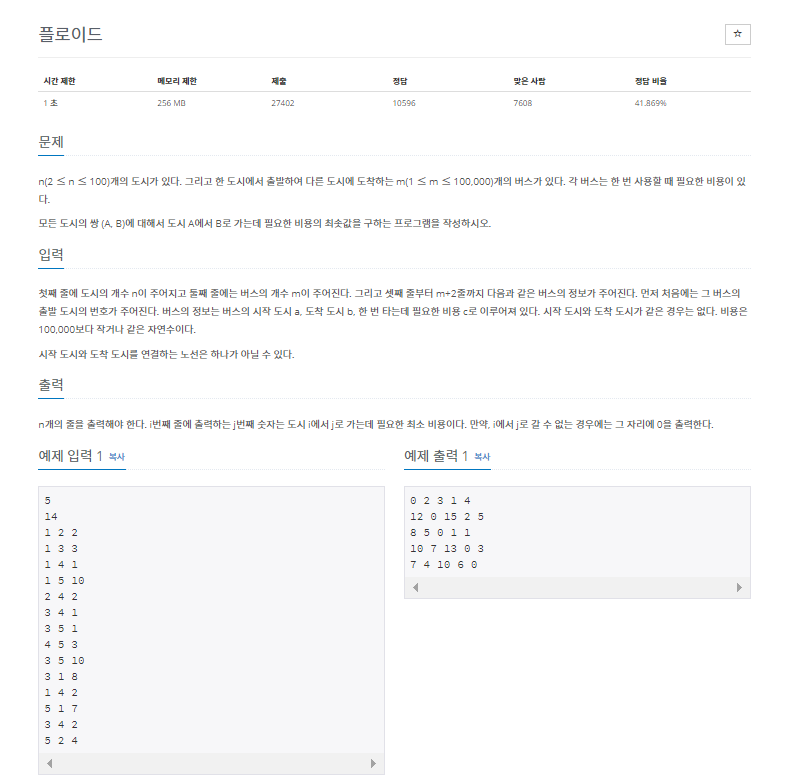
1. 플로이드 워셜 알고리즘

INF = int(1e9)

n = int(input())
m = int(input())

graph = [[INF] * (n + 1) for _ in range(n + 1)]

for a in range(1, n + 1):
  for b in range(1, n + 1):
    if a == b:
      graph[a][b] = 0

for _ in range(m):
  a, b, c = map(int, input().split())
  graph[a][b] = min(c, graph[a][b])

for k in range(1, n + 1):
  for a in range(1, n + 1):
    for b in range(1, n + 1):
      graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

for a in range(1, n + 1):
  for b in range(1, n + 1):
    if graph[a][b] == INF:
      print(0, end=" ")
    else:
      print(graph[a][b], end=" ")

  print()

2. C++

#include <bits/stdc++.h>
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정

using namespace std;

// 노드의 개수(N), 간선의 개수(M)
// 노드의 개수는 최대 500개라고 가정
int n, m;
// 2차원 배열(그래프 표현)를 만들기
int graph[501][501];

int main(void) {
    cin >> n >> m;

    // 최단 거리 테이블을 모두 무한으로 초기화
    for (int i = 0; i < 501; i++) {
        fill(graph[i], graph[i] + 501, INF);
    }

    // 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
    for (int a = 1; a <= n; a++) {
        for (int b = 1; b <= n; b++) {
            if (a == b) graph[a][b] = 0;
        }
    }

    // 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
    for (int i = 0; i < m; i++) {
        // A에서 B로 가는 비용은 C라고 설정
        int a, b, c;
        cin >> a >> b >> c;
        graph[a][b] = min(c, graph[a][b]);
    }
    
    // 점화식에 따라 플로이드 워셜 알고리즘을 수행
    for (int k = 1; k <= n; k++) {
        for (int a = 1; a <= n; a++) {
            for (int b = 1; b <= n; b++) {
                graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b]);
            }
        }
    }

    // 수행된 결과를 출력
    for (int a = 1; a <= n; a++) {
        for (int b = 1; b <= n; b++) {
            // 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
            if (graph[a][b] == INF) {
                cout << 0 << ' ';
            }
            // 도달할 수 있는 경우 거리를 출력
            else {
                cout << graph[a][b] << ' ';
            }
        }
        cout << '\n';
    }
}