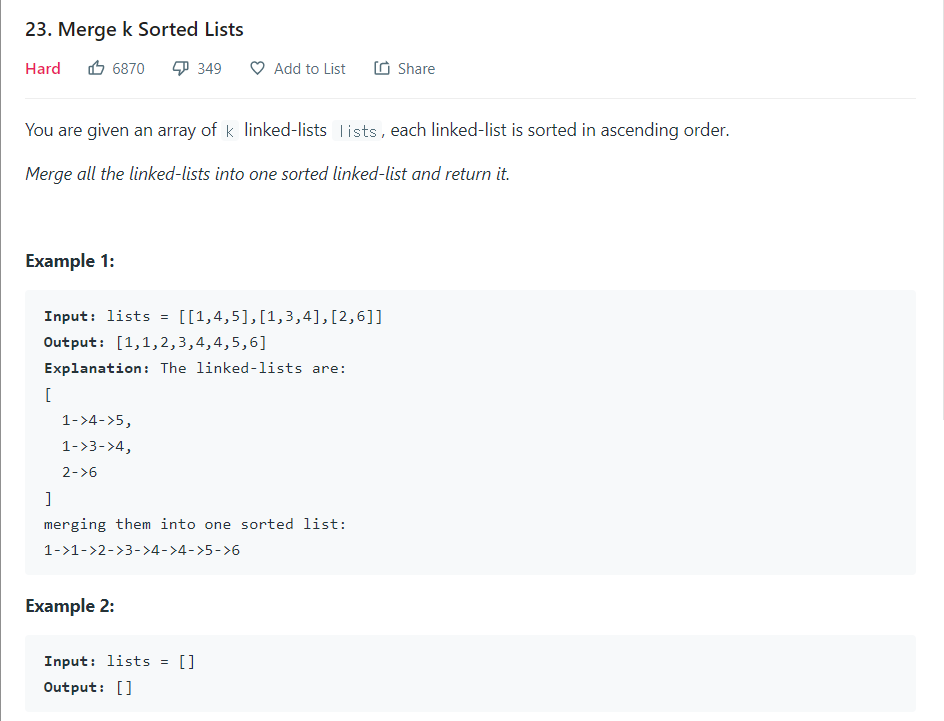
- k개의 정렬된 리스트를 1개의 정렬된 리스트로 병합하라.
1. 우선순위 큐를 이용한 리스트 병합
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
root = result = ListNode(None)
heap = []
#각 연결 리스트의 루트를 힙에 저장
for i in range(len(lists)):
if lists[i]:
heapq.heappush(heap, (lists[i].val, i, lists[i]))
#힙 추출 이후 다음 노드는 다시 저장
while heap:
node = heapq.heappop(heap)
idx = node[1]
result.next = node[2]
result = result.next
if result.next:
heapq.heappush(heap, (result.next.val, idx, result.next))
return root.next
-
이 문제의 난이도는 '어려움'으로 표기되어 있지만 사실 이 문제는 우선순위 큐를 사용하면 매우 쉽게 풀이할 수 있다.
-
대부분의 우선순위 큐 풀이에 거의 항상 heapq 모듈을 사용하므로 잘 파악해두자.
-
lists는 3개의 연결 리스트인 [[1, 4, 5],[1, 3, 4],[2, 6]]로 구성된 입력값이며, 이 코드는 각 연결 리스트의 루트를 힙에 저장하게 된다.
-
heapq 모듈은 최소 힙(Min Heap)을 지원하며, 따라서 lst.val이 작은 순서대로 pop()할 수 있다.
- 이렇게 저장하면 TypeError:'<' not supported between instances of 'ListNode' and 'ListNode'라는 에러가 발생하는데 이 에러 메세지는 직관적이지 않아 파악하기가 쉽지 않지만 '중복된 값을 넣을 수 없다'라는 뜻이다.
-
이 문제 예시의 입력값은 3개의 연결 리스트 중 첫 번째와 두 번째의 루트가 각각 1로 동일하다. 이렇게 동일한 값은 heappush() 함수에서 에러를 발생하기 때문에 중복된 값을 구분할 수 있는 추가 인자가 필요하다.
- 오로지 에러를 방지하기 위한 용도로 연결 리스트의 순서를 적절히 삽입해 보자
-
이제 heappop() 으로 값을 추출하면 가장 작은 노드의 연결 리스트부터 차례대로 나오게 되며, 이 값을 결과가 될 노드 result에 하나씩 추가한다.
-
k개의 연결 리스트가 모두 힙에 계속 들어 있어야 그 중에서 가장 작은 노드가 항상 차례대로 나올 수 있으므로, 추출한 연결 리스트의 그 다음 노드는 다시 힙에 추가한다.
-
힙에 아무 값도 남지 않을 때까지 반복하면 result에는 작은 노드부터 차례대로 연결된다.
-
✔ 우선순위 큐
-
우선순위 큐
- 큐 또는 스택과 같은 추상 자료형과 유사하지만 추가로 각 요소의 '우선순위'와 연관되어 있다.
-
우선순위 큐는 어떠한 특정 조건에 따라 우선순위가 가장 높은 요소가 추출되는 자료형이다.
- 대표적으로는 최댓값 추출을 들 수 있는데, 예를 들어 큐에 [1, 4, 5, 3, 2]가 들어 있고, 최댓값을 추출하는 우선순위 큐가 있다고 가정하면, 이 경우 항상 남아 있는 요소들의 최댓값이 우선순위에 따라 추출되어 5, 4, 3, 2, 1 순으로 추출된다.
-
정렬 알고리즘을 사용하면 우선운위 큐를 만들 수 있다는 의미이기도 하다.
-
n개의 요소를 정렬하는 데 S(n)의 시간이 든다고 할 때, 새 요소를 삽입하거나 요소를 삭제하는데는 O(S(n))의 시간이 걸린다.
-
반면, 내림차순으로 정렬했을 때 최댓값을 가져오는 데는 맨 앞의 값을 가져오기만 하면 되므로 O(1)로 가능하다.
-
대개 정렬에는 O(nlogn)이 필요하기 때문에 O(S(n))은 O(nlogn) 정도가 든다.
그러나, 실제로는 이처럼 단순 정렬보다는 힙 정렬 등의좀 더 효율적인 방법을 사용한다.
-
-
이외에도 최단 경로를 탐색하는 다익스트라(Dijikstra) 알고리즘 등 우선순위 큐는 다양한 분야에 활용되며, 힙(Heap) 자료구조와도 관련이 깊다.
