34. Permutations

리트코드

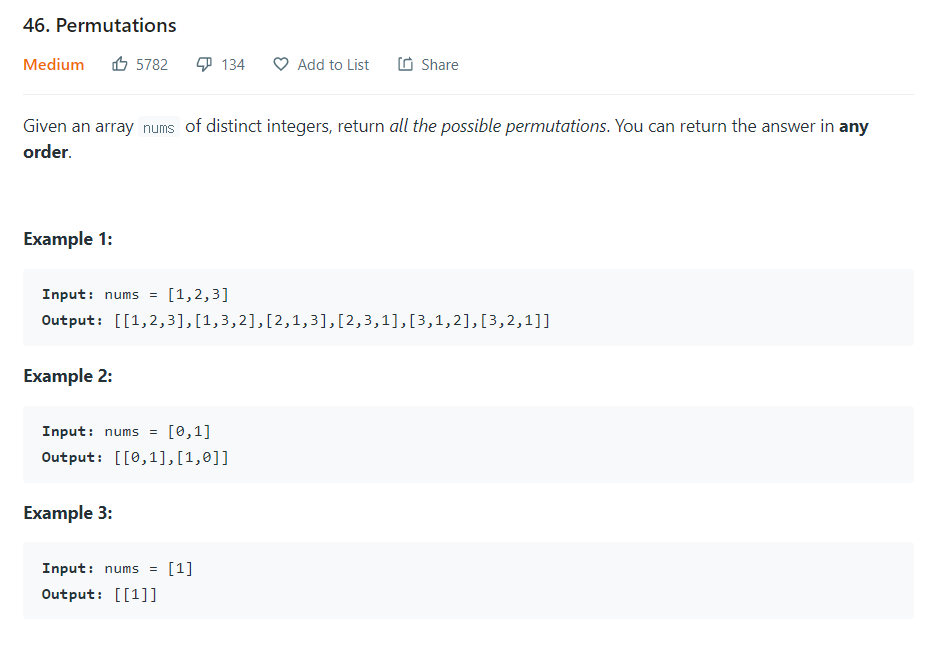
• 서로 다른 정수를 입력받아 가능한 모든 순열을 리턴하라.

  • 순열의 수 추출(경우의 수) : nPr = n!/(n-r)!

1. DFS를 활용한 순열 생성 (40ms)

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        results = []
        prev_elements = []
        
        def dfs(elements):
            
            #리프 노드일 때 결과 추가
            if len(elements) == 0:
                results.append(prev_elements[:])
            
            #순열 생성 재귀 호출 
            for e in elements:
                next_elements = elements[:]
                next_elements.remove(e)
                
                prev_elements.append(e)
                dfs(next_elements)
                prev_elements.pop()
                
        dfs(nums)
        return results
        

• 이 문제는 모든 결과를 생성해내야 하는데 생성하는 문제일 때, 경우의 수만 계산하는 것에 비해서는 다소 까다로운 편이다.

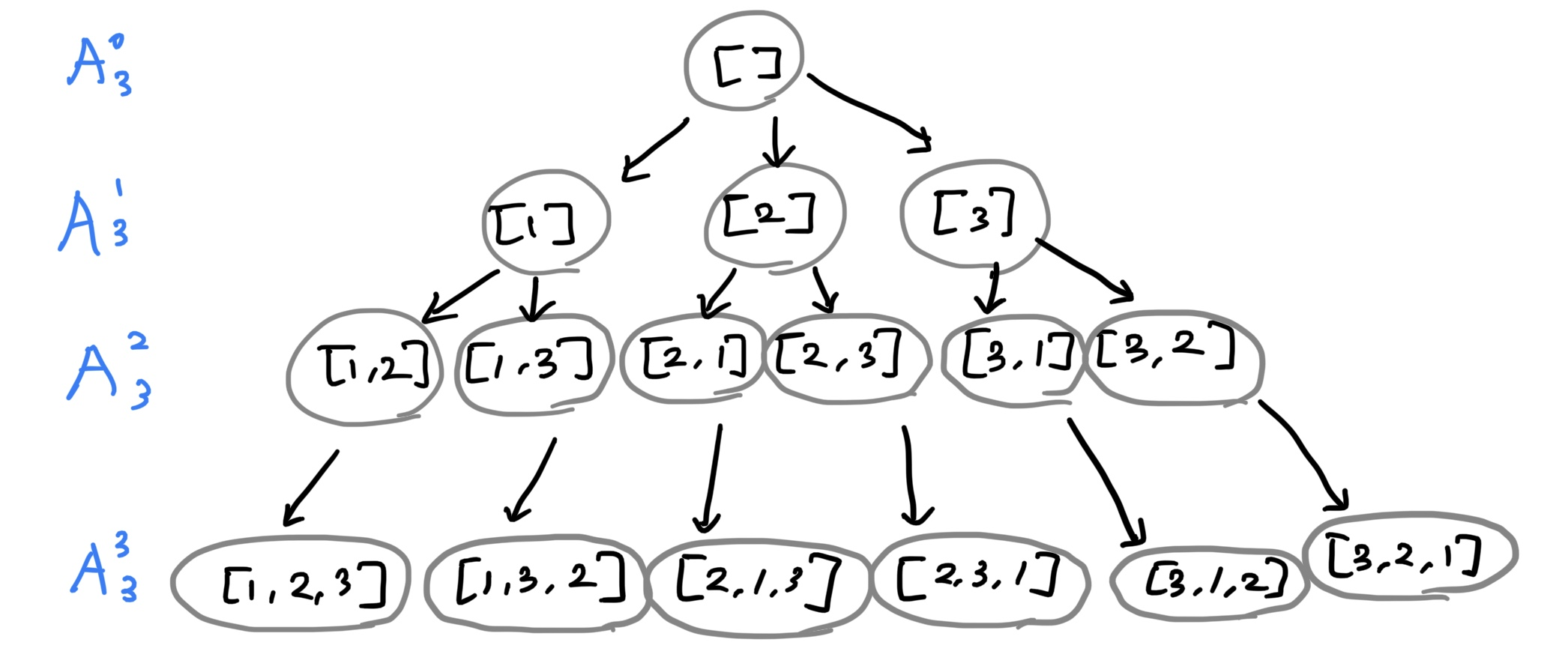
  • 순열이란 결국 모든 가능한 경우를 그래프 형태로 나열한 결과라고 할 수 있기 때문에 그래프로 표현해보면 다음과 같다.

    

  • 이 그림에서 리프(Leaf) 노드, 즉 마지막 A(3,3)의 모든 모드가 순열의 최종 결과이다.

  • 레벨이 증가할수록 자식 노드의 개수는 점점 작아진다.

    • A(0,3)의 자식 노드는 3개였다가 A(1,3)의 자식 노드는 2개, A(2,3)의 자식 노드는 1개 순으로, 이는 순열의 수식이기도 한 3 x 2 x 1 형태이기도 하다.

    • 만약 자식 노드의 개수도 마찬가지로 5개부터 4개, 3개, ... , 1개 순이 될 것이다.

  
  

• dfs( ) 탐색 함수를 만들어보자.

  • 이전 값을 하나씩 덧붙여 계속 재귀 호출을 진행하다 리프 노드에 도달한 경우, 즉 len(elements) == 0일 때 결과를 하나씩 담는다.

  • 중요한 부분은 결과를 추가할 때 prev_elements[:]로 처리해야한다는 점이다.

    • 파이썬은 모든 객체를 참조하는 형태로 처리되므로 만약 results.append(prev_elements)를 하게 되면 결과 값이 추가되는 게 아닌 prev_elements에 대한 참조가 추가되며, 이 경우 참조된 값이 변경될 경우 같이 바뀌게 된다.

    • 따라서 반드시 값을 복사하는 형태로 참조 관계를 갖지 않도록 처리해야 한다.

    • copy() 혹은 deepcopy()를 사용할 수 있다.

  

  
  
  

2. itertools 모듈 사용 (36ms)

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        return list(map(list, itertools.permutations(nums)))

• itertools 모듈

  • 반복자 생성에 최적화된 효율적인 기능들을 제공하므로, 실무에서는 알고리즘으로 직접 구현하기 보다는 가능하다면 itertools 모듈을 사용하는 편이 낫다.

    • 이미 잘 구현된 라이브러리라 직접 구현함에 따른 버그 발생 가능성이 낮고, 무엇보다 효율적으로 설계된 C 라이브러리라 속도에도 이점이 있다.

• 딱 한가지 걸리는 부분은, 이 함수의 결과가 리스트 내 튜플(Tuple)이라는 점이다.

  • permutations( )함수가 튜플 모음을 반환하기 때문이다.

   
   class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        return list(itertools.permutations(nums))

   
   

• 리트코드에서는 리스트를 반환하도록 요구하기 때문에 코드를 다음과 같이 변환해야한다.