35. Combinations

리트코드

• 전체 수 n을 입력받아 k개의 조합(Combination)을 리턴하라.

  • nCr = n! / r! (n-r)!

1. DFS로 k개 조합 생성 (536ms)

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        results = []
        
        def dfs(elements, start:int, k:int):
            if k == 0:
                results.append(elements[:])
                
            #자기 이전의 모든 값을 고정하여 재귀 호출
            for i in range(start, n + 1):
                elements.append(i)
                dfs(elements, i+1, k-1)
                elements.pop()
                
        dfs([], 1, k)
        return results

• 이 문제의 경우 입력값이 너무 단순하므로 1을 더 늘려보자.

  • 즉 n=5, k=3일 때, 5! / 3!(5-3)! = 10이다.

  • 10가지 경우를 모두 나열해보면 다음과 같다.

  

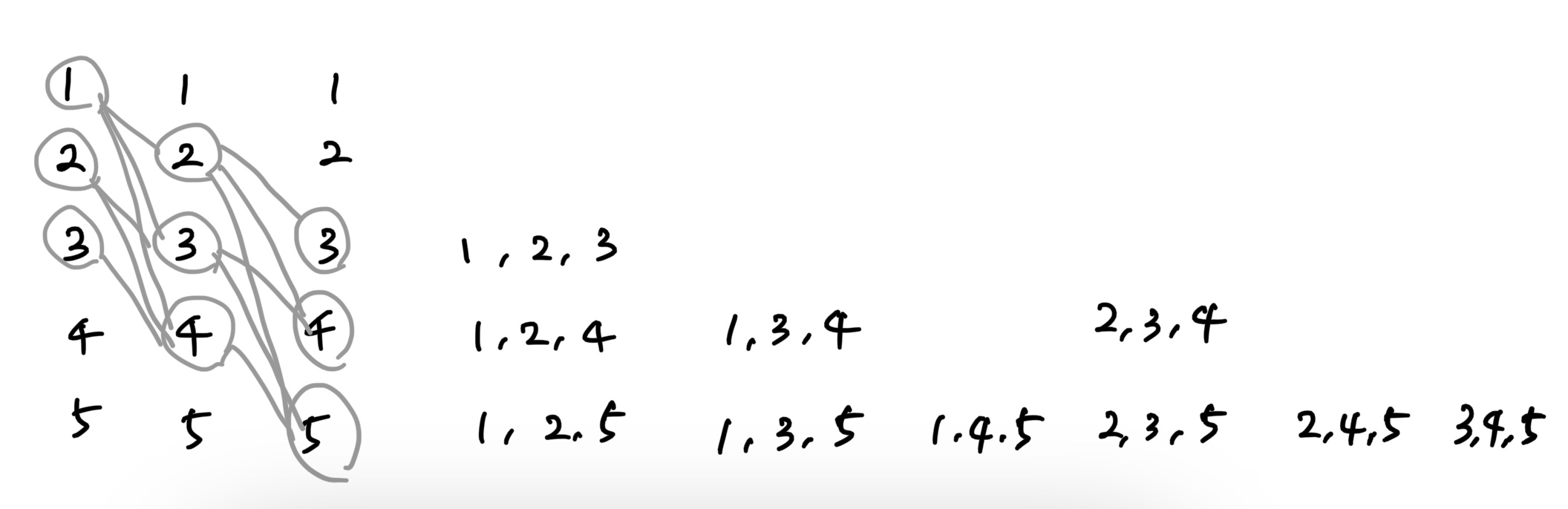
• 순열의 경우 자기 자신을 제외하고 모든 요소를 next_elements로 처리했으나, 이와달리 조합의 경우 자기 자신뿐만 아니라 앞의 모든 요소를 배제하고 next_elements를 구성한다.

  • 따라서 여기서는 그냥 elements라는 이름으로 처리한다.
  
  

• dfs( ) 함수

  • 여기서는 1부터 순서대로 for 문으로 반복하되, 재귀 호출할 때 넘겨주는 값은 자기 자신의 이전의 모든 값을 고정하여 넘긴다.

  • 따라서 남아 있는 값끼리 나머지 조합을 수행하게 되며, k=0이 되면 결과에 삽입한다.

  • 참조로 처리되지 않도록, 결과는 [:]연산자로 값 자체를 복사해 추가한다.

➕

34번 순열 문제와 이 문제는 서로 비슷한 면이 있지만, 순열과 조합이 다르듯 구현방식에도 차이가 있다.

무엇보다 이 문제는 모든 순열을 생성하는 34번 문제와 달리, k개의 조합만을 생성해야 한다는 제약 조건이 추가된 문제다.

따라서 dfs( )함수에서 k값을 별도로 전달받아 1씩 줄여나가며 재귀호출하는 구조로,
k가 0이 되면 바로 빠져나가는 로직이 추가되어 있다.

2. itertools 모듈 사용 (76ms)

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        return list(itertools.combinations(range(1, n+1), k))
        

• 순열 문제에서 itertools.permutations( )가 있었던 것 처럼 itertools.combinations( )도 당연히 지원한다.