36. Combination Sum

리트코드

• 숫자 집합 candidates를 조합하여 합이 target이 되는 원소를 나열하라.

  • 각 원소는 중복으로 나열 가능하다.

1. DFS로 중복 조합 그래프 탐색

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        result = []
        
        def dfs(csum, index, path):
            #종료조건
            
            if csum < 0:
                return
            
            if csum == 0:
                result.append(path)
                return
            
            #자신부터 하위 원소 까지의 나열 재귀 호출
            
            for i in range(index, len(candidates)):
                dfs(csum - candidates[i], i, path + [candidates[i]])
                
        
        dfs(target, 0, [])
        return result

• 합 tartget을 만들 수 있는 모든 번호 조합을 찾는 문제이다.

• 입력값의 중복 조합 그래프를 풀이하는 문제로 도식화 할 수 있다.

  

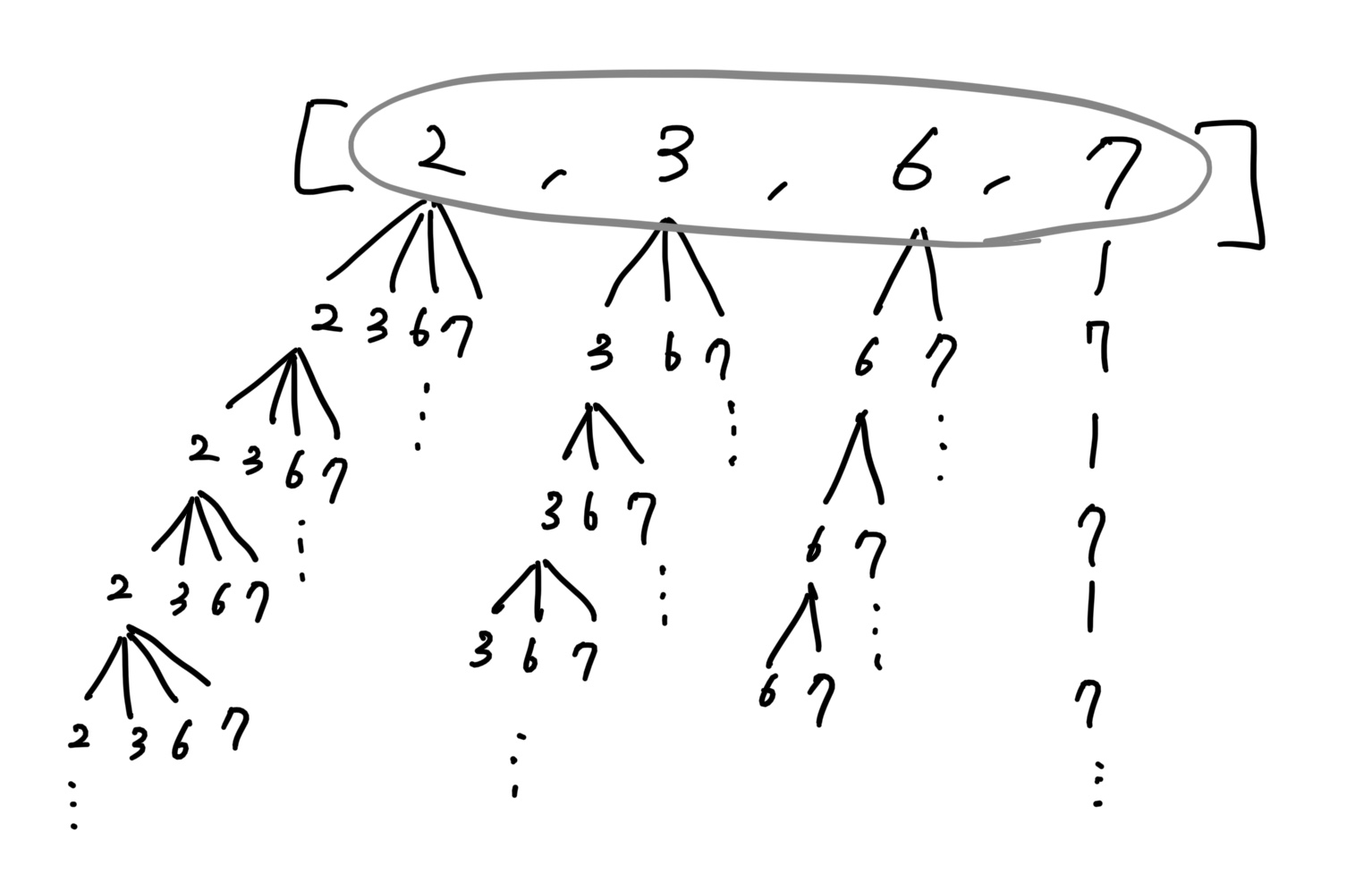
  • 모든 중복 조합에서 찾아야 하기 때문에, 이 그림과 같이 항상 부모의 값부터 시작하는 그래프로 구성할 수 있다.

• 이제 이 중복 조합 그래프를 DFS로 탐색할 수 있다.

  • DFS로 재귀 호출하되, dfs( )함수의

    • 첫 번째 파라미터는 합을 갱신해나갈 csum(candidates_sum이라는 의미),

    • 두 번째 파라미터는 순서(자기 자신을 포함),

    • 세 번째 파라미터는 지금까지의 탐색 경로로 정한다.

• 그러나, 이 탐색코드는 종료 조건이 없으며, 자기 자신을 포함하기 때문에 무한히 탐색하게 될 것이다.

  • 종료 조건은 다음 2가지로 정한다.

    1) csum < 0 (마이너스인 경우): 목표값을 초과한 경우로 탐색을 종료한다.

    2) csum = 0 (0인 경우): csum의 초기값은 targe이며, 따라서 csum의 0은 target과 일치하는 정답이므로 결과 리스트에 추가하고 탐색을 종료한다.

  
  

• 만약 입력값에 0이 포함되어 있다면 어떻게 될까? 종료 조건을 만족할 수 없기 때문에 무한히 깊이 탐색을 시도하게 된다.

  • 실제로는 입력값 0에 대한 예외 처리도 필요하다.
    (리트코드의 테스트 케이스에는 0이 포함되지 않는다.)

• 이 문제를 순열로 풀이하기 위해서는 완성된 전체 코드에서 dfs( )를 호출하는 곳에서 다음과 같이 i가 아닌 0을 기입하면 된다.

  그렇게 하면 항상 첫 번째 값부터 탐색을 시도하기 때문에 순열로 풀이할 수 있을 것이다.

	dfs(csum - cadidates[i], 0, path + [candidates[i]])