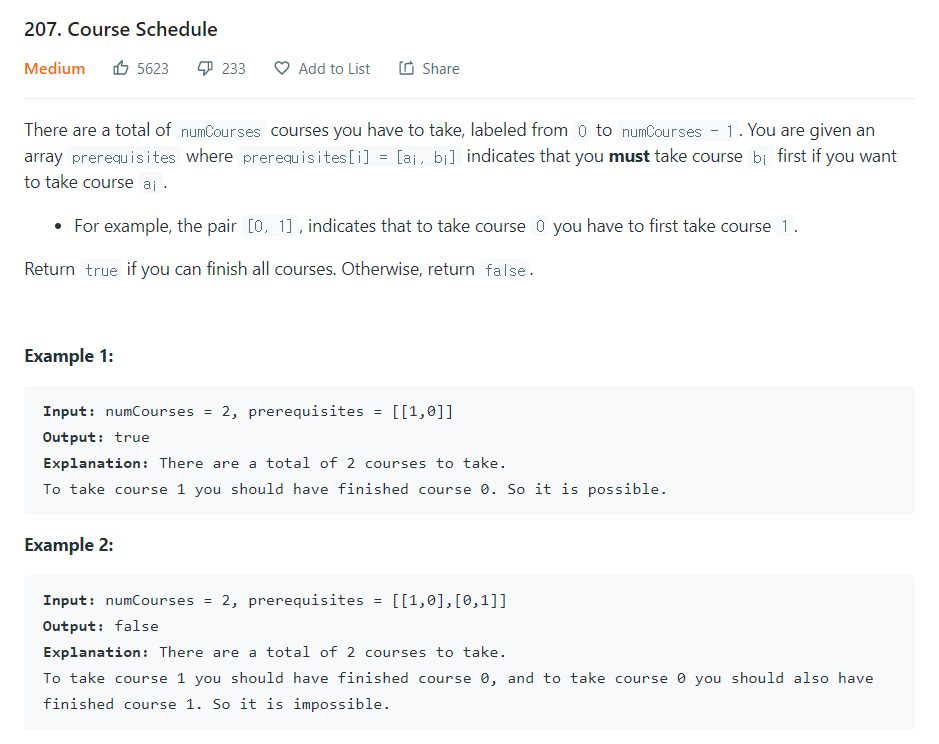
- 0을 완료하기 위해서는 1을 끝내야 한다는 것을 [0,1] 쌍으로 표현하는 n개의 코스가 있다.
코스 개수 n과 이 쌍들을 입력으로 받았을 때 모든 코스가 완료 가능한지 판별하라.

1. DFS로 순환 구조 판별 (920ms)
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
graph = collections.defaultdict(list)
#그래프 구성
for x, y in prerequisites:
graph[x].append(y)
traced = set()
def dfs(i):
#순환 구조이면 False
if i in traced:
return False
traced.add(i)
for y in graph[i]:
if not dfs(y):
return False
#탐색 종료 후 순환 노드 삭제
traced.remove(i)
return True
#순환 구조 판별
for x in list(graph):
if not dfs(x):
return False
return True
-
이 문제는 그래프가 순환(Cyclic) 구조인지를 판별하는 문제로 풀이할 수 있다.
- 순환 구조라면 계속 뱅글뱅글 맴돌게 될 것이고, 해당 코스는 처리할 수 없기 때문이다.
-
먼저 여기서는 페어들의 목록인 prerequsites 변수를 풀어서 그래프로 표현한다.
-
페어의 첫 번째 값을 x, 두 번째 값을 y로 하되 y는 복수 개로 구성할 수 있게 한다.
-
이렇게 하면 'x':['y1', 'y2'] 같은 구조가 될 것이다.
-
-
순환 구조를 판별하기 위해 앞서 이미 방문했던 노드를 traced 변수에 저장한다.
-
이미 방문했던 곳을 중복 방문하게 된다면 순환 구조로 간주할 수 있고, 이 경우 False를 리턴하고 종료할 수 있다.
-
traced는 중복 값을 갖지 않으므로 set() 집합 자료형으로 정한다.
-
-
순환 구조를 찾기 위한 탐색은 DFS로 진행한다.
-
여기서 DFS 함수인
dfs()에서는 현재 노드가 이미 방문했던 노드 집합인 traced에 존재한다면 순환 구조이므로 False를 리턴한다.-
False는 계속 상위로 리턴되어 최종 결과도 False를 리턴하게 될 것이다.
-
탐색은 재귀로 진행하되, 해당 노드를 이용한 모든 탐색이 끝나게 된다면
traced.remove(i)로 방문했던 내역을 반드시 삭제해야 한다. -
그렇지 않으면 형제 노드가 방문한 노드까지 남게 되어, 자식 노드 입장에서는 순환이 아닌데 순환이라고 잘못 판단할 수 있기 때문이다.
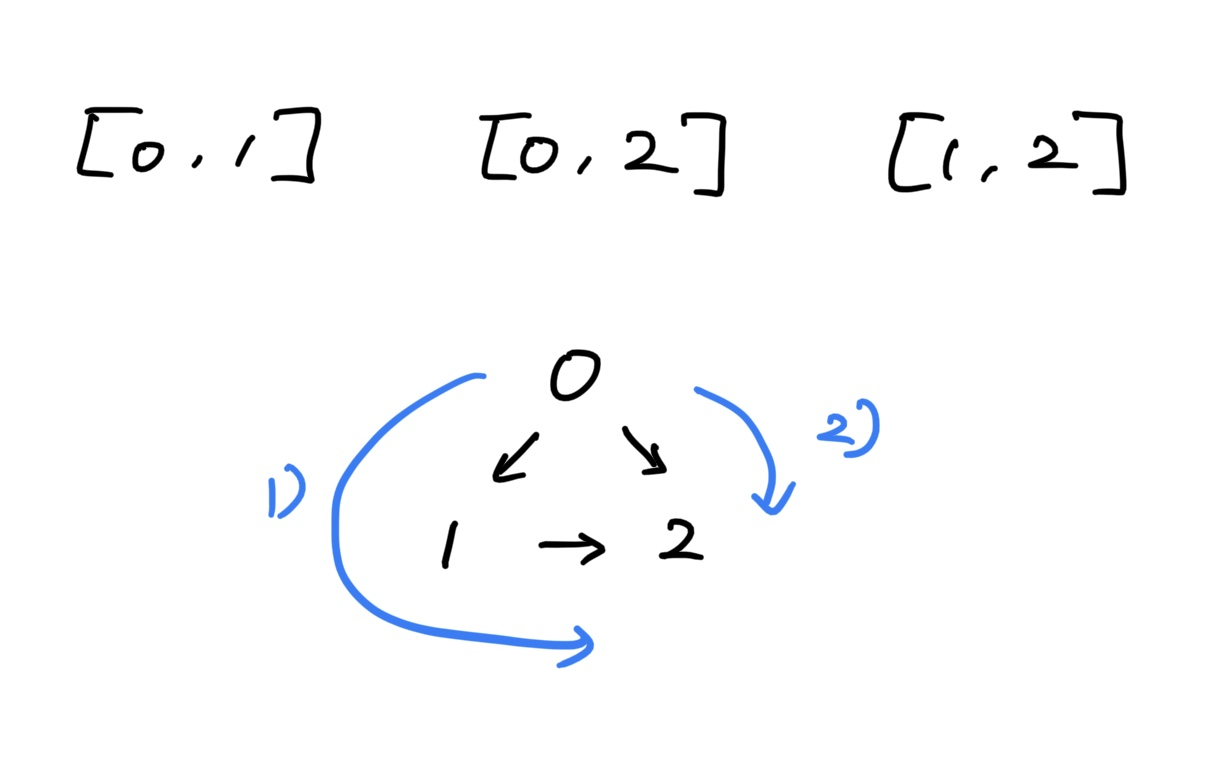
-
여기서는 입력값이 [[0,1], [0,2], [1,2]]일 때, 이 그래프는 순환이 존재하지 않으므로 결과는 True가 되어야 한다.
-
만약 이미 방문한 노드를 삭제하지 않고 그대로 둔다면 1)번 경로로 탐색할 때 방문했던 노드들이 그대로 남게 될 것이고 ([0, 1, 2]), 2)번 경로로 탐색할 때 2 노드가 이미 방문했던 노드라고 잘못 판단할 것이다.
-
1)번 경로와 2)번 경로는 형제 노드 간의 탐색이기 때문에 서로 관련성이 없어야 하므로 1)번 경로로 탐색이 끝난 이후에는
traced.remove(i)로 1, 2 노드가 모두 삭제되어야 한다.
-
-
2. 가지치기를 이용한 최적화 (96ms)
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
graph = collections.defaultdict(list)
#그래프 구성
for x, y in prerequisites:
graph[x].append(y)
traced = set()
visited = set()
def dfs(i):
#순환 구조이면 False
if i in traced:
return False
#이미 방문했던 노드이면 False
if i in visited:
return True
traced.add(i)
for y in graph[i]:
if not dfs(y):
return False
#탐색 종료 후 순환 노드 삭제
traced.remove(i)
#탐색 종료 후 방문 노드 추가
visited.add(i)
return True
return True
#순환 구조 판별
for x in list(graph):
if not dfs(x):
return False
return True
-
DFS 풀이는 순환이 발견될 때까지 모든 자식 노드를 탐색하는 구조로 되어 있다.
-
이는 서로 복잡하게 호출하는 구조로 되어 있다면, 불필요하게 동일한 그래프를 여러 번 탐색하게 될 수도 있다.
-
따라서, 한 번 방문했던 그래프는 두 번 이상 방문하지 않도록 무조건 True로 리턴하는 구조로 개선한다면, 탐색시간을 획기적으로 줄일 수 있을 것이다.
-
그리고 원래 DFS는 가지치기 하도록 구현하는 게 올바른 구현 방법이다.
-
➕ defaultdict 순회 문제
for x in list(graph):
...- graph 변수 앞에
list()로 감쌌는데, 이는 RuntimeError: dictionary changed size during iteration 에러가 발생했기 때문이다.
-
collections 모듈의 defaultdict를 사용해 키가 없는 딕셔너리에 대해서 빈 값 조회시 널(Null) 오류가 발생하지 않도록 처리한 바 있는데, 문제는 여기에 있다.
- 여기서 사용한 defaultdict가 존재하지 않는 키를 조회할 때 오류를 내지 않기 위해 항상 디폴트를 생성하는 구조로 되어 있다는 점이다.
-
해당 반복문이 제대로 실행되려면 graph 변수를
defaultdict()에서 분리해서 고정시킬 필요가 있다. -
list()로 묶어서 해결하라는 답변을 스택 오버플로에서 찾을 수 있다.-
즉, 새로운 복사본을 만들라는 얘기다.
-
graph를
list()로 묶을 경우 새로운 복사본이 생성되면서 다른 ID를 갖게 된다.
-
이런 문제는 좀처럼 해결책을 찾기가 쉽지 않다. 무엇보다 문제를 해결하는 데 많은 시간이 소모되기 때문에, 시간 제한이 있는 온라인 코딩 테스트에서 이런 문제를 맞닥뜨리면 매우 당황하게 된다.
이 같은 에러는 알고리즘과도 전혀 관련이 없는, 언어와 컴파일러의 특징에 가까운 에러이기 때문에 여기서 시간을 많이 소모하게 되면 억울할 정도로 많이 손해를 볼 수 있다.
적어도 파이썬으로 풀이하기로 마음먹었다면, 파이썬의 버전별 특징과 파이썬의 공식 인터프리터인 CPython의 동작 원리에 대해 충분히 익혀둬야 한다.
