43. Diameter of Binary Tree

아현·2021년 4월 23일

Algorithm

목록 보기

44/400

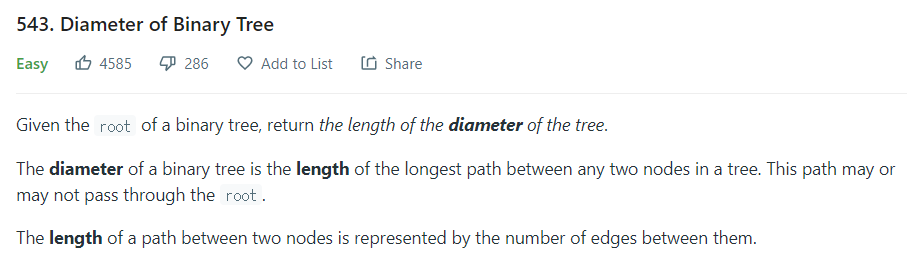
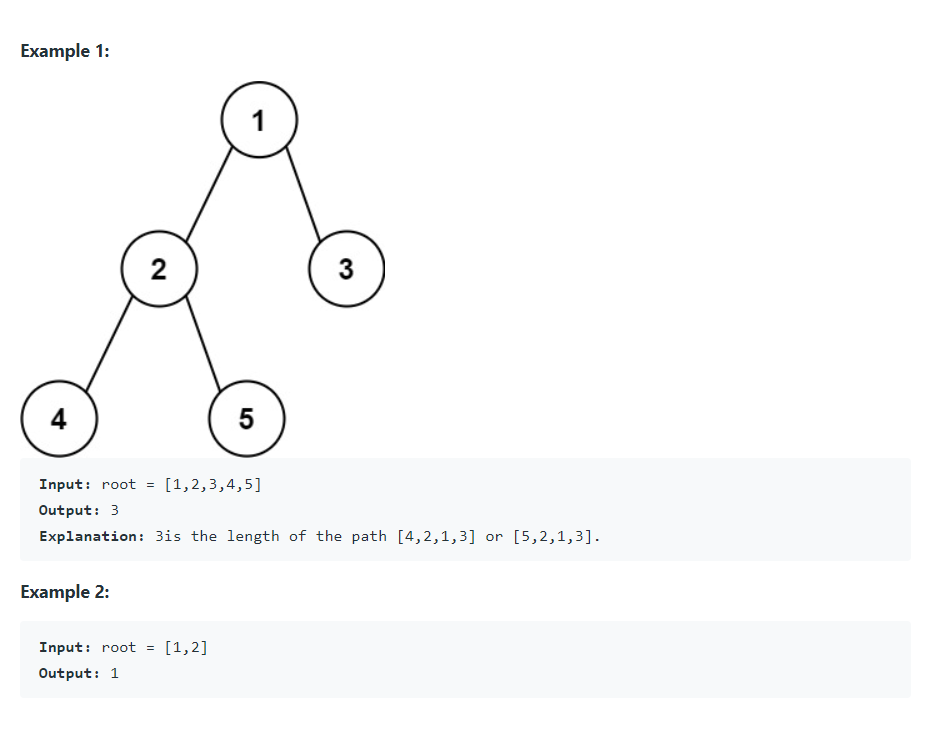
이진 트리에서 두 노드 간 가장 긴 경로의 길이를 출력하라

1. 상태값 누적 트리 DFS


# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    longest: int = 0
    def diameterOfBinaryTree(self, root: TreeNode) -> int:
        def dfs(node: TreeNode) -> int:
            if not node:
                return -1
            
            #왼쪽, 오른쪽이 각 리프 노드까지 탐색
            left = dfs(node.left)
            right = dfs(node.right)
            
            #가장 긴 경로
            self.longest = max(self.longest, left + right + 2)
            
            #상태값
            return max(left, right) + 1
        
        dfs(root)
        return self.longest

가장 긴 경로를 찾는 방법은 먼저 가장 말단, 즉 리프 노드까지 탐색한 다음 부모로 거슬러 올라가면서 각각의 거리를 계산해 상태값을 업데이트하면서 다음과 같이 누적해 나가면 될 것 같다.

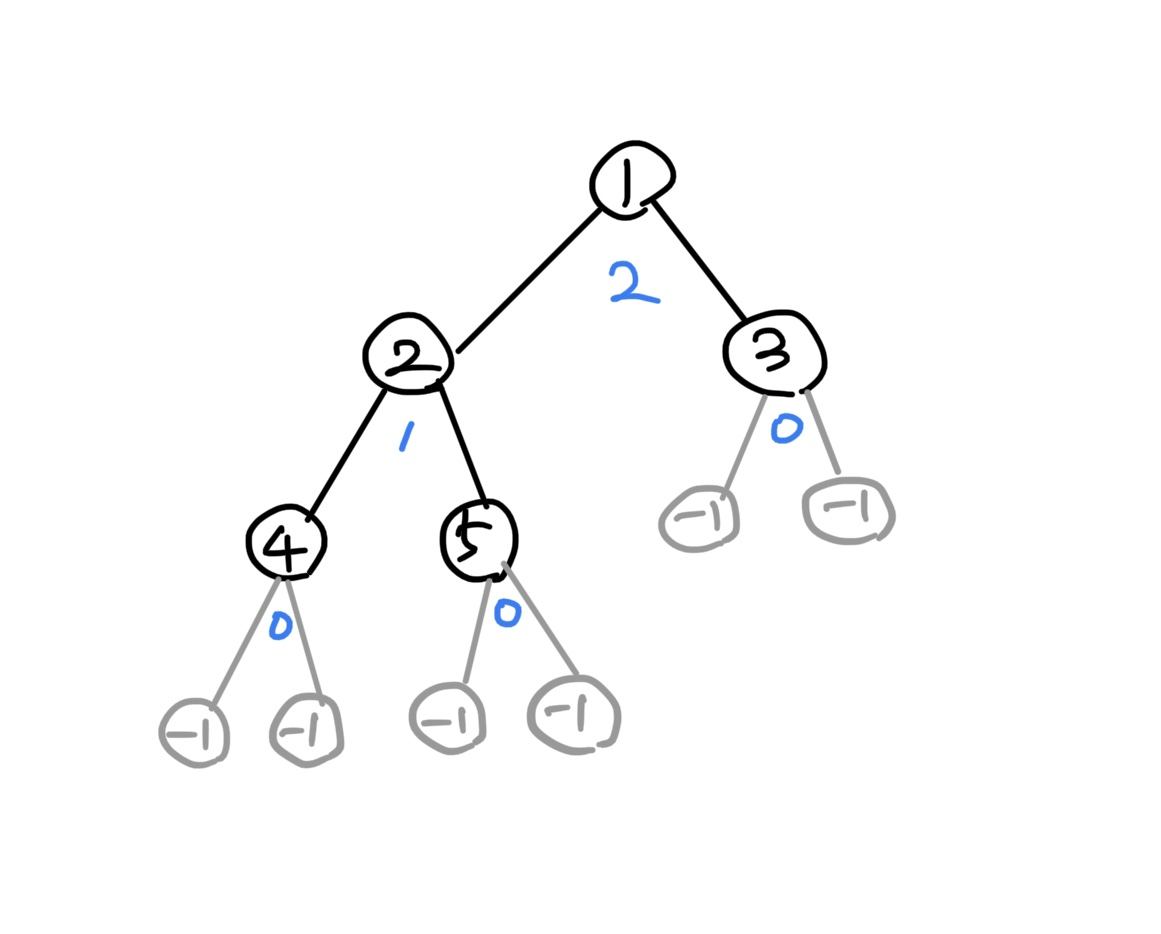
<트리의 가장 말단, 리프 노드에서 부모까지 상태값 누적 트리>

존재하지 않는 노드에도 -1이라는 값을 부여한다.
- 정 이진 트리 (Full Binary Tree)가 아닌 대부분의 경우에는 존재하지 않는 자식 노드에 -1을 부여해 페널티를 주기 위함이다.
이렇게 거슬러 올라가 최종 루트에서 상태값은 2, 거리는 3이 된다.
- 상태값은 리프노드에서 현재 노드까지의 거리다.
- 거리는 왼쪽 자식 노드의 상태값과 오른쪽 자식 노드의 상태값의 합에 2를 더한 값이다.
- 최종적으로 거리는 왼쪽 자식 노드의 리프노드에서 현재 노드까지의 거리(상태값)와, 오른쪽 자식 노드의 리프 노드에서 현재 노드까지의 거리(상태값)의 합에 2(현재 노드와 왼쪽, 오른쪽 자식 노드와의 거리)를 더한 것이다.

먼저 탐색함수부터 살펴본다.
- 계속 재귀 호출을 통해 왼쪽, 오른쪽의 각 리프 노드까지 DFS로 탐색한다.
- 이후 2개의 값을 계산하는데, 하나는 최종 결과가 될 가장 긴 경로 self.longest
  나머지 하나는 앞서 얘기한 상태값 max(left, right) + 1을 말한다.
자식 노드가 하나도 없는 경우 left, right는 모두 -1이고, 이 경우 거리는 0, 상태값도 0이 된다.
자식 노드가 모두 존재하는 경우에는, 그리고 자식 노드가 둘 다 상태값이 0이라면, 거리인 a는 2, 상태값인 b는 1이 된다.
- 즉, 거리는 왼쪽, 오른쪽 자식 사이의 경로이므로 2를 더하게 되고, 상태값은 양쪽 자식 중 최대 상태값과 부모까지의 거리인 1을 더하게 된다.
- 위의 그림에서도 루트의 상태값은 2, 거리값은 3이된다.
  - 정답은 거리값인 3이다.

➕ 중첩 함수에서 클래스 변수를 사용한 이유

중첩함수 (Nested Function)를 사용할 때, 왜 longest 변수를 함수 내에서 선언하지 않고 바깥에 클래스 변수로 선언해서 번거롭게 self.longest 형태로 사용했을까?

중첩 함수는 부모 함수의 변수를 자유롭게 읽어들일 수 있다.
그러나, 중첩 함수에서 부모 함수의 변수를 재할당하게 되면 참조 ID가 변경되며 별도의 로컬 변수로 선언된다.
- self.longest = max(self.longest, left + right + 2)라는 부분이 있다.
- longest 변수에 값을 재 할당하는 부분인데 여기서는 self.longest를 사용했다.
- 왜냐면 재할당을 해야 하기 때문이다. 따라서 부모 함수의 변수를 그대로 사용할 수 없었고, 함수 바깥에서 클래스 변수로 선언한 후 사용했다.

만약, longest의 값이 숫자나 문자가 아니라 리스트나 딕셔너리 같은 자료형이라면 append() 등의 메소드를 이용해 재할당 없이 조작이 가능하다.

그러나, 숫자나 문자인 경우 불변 객체이기 때문에 중첩 함수 내에서는 값을 변경할 수 없다. 이 때문에 클래스 변수를 사용했다.