44. Longest Univalue Path

리트코드

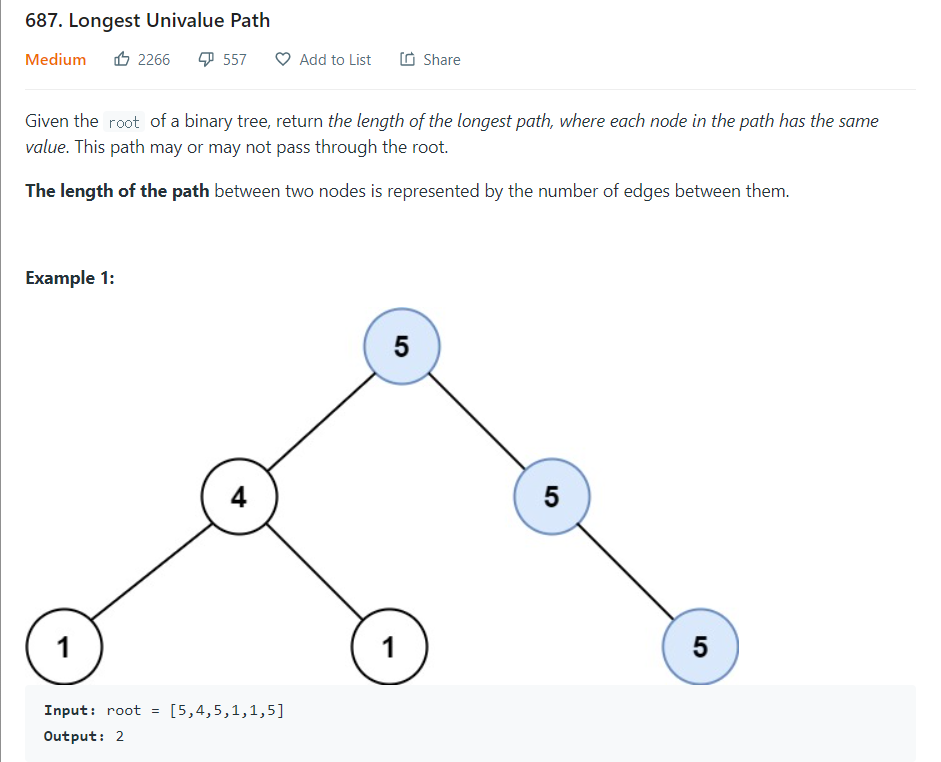
• 동일한 값을 가장 긴 경로를 찾아라.

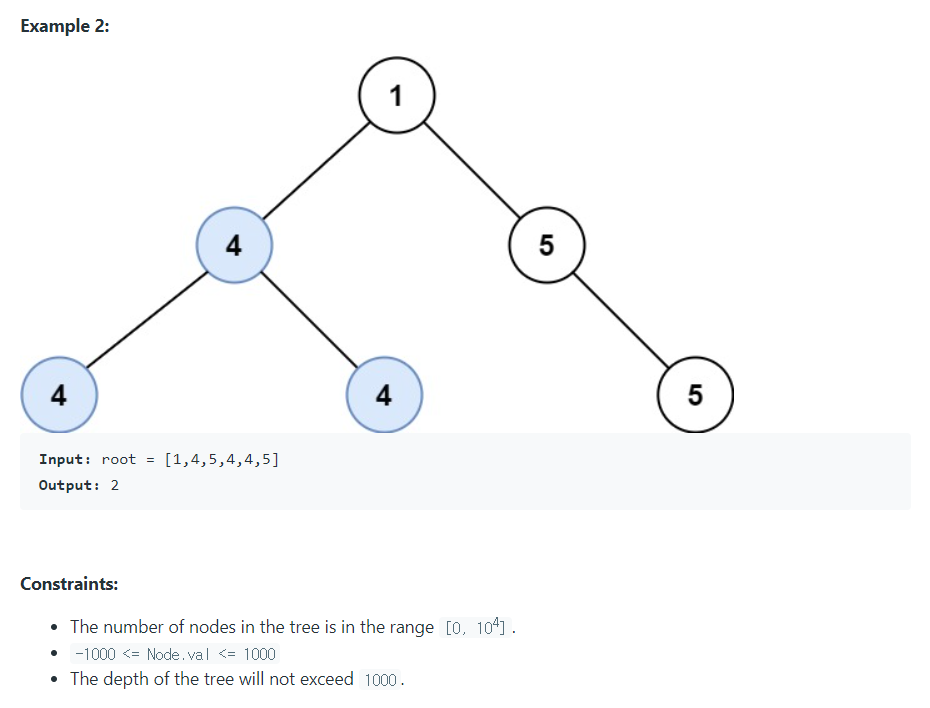
1. 상태값 거리 계산 DFS

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    result: int = 0
        
    def longestUnivaluePath(self, root: TreeNode) -> int:
        def dfs(node: TreeNode):
            if node is None:
                return 0
            
            #존재하지 않는 노드까지 DFS 재귀 탐색
            left = dfs(node.left)
            right = dfs(node.right)
            
            #현재 노드가 자식 노드와 동일한 경우 거리 1 증가
            if node.left and node.left.val == node.val:
                left += 1
            else:
                left = 0
                
            if node.right and node.right.val == node.val:
                right += 1
            else:
                right = 0
                
            #왼쪽과 오른쪽 자식 노드 간 거리의 합 최댓값이 결과
            self.result = max(self.result, left+right)
            #자식 노드 상태값 중 큰 값 리턴
            return max(left, right)
        
        dfs(root)
        return self.result

• 트리의 말단, 리프노드까지 DFS로 탐색해 내려간 다음, 값이 일치할 경우 다음과 같이 거리를 차곡차곡 쌓아 올려가며 백트래킹하는 형태로 풀이할 수 있다.

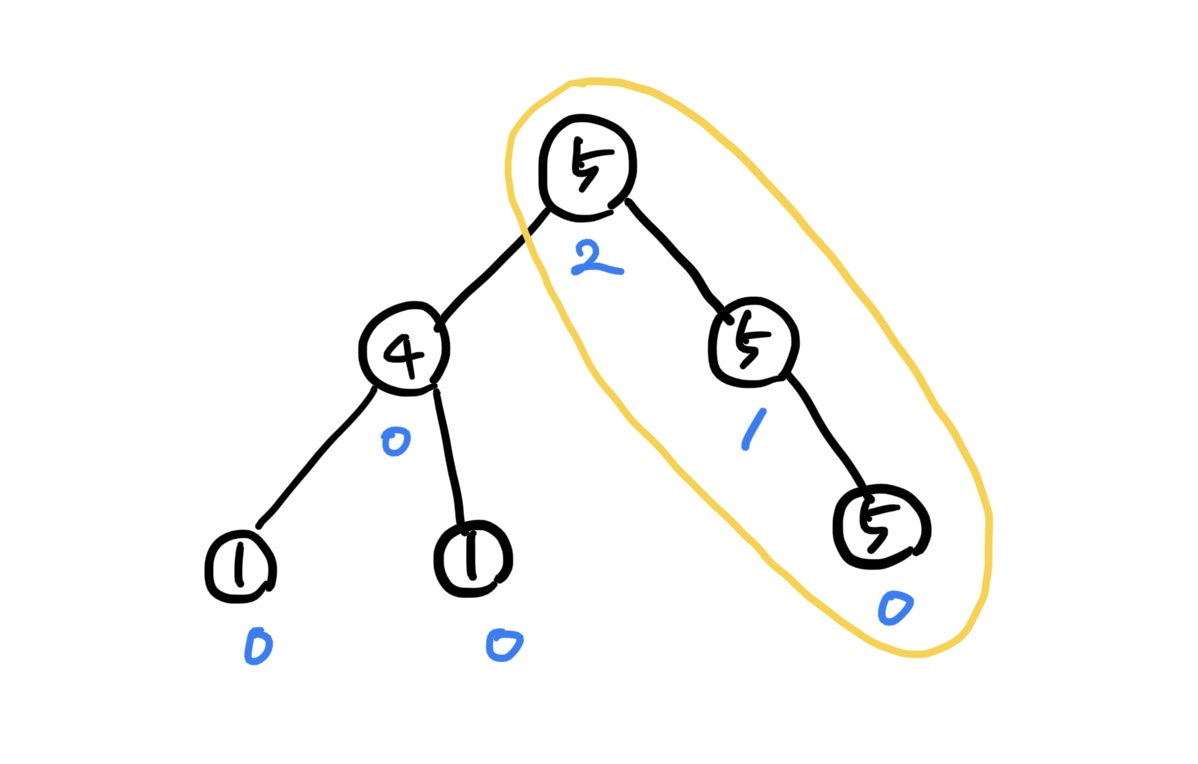
<동일한 값의 이동거리 계산>

• 예제의 첫 번째 입력값을 기준으로 트리를 나타내고, 루트 노드부터 우측 리프 노드까지 이동 거리를 구하는 과정을 표현

• 루트 노드에서부터 DFS로 재귀 탐색을 진행하면서 리프에 도달하면 그 때부터 백트래킹하면서 거리를 누적해 나간다.

• 먼저, DFS 재귀 탐색을 한다.

  • 이렇게 재귀 호출로 내려가면 left, right는 각각 리프노드에 이르러서 값을 리턴받게 된다.

  • 더 이상 존재하지 않는 노드까지 내려가게 되면 다음과 같은 형태로 값을 리턴한다.
    if node is None: return 0

    • 존재하지 않는 노드까지 내려가게 되면 거리 0을 리턴한다.

    • 이 값이 점점 백트래킹되면서 증가할 것이다.

• 이 문제는 동일 값(Univalue) 여부를 판별해 거리를 계산하는 문제이기 때문에, 자식 노드가 동일한 값인지 확인하는 과정이 필요하다.

  • 왼쪽과 오른쪽 자식 노드를 각각 확인해서 현재 노드, 그러니까 부모 노드와 동일한 경우 각각 거리를 1 증가한다.

  • 왼쪽 자식과 오른쪽 자식 노드 간 거리의 합을 결과로 한다.

    • 합이 가장 큰 값을 최종 결과로 한다.

• 다음번 백트래킹 시 계산을 위해 앞서 문제와 유사하게 상태값을 셋팅해서 부모 노드로 올려야 한다.

  • 부모 노드를 위해 현재까지의 거리를 리턴해준다.
    return max(left, right)

• 지금까지 합의 최댓값을 계산해왔기 때문에 상태값도 합인 left + right를 리턴해야 할 것 같다.

  • 그러나, 현재 노드는 양쪽 자식 노드를 모두 연결할 수 있지만 현재 노드의 부모 노드에서는 지금의 양쪽 자식 노드를 동시에 연결할 수 없다.

  • 단방향이므로 양쪽 자식 노드 중 어느 한쪽 자식만 택할 수 있으며, 이는 트리의 특징이기도 하다.

    • 따라서 둘 중 큰 값을 상태값으로 리턴해준다.