45. Invert Binary Tree

리트코드

"재귀도 당장은 음수의 개념처럼 직관적이지 않겠지만 꾸준히 학습하면 자연스럽게 직관이 생겨난다. 그것이 바로 우리가 꾸준히 공부하는 이유며, 알고리즘을 공부하는 이유다. 궁극적으로 더 좋은 코드를 작성할 수 있는 능력이다."

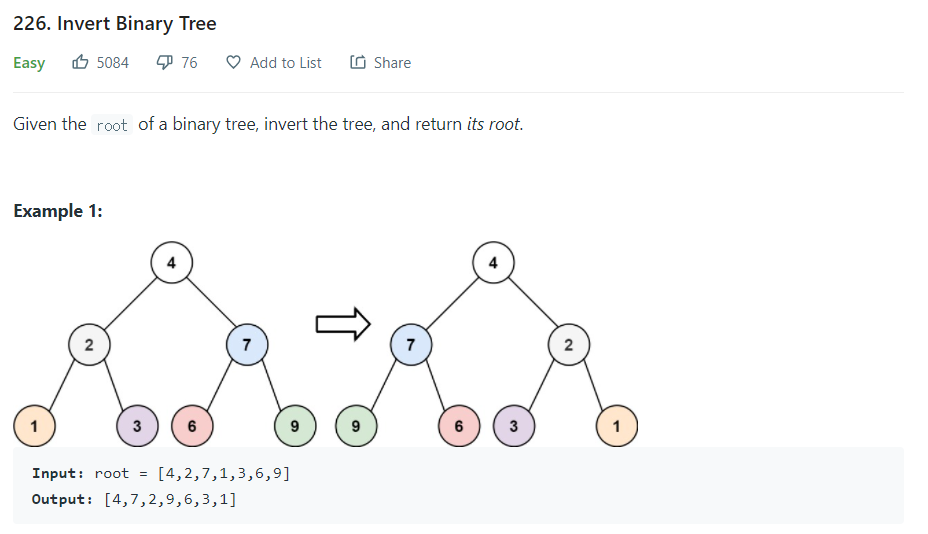
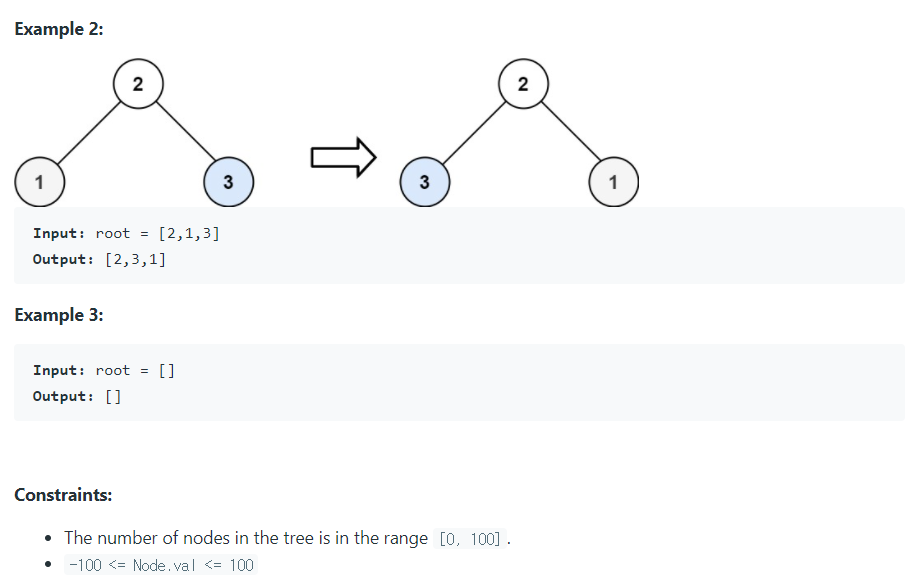
1. 파이썬다운 방식 (28ms)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if root:
            root.left, root.right = \
                self.invertTree(root.right), self.invertTree(root.left)
            return root
        return None

• 이 문제는 파이썬 다운 방식으로 정말 쉽게 풀 수 있다.

  • 막상 설명은 쉽지 않다.

<재귀를 이용한 이진 트리 반전>

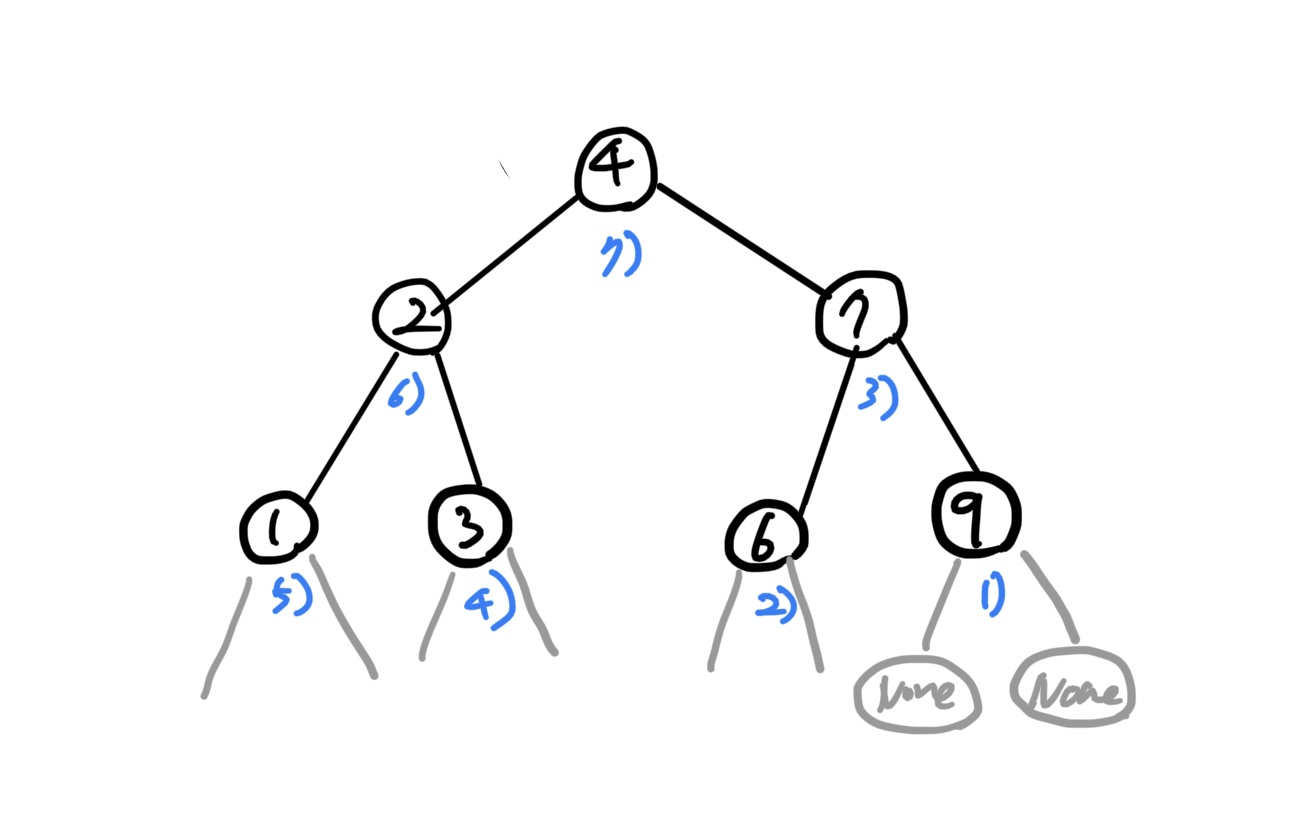
• 이 그림에서는 루트 노드인 4에서 시작하되, 지금까지와는 달리 여기서는 오른쪽부터 재귀 탐색을 진행한다.

  • self.invertTree의 파라미터로 root.right를 먼저 넘겼기 때문이다.

• 노드 9에서 첫 번째 스왑이 일어나고 (실제로는 그 자식인 None까지 탐색하다가 None을 리턴받은 이후에), 두 번째는 노드 6에서 스왑이 일어난다.

• 오른쪽 노드가 다 스왑된 이후에는 왼쪽 노드가 동일한 형태로 스왑된다.

• 마지막 7)번, 루트 노드 4의 자식 노드 간 최종 스왑이 이루어지기 직전의 상태는 다음과 같다.

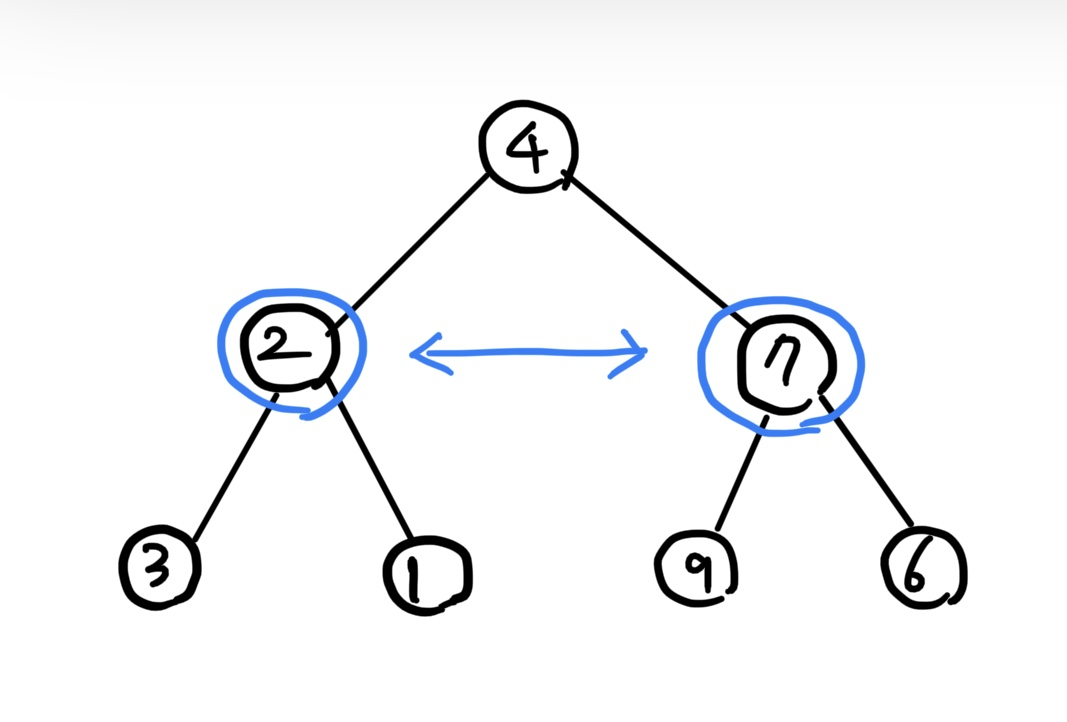
  • 루트 노드 4의 자식 노드 2와 7이 마지막으로 스왑되면서 전체 트리가 반전된다.

➕ 참고로 마지막 return None은 생략이 가능하다.

• 아무것도 리턴하지 않으면 자바나 C++은 당연히 에러를 내뱉겠지만 파이썬은 자연스럽게 None을 할당하기 때문이다.

  • 이 또한 동적 타이핑(Dynamic Typing)언어인 파이썬의 강력한 기능이다.

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if root:
            root.left, root.right = \
                self.invertTree(root.right), self.invertTree(root.left)
            return root

2. 반복 구조로 BFS (24ms)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        queue = collections.deque([root])
        
        while queue:
            node = queue.popleft()
            
            #부모 노드부터 하향식 스왑
            if node:
                node.left, node.right = node.right, node.left
                
                queue.append(node.left)
                queue.append(node.right)
        return root

• 앞서 이진 트리의 최대 깊이 문제는 while구문 내부에 별도의 for문이 있어 부모 노드에 대해 따로 반복해야 했는데, 여기서는 그런 제약이 없어 자유롭게 스왑하면서 queue에 추가한다.

  • 먼저 삽입된 노드는 반복 구조로 계속 스왑되면서 자식 노드가 계속해서 큐에 추가되는 구조가 된다.

• 앞서 재귀 풀이가 가장 말단, 리프노드까지 내려가서 백트래킹하면서 스왑하는 상향(Bottom-Up) 방식이라면, 이 풀이는 부모 노드부터 스왑하면서 계속 아래로 내려가는 하향(Top-Down) 방식 풀이라 할 수 있다.

3. 반복 구조로 DFS (24ms)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        stack = collections.deque([root])
        
        while stack:
            node = stack.pop()
            
            #부모 노드부터 하향식 스왑
            if node:
                node.left, node.right = node.right, node.left
                stack.append(node.left)
                stack.append(node.right)
        return root

• BFS로 탐색할 때는 popleft()로 처음 값을 추출했고, 여기서 DFS로 탐색할 때는 pop()으로 마지막 값을 추출했다.

• 변수명을 stack으로 바꾼건 다소 형식적이다.

  • 어차피 데크는 이중 연결 리스트이기 때문에 스택에도, 큐에도 자유롭게 활용이 가능하다.

4. 반복 구조로 DFS 후위 순회 (24ms)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        stack = collections.deque([root])
        
        while stack:
            node = stack.pop()
            
            #부모 노드부터 하향식 스왑
            if node:
               
                stack.append(node.left)
                stack.append(node.right)
                
                node.left, node.right = node.right, node.left #후위 순회
        return root
        

• 전위 순회와 스왑 위치만 다를 뿐 모든 게 동일하다.