48. Balanced Binary Tree

리트코드

• 이진 트리가 높이 균형(Height-Balanced)인지 판단하라.

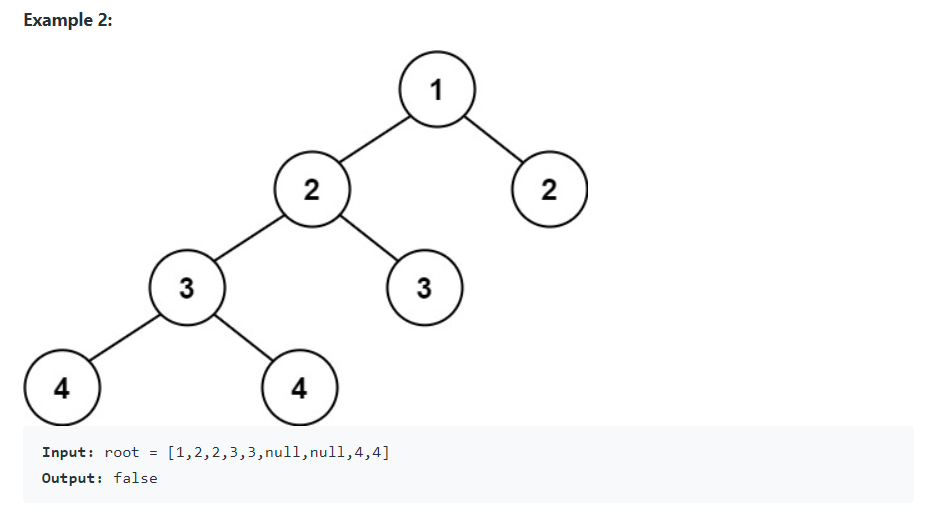
1. 재귀 구조로 높이 차이 계산

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def check(root):
            if not root:
                return 0
            
            left = check(root.left)
            right = check(root.right)
            
            #높이 차이가 나는 경우 -1, 이외에는 높이에 따라 1 증가
            if left == -1 or \
                    right == -1 or \
                    abs(left - right) > 1:
                return -1
            
            return max(left, right) + 1
        
        return check(root) != -1
        

• 높이 균형은 매우 중요한 개념이다. 균형이 맞아야 효율적으로 트리를 구성할 수 있으며, 탐색 또한 훨씬 더 효율적으로 처리할 수 있기 때문이다.

  • 높이 균형을 매번 맞추는 AVL 트리는 대표적인 자가 균형 이진 탐색 트리이기도 하다.

• 여기서는 높이 균형이 맞는지 여부를 판별하는 코드를 구현해본다.

  • 판별 함수 isBalaced()의 뼈대를 만든다.

• 재귀 호출로 리프 노드까지 내려간다.

  • 맨 마지막 노드에 이르면 각각 left = 0, right = 0을 리턴하도록 구성된다.

• check() 함수를 살펴보자.

  • left와 right가 모두 0 이라면, 차이가 1보다 크지 않으므로 max(left, right) + 1로 1을 리턴하게 된다.

  • 이런식으로 점점 1씩 증가하는 형태가 된다.

• 예제에서 false로 처리된 입력값 [1,2,2,3,3,null,null,4,4]를 대상을 표현한 그림을 살펴보자.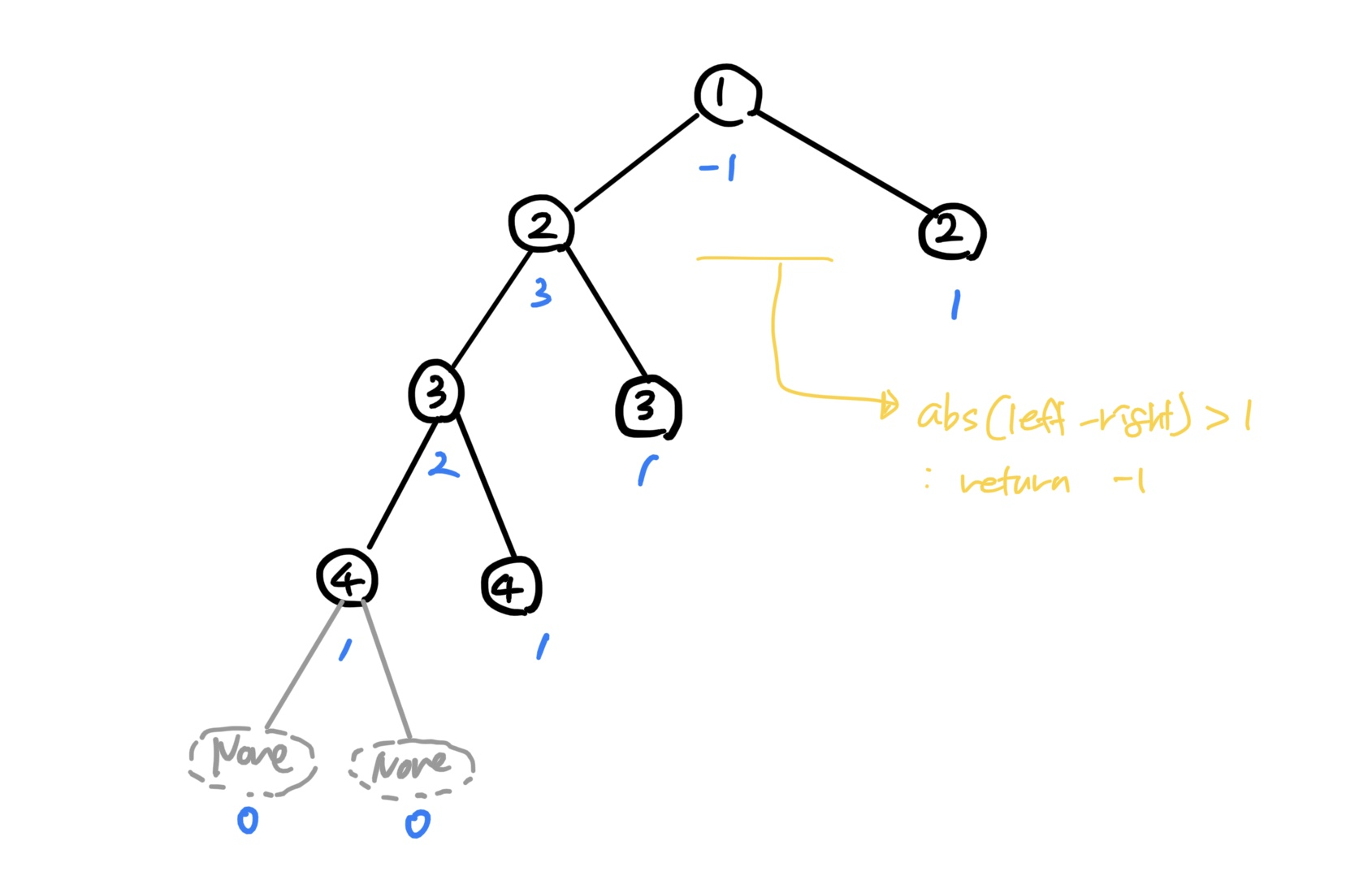

  

  • 리프 노드인 4는 1, 그 부모 노드인 3은 2, 이런 식을 높이에
    따라 1씩 점점 증가하는 형태를 띤다.

  • 하지만, 루트 1의 오른쪽 자식 노드인 2는 더 이상 자식이 없으므로 값은 1을 받게 된다.

    • 그 왼쪽, 즉 형제 노드는 3이므로 높이 차이가 1을 초과하므로 -1을 리턴 받는다.

    • 즉, 루트는 -1이 된다.

  • 이렇게 한번 -1이 되면 더 이상 회복이 되지 않는다.

    • 만약 부모 노드가 또 있다해도 그 오른쪽 노드는 어떠한 경우에도 1 이상의 값을 갖게 될 것이므로 계속해서 높이 차이가 1을 초과한다.

      때문에 마찬가지로 -1을 리턴받는다.

    • 즉, 양쪽 자식 노드 중 어느 하나가 -1이 되는 경우에는 계속해서 -1을 리턴하게 되며,

      각 서브트리의 높이 차이가 한 번이라도 1을 초과하는 경우 -1이 할당되며 계속해서 부모 노드로 -1을 리턴하다 최종적으로 False를 리턴하게 된다.