49. Minimum Height Trees

리트코드

• 노드 개수와 무방향 그래프를 입력받아 트리가 최소 높이가 되는 루트의 목록을 리턴하라.

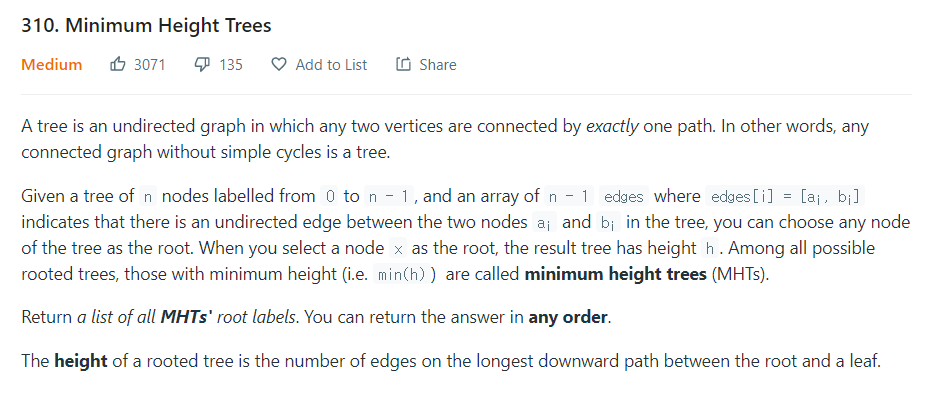
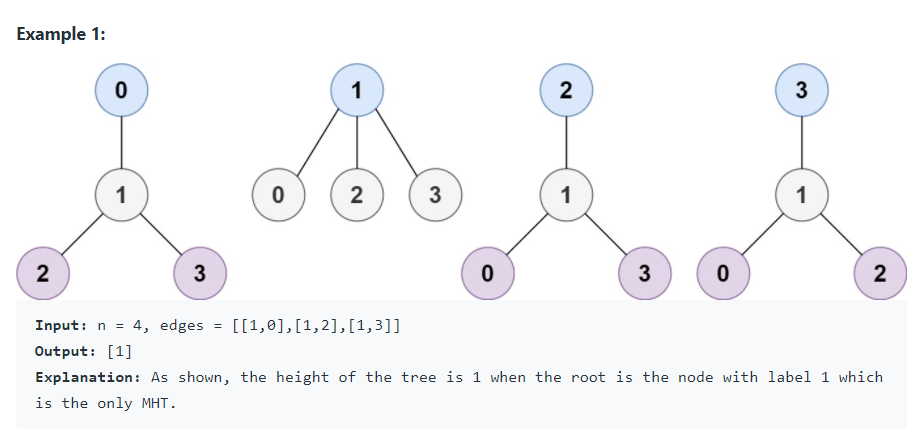
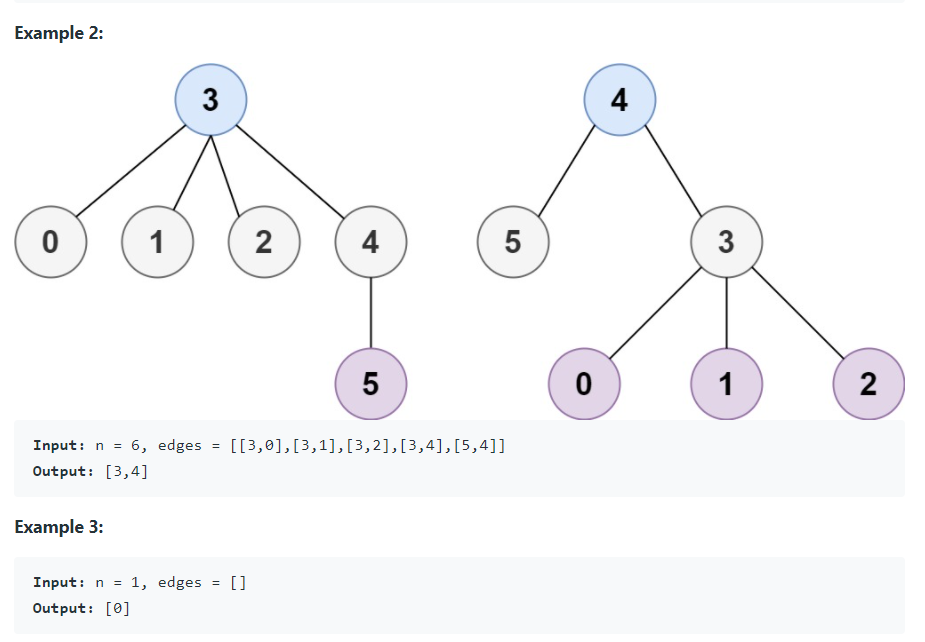
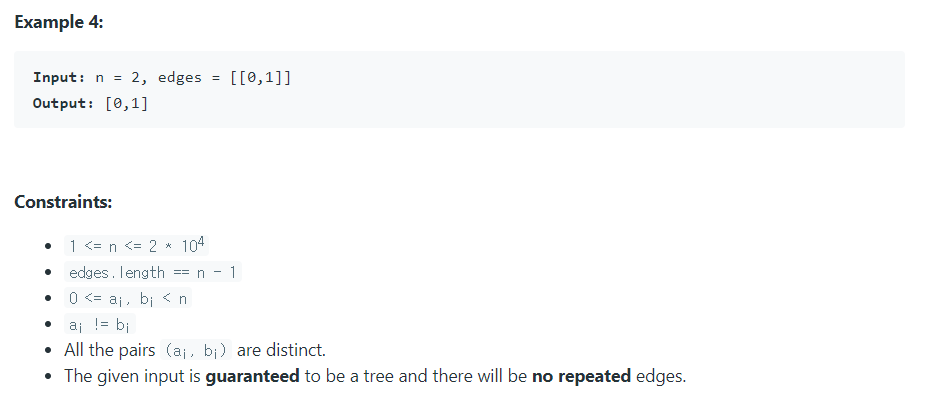
1. 단계 별 리프 노드 제거

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        if n <= 1:
            return [0]
        
        #양방향 그래프 구성
        graph = collections.defaultdict(list)
        for i, j in edges:
            graph[i].append(j)
            graph[j].append(i)
            
        #첫 번째 리프 노드 추가
        leaves = []
        for i in range(n + 1):
            if len(graph[i]) == 1:
                leaves.append(i)
        
        #루트 노드만 남을 때까지 반복 제거
        while n>2:
            n -= len(leaves)
            new_leaves = []
            for leaf in leaves:
                neighbor = graph[leaf].pop()
                graph[neighbor].remove(leaf)
                
                if len(graph[neighbor]) == 1:
                    new_leaves.append(neighbor)
            
            leaves = new_leaves
        
        return leaves

• 최소 높이를 구성하려면 가장 가운데에 있는 값이 루트여야 한다.

  • 리프 노드를 하나씩 제거해 나가면서 남아 있는 값을 찾으면 이 값이 가장 가운데에 있는 값이 될 것이고, 이 값을 루트로 했을 때 최소 높이를 구성할 수 있다는 뜻이기도 하다.

• 입력값이 [[1, 3], [2, 3], [3, 4], [3, 5], [4, 6], [6, 10], [5, 7], [5, 8], [8, 9]] 와 같을 때 그래프를 구성해 본다.
  

• 여기서부터 리프 노드를 제거해 본다.

  • 가장 가운데에 있는, 가장 마지막에 남을 루트가 될 노드는 어떤 노드가 될지 상상해본다.
    

  • 1, 2, 7, 9, 10인 리프 노드를 한 번 제거했다.

    

  • 6, 8인 두 번째 리프 노드를 제거했다.

    • 이제 어떤 값이 남아서 루트가 될지 어렴풋이 알 수 있을 것이다.
    

  • 리프 노드를 세 번째 제거했고 결과는 하나가 남았다.

  
  
  • 최종 결과는 3이고, 3을 루트로 했을 때 최소 높이 트리를 구성할 수 있을 것이다.

• 이제 코드로 이를 구현해 보자.

  • 이 문제에서 그래프는 무방향(Undirected)이므로, 트리의 부모와 자식은 양쪽 노드 모두 번갈아 가능하다.

  • 따라서, 양쪽 모두 graph라는 이름의 그래프 딕셔너리 변수에 양방향으로 삽입하여 구성한다.

• 리프 노드를 찾아서 leaves에 추가한다.

  • 리프 노드는 그래프에서 해당 키의 값이 1개 뿐인 것을 말한다.

leaves = []
        for i in range(n + 1):
            if len(graph[i]) == 1:
                leaves.append(i)

• graph의 값을 출력해보면 다음과 같다.

>>>graph

defaultdict(<class 'list'>, {
    1: [3],
    3: [1, 2, 4, 5],
    2:[3],
    4: [3, 6],
    5: [3, 7, 8],
    6: [4, 10],
    10: [6],
    7: [5],
    8: [5, 9],
    9: [8]
})

• 입력값 [[1, 3], [2, 3], [3, 4], [3, 5], [4, 6], [6, 10], [5, 7], [5, 8], [8, 9]] 를 딕셔너리로 표현한 그래프의 값은 이런 형태가 되고, 이 중에서 값이 1개뿐인 [1, 2, 10, 7, 9]가 첫 번째 리프 노드로 leaves 리스트 변수에 담기게 된다.

  • 그림에서 리프 노드를 한 번 제거한 모습과 leaves에 담긴 리프 노드들이 동일함을 확인할 수 있다.

• 이제 루트가 남을 때까지 반복해서 계속 제거한다.

• n은 전체 노드의 개수이므로 여기서 leaves, 즉 리프 노드의 개수만큼 계속 빼나가면서 최종 2개 이하가 남을때까지 반복한다.

  • 마지막에 남은 값이 홀수 개일때는 루트가 최종 1개가 되지만, 짝수 개일때는 2개가 될 수 있다. 따라서 while 반복문은 2개까지는 계속 반복한다.

    • 리프노드는 반복하면서 제거한다.

    • 그래프 딕셔너리에서 pop()으로 제거하고, 연결된 값도 찾아서 제거한다.

      • 무방향 그래프라 그래프를 각각 두번씩 만들었으므로 제거 또한 두 번씩 진행한다.

  • 계속 반복하면서 leaves에 최종적으로 2개 이하의 노드가 남게 되었을 때, 이 노드들이 루트가 되며 최종 결과로 리턴한다.