50. Convert Sorted Array to Binary Search Tree

리트코드

• 오름차순으로 정렬된 배열을 높이 균형(Height Balanced) 이진 탐색 트리로 변환하라.

• 이 문제에서 높이 균형이란 모든 노드의 두 서브 트리 간 깊이 차이가 1 이하인 것을 말한다.

  • 정렬된 배열 [-10,-3,0,5,9]이 주어졌을 때, 가능한 답변은 [0,-3,9,-10,null,5] 이며, 이와 같은 높이 BST(이진 탐색 트리)로 나타낼 수 있다.

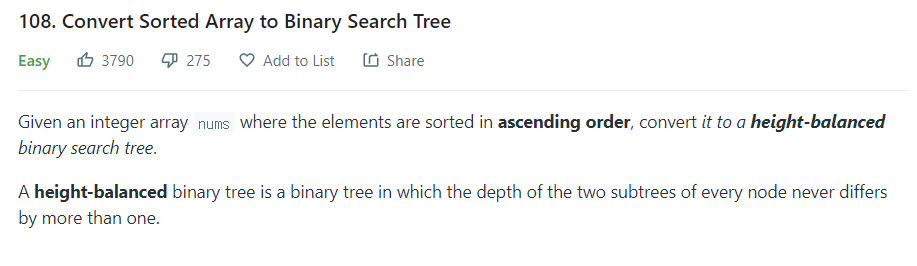
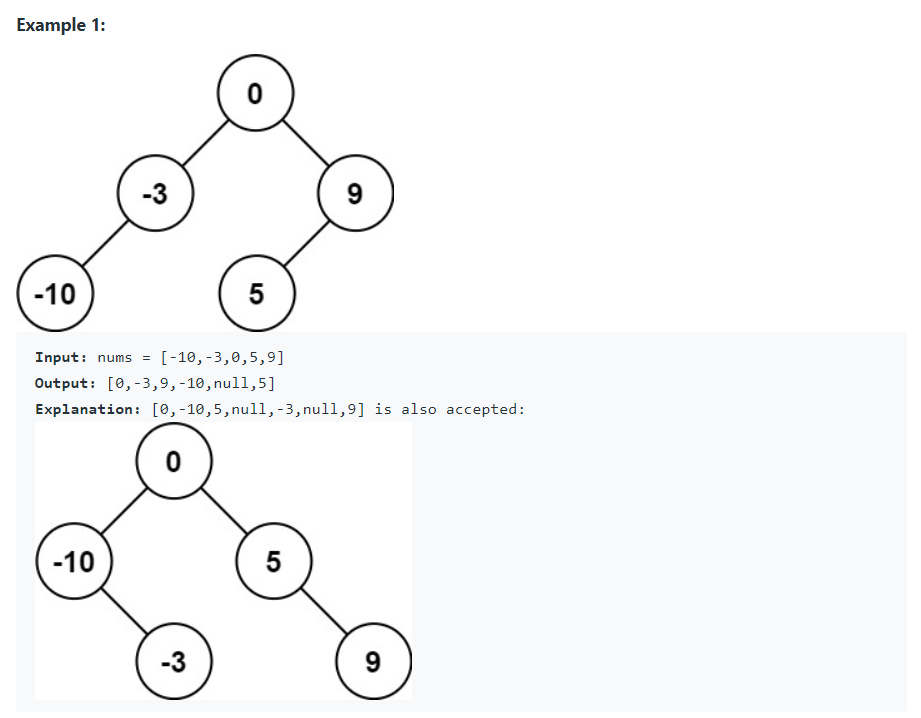
1. 이진 검색 결과로 트리 구성

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        if not nums:
            return None
        
        mid = len(nums) //2

        #분할 정복으로 이진 검색 결과 트리 구성
        node = TreeNode(nums[mid])
        node.left = self.sortedArrayToBST(nums[:mid])
        node.right = self.sortedArrayToBST(nums[mid + 1:])

        return node
        

• 이 문제를 제대로 풀이하기 위해서는 먼저 이진 탐색 트리, 그러니까 BST의 특징에 대해 정확하게 파악하고 있어야 한다.

  • BST를 만들기 위해서는 정렬된 배열을 이진 검색으로 계속 쪼개 나가기만 하면 된다.

  • 정렬되어 있지 않으면 사용할 수 없다.

  • 이진 검색 자체가 정렬된 배열에서는 어떤 값이든지 간에 log(n)에 찾아낼 수 있는 마법이고, 동일한 이름의 BST 또한 당연히 정렬된 배열을 기준으로 한다.

• 예제의 입력값 외에 완전 이진 트리(Complete Binary Tree) 형태가 될 수 있도록 해 보면 다음과 같다.

  

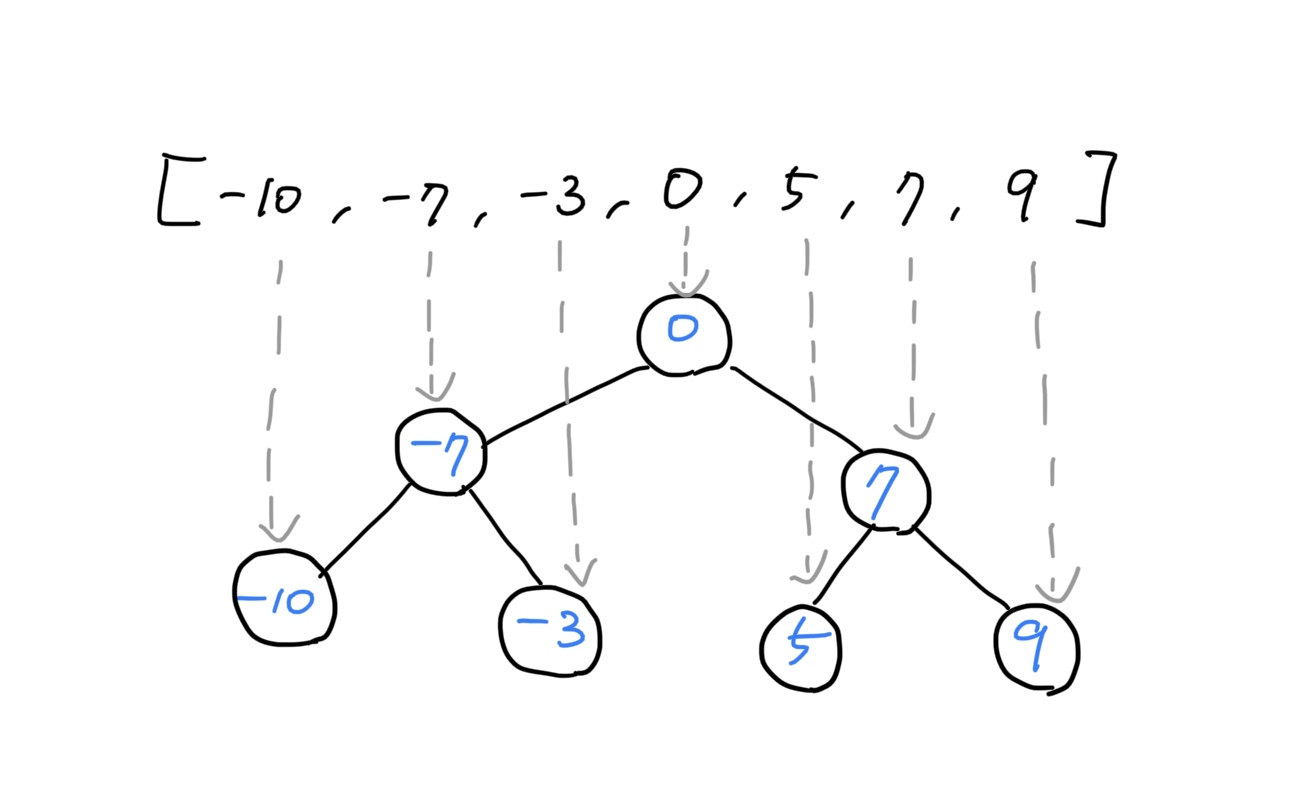
  • 이 그림에서는 정확히 한 번의 이진 검색 결과가 각각의 노드로 구성된다.

    • 즉 0이 가장 먼저, 그 다음은 -7, 7 ... 이런 식으로 구성되면서 내려간다.

    • 이진 검색을 할 때마다 그 값이 노드로 구성됨을 알 수 있다.

• 정확히 중앙값을 갖도록 내림값을 리턴하는 // 연산자를 사용했다.

  • 즉 lens(nums)가 3이라면, 2를 나눈 결과인 1.5에서 내림하여 1이 된다.

  • 인덱스는 0부터 시작하기 때문에 1은 [0, 1, 2]에서 정확히 중앙값이 된다.

    • 왼쪽 자식은 남은 절반을 재귀 호출로 계속 처리하고, 오른쪽 자식 또한 마찬가지로 처리한다.

• 파이썬의 슬라이스 기능을 이용하면 매우 간단하게 코드로 구현할 수 있으며, 절반씩 분할해 처리되는 분할 정복 구조로 처리된다.

  • 끝까지 처리되면 배열은 정확히 높이 균현 BTS가 될 것이다.