52. Range Sum of BST

리트코드

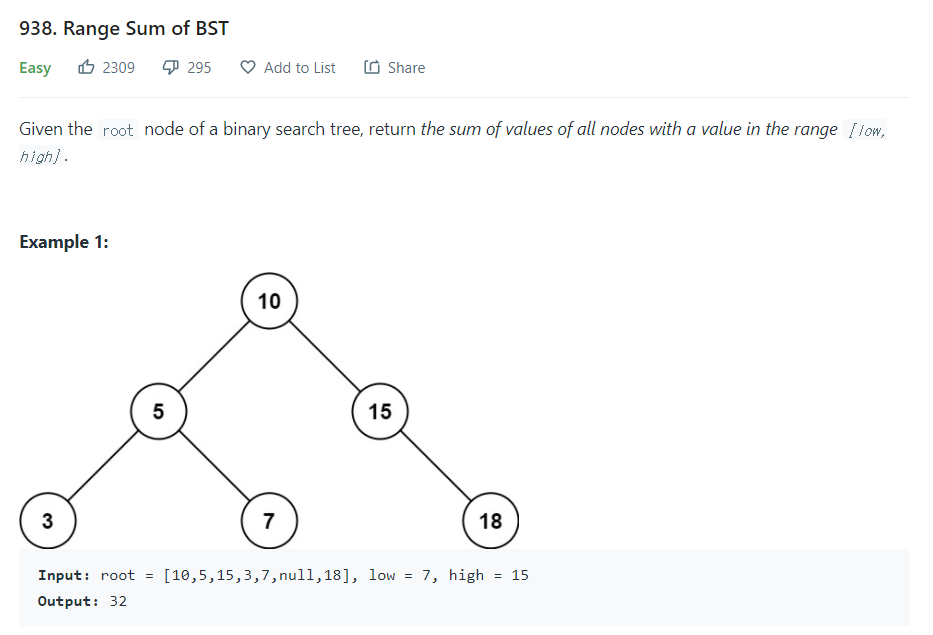
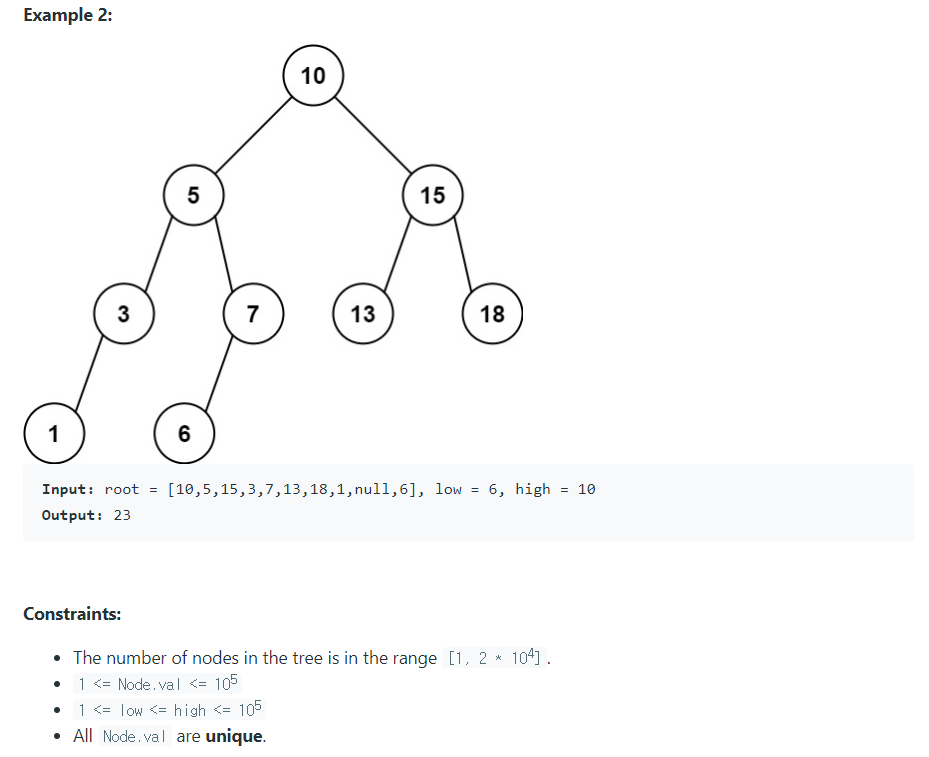
• 이진 탐색 트리(BST)가 주어졌을 때 L 이상 R 이하의 값을 지닌 노드의 합을 구하라.

1. 재귀 구조 DFS로 브루트 포스 탐색 (288ms)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        if not root:
            return 0
        
        return (root.val if low <= root.val <= high else 0 ) + \
                self.rangeSumBST(root.left, low, high) + \
                self.rangeSumBST(root.right, low, high)

<L 이상 R 이하 값을 지닌 노드의 합>

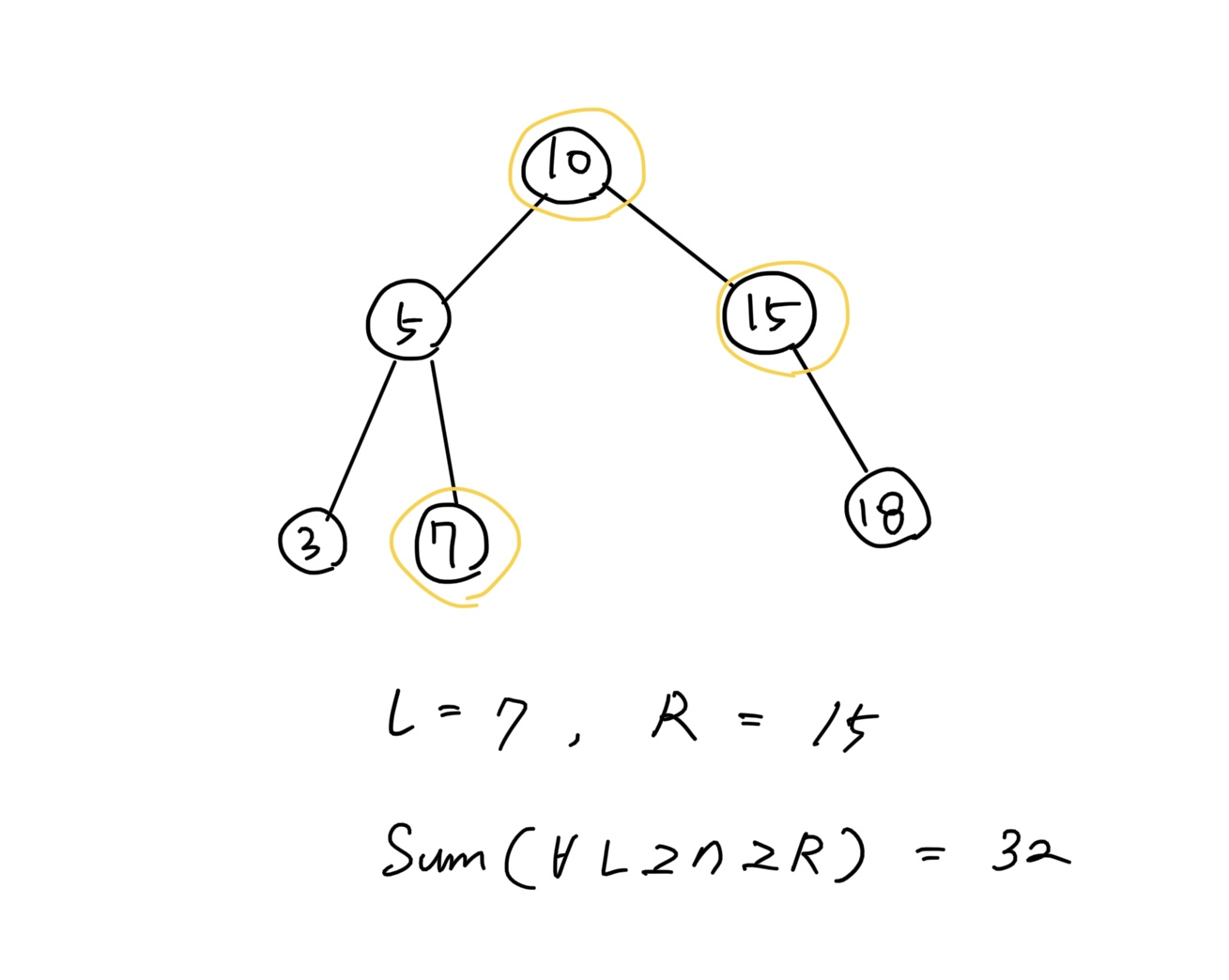
• 이 그림에서 L=7, R=15일 때 L 이상, R 이하인 노드는 자기 자신을 포함해 7, 10, 15이며, 이들의 합 sum()은 32이다.

• 이 문제는 DFS로 전체를 탐색한 다음, 노드의 값이 L(low)과 R(high)사이일 때만 값을 부여하고, 아닐 경우에는 0을 취해 계속 더해 나가면 쉽게 구할 수 있다.

2. DFS 가지치기로 필요한 노드 탐색 (224ms)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        def dfs(node: TreeNode):
            if not node:
                return 0
            
            if node.val < low:
                return dfs(node.right)
            elif node.val > high:
                return dfs(node.left)
            return node.val + dfs(node.left) + dfs(node.right)
        return dfs(root)
        

• DFS로 탐색하되 low, high 조건에 해당되지 않는 가지(Branch)를 쳐내는(Pruning) 형태로 탐색에서 배제하도록 구현한다.

• 이진 탐색 트리는 왼쪽이 항상 작고, 오른쪽이 항상 크다.

  • 즉 현재 노드 root가 low보다 작을 경우, 더 이상 왼쪽 가지는 탐색할 필요가 없기 때문에 오른쪽만 탐색하도록 재귀 호출을 리턴한다.

  • high보다 클 경우, 오른쪽은 더 이상 탐색할 필요가 없으므로 왼쪽만 탐색하도록 재귀 호출을 리턴한다.

• 이렇게 불필요한 탐색을 줄여 최적화 할 수 있다.

3. 반복 구조 DFS로 필요한 노드 탐색 (220ms)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        stack, sum = [root], 0
        
        #스택 이용 필요한 노드 DFS 반복
        while stack:
            node = stack.pop()
            if node:
                if node.val > low:
                    stack.append(node.left)
                if node.val < high:
                    stack.append(node.right)
                if low <= node.val <= high:
                    sum += node.val
        return sum
        

• 대부분의 재귀 풀이는 반복으로 변경할 수 있다.

  • 일반적으로 반복 풀이가 재귀 풀이에 비해 좀 더 직관적으로 이해가 쉽다.

• 마찬가지로 유효한 노드만 스택에 계속 집어 넣으면서, low와 high 사이의 값인 경우 값을 더해 나간다.

  • 유효한 노드만 삽입하기 때문에 앞서 풀이인 가지치기기와 탐색 범위가 유사하며, 스택이므로 DFS와 동일한 탐색 구조를 띤다.

4. 반복 구조 BFS로 필요한 노드 탐색 (232ms)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int:
        stack, sum = [root], 0
        
        #큐 연산을 이용해 반복구조 BFS로 필요한 노드 탐색
        while stack:
            node = stack.pop(0)
            if node:
                if node.val > low:
                    stack.append(node.left)
                if node.val < high:
                    stack.append(node.right)
                if low <= node.val <= high:
                    sum += node.val
        return sum
        

• BFS로 탐색해도 동일하다. 여기서는 스택을 단순히 큐 형태로 바꾸기만 하면, BFS를 구현할 수 있다.

  • 파이썬의 데크를 사용해야 성능을 높일 수 있지만, 여기서는 편의상 간단히 리스트를 그냥 pop(0)로 처리하는 정도로 다음과 같이 BFS를 구현하고, 마찬가지로 동일하게 정답을 풀이할 수 있다.

• 이 문제는 애초에 테스트케이스의 입력값이 크지 않은 것 같다. 입력값이 매우 클 경우 브루트 포스와 가지치기의 속도 차이가 훨씬 더 커야하는데, 생각보다 그다지 크지 않다.

• 마찬가지로 반복 BFS 구현에서 pop(0)은 O(n) 이기 때문에 DFS 구현과 속도 차이가 많이 나야 하는데 (pop()은 O(1)) 그리 많이 나지 않는다.

  • 만약 입력값이 매우 크다면 확연히 다른 성능 차이를 확인할 수 있을 것이다.