53. Minimum Distance Between BST Nodes

리트코드

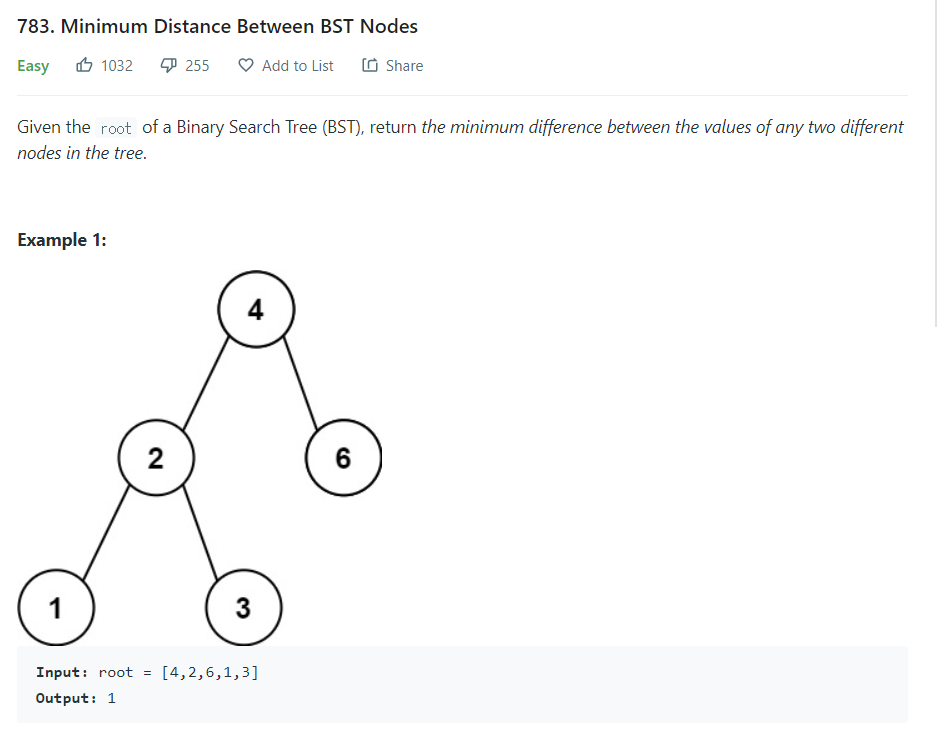
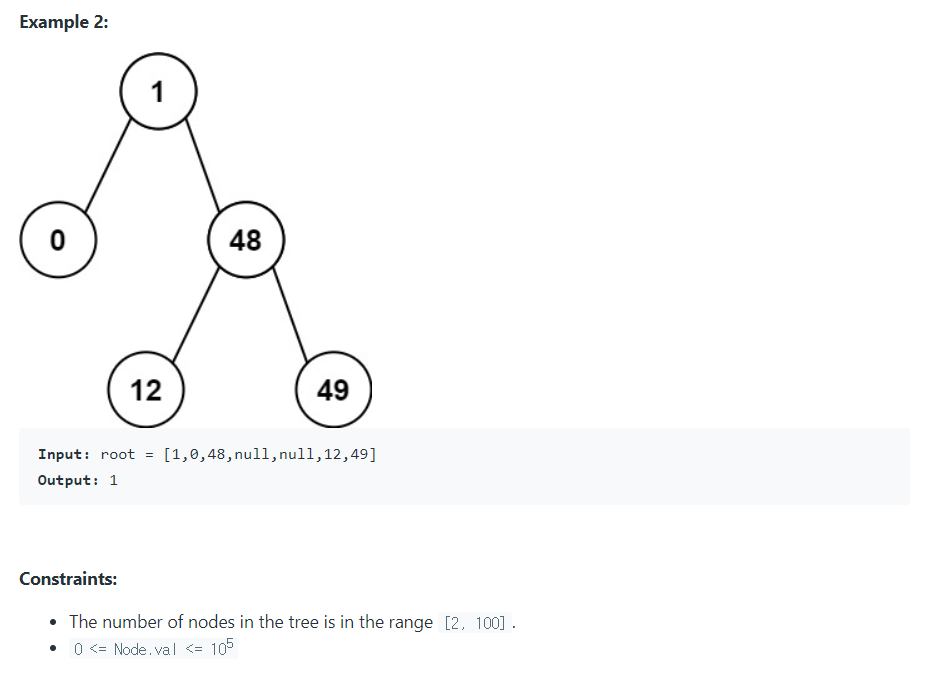
• 두 노드 간 값의 차이가 가장 작은 노드의 값의 차이를 출력하라

1. 재귀 구조로 중위 순회

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    prev = -sys.maxsize
    result = sys.maxsize
    
    #재귀 구조 중위 순회 비교 결과
    def minDiffInBST(self, root: TreeNode) -> int:
        if root.left:
            self.minDiffInBST(root.left)
            
        self.result = min(self.result, root.val - self.prev)
        self.prev = root.val
        
        if root.right:
            self.minDiffInBST(root.right)
            
        return self.result
        

• 값의 차이가 가장 작은 노드를 찾으려면 어디와 어디 노드를 비교해야 하는지 생각해보자.

  • BST의 왼쪽 자식은 항상 루트보다 작고, 오른쪽 자식은 항상 루트보다 크다.

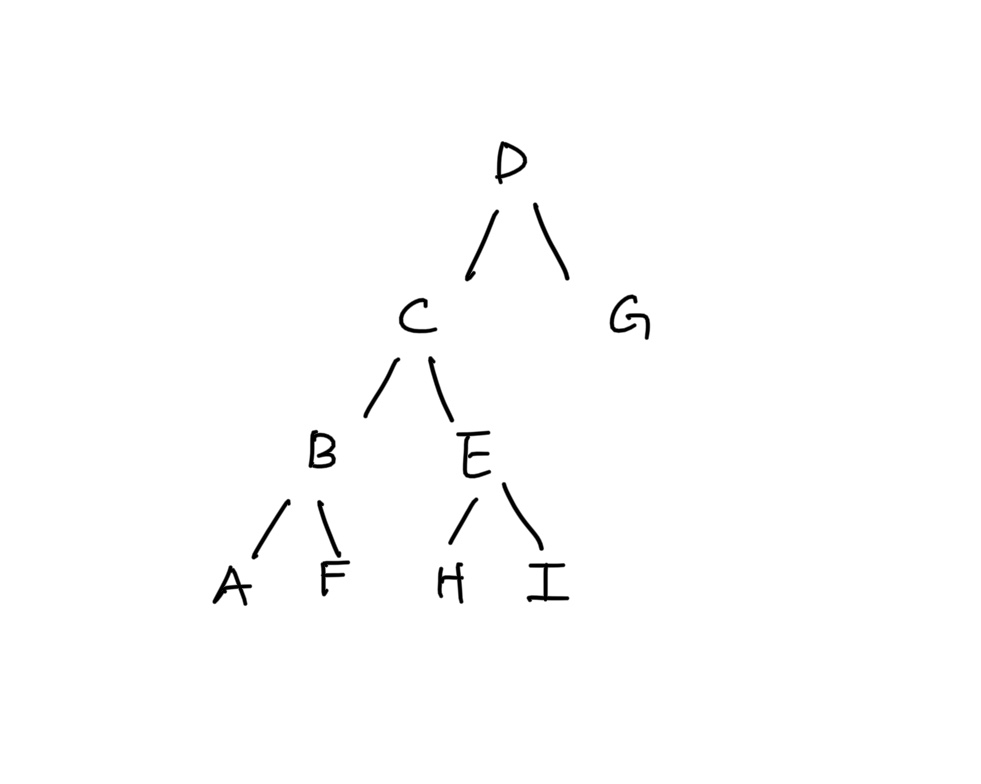
• 이 경우 루트 D와 가장 차이가 작을 수 있는 노드는 딱 2개 노드만 가능한데, 어디와 어디일까?

  • 정답은 I와 G이다.

• 이외에는 항상 이들 노드보다 값의 차이가 클 것이다.

  • D -> B의 차이는 D -> C보다는 무조건 크다. 왼쪽으로 갈수록 값이 더 작아지기 때문이다.

  • D -> A, D -> F 도 마찬가지다. D -> C보다 작아질 수 없다.

  • 따라서 D -> B 부터는 제외하고, 그렇다면 D -> E 하위 노드들에 가능성이 있는데, 이 중에서도 D -> H는 D -> E보다 무조건 크기 때문에 마찬가지로 배제한다.

  • 오른쪽 자식은 더 큰 값을 지니기 때문에 이 경우 D -> I가 가장 작은 값이 될 수 있다.

  • 물론 항상 정답은 아닐 수도 있다. 왜냐면 D -> G가 의외로 가장 작은 값이 될 수 있기 때문이다.

    • 따라서 여기서는 D -> I와 D -> G 중 작은 갑을 택하면 정답이 된다.

  
  
  

<두 노드 간 값의 차이가 가장 작은 노드 계산>

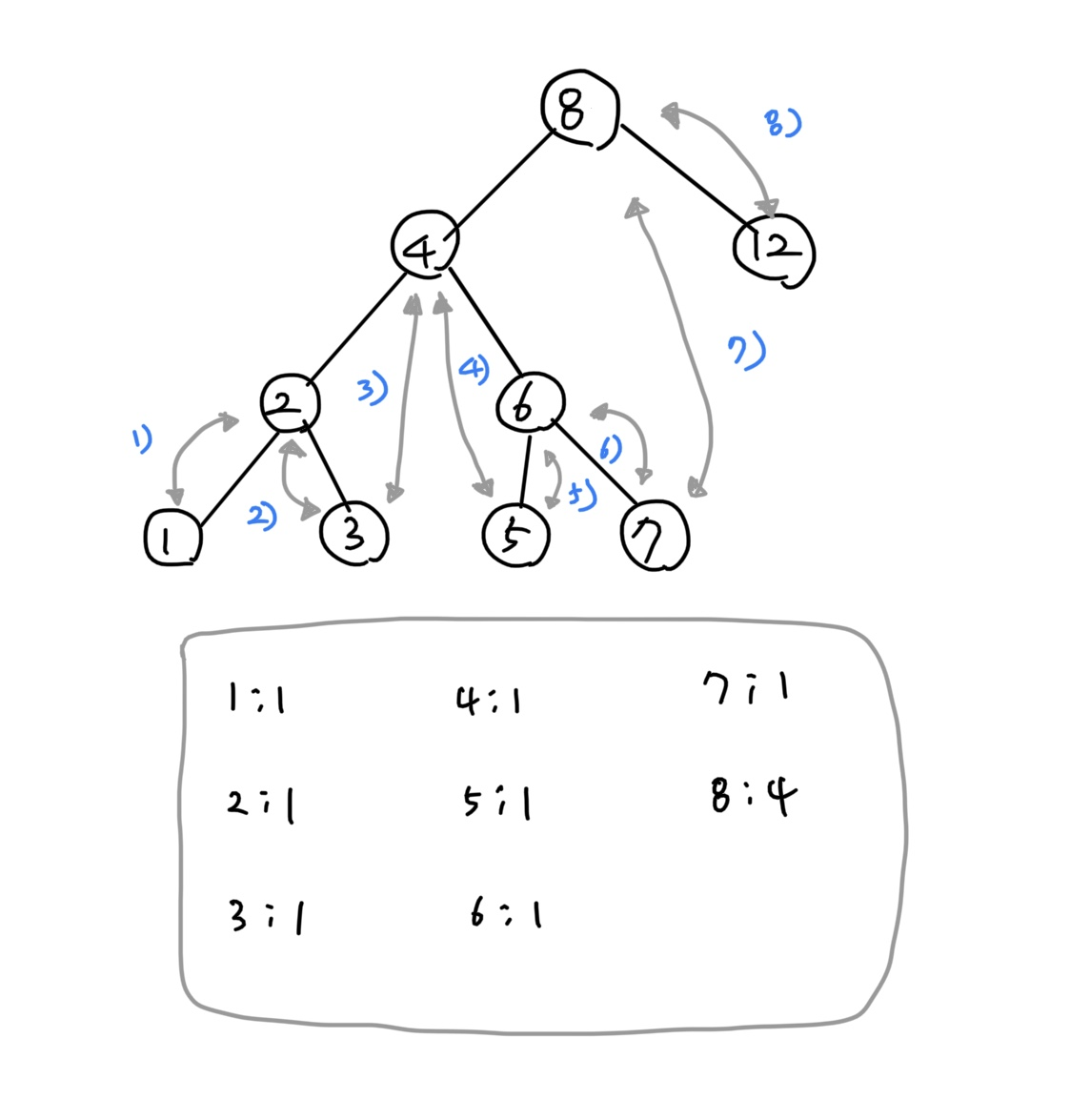
• 두 노드 간 값의 차이가 가장 작은 노드를 계산하기 위한 순서를 파란 글씨로 표시했다.

  • 이 순서대로 탐색하면서 각 거리를 계산해 나가면 값의 차이가 가장 작은 노드의 값을 찾을 수 있다.

• 루트인 8은 7과 12 두 군데를 비교해보는데, 앞서 설명한 D -> I, D -> G인 비교 대상과 동일함을 확인할 수 있다.

  • 여기서 정답은 1이며 이렇게 값의 차이가 1인 노드는 여럿 있다. 그러나 최솟값을 출력하기만 하면 되므로, 중복된 값인 1을 정답으로 출력하면 된다.

• 중위 순회를 하면서 이전 탐색 값과 현재 값을 비교하면 바로 이 순서대로 비교할 수 있을 것 같다.

2. 반복 구조로 중위 순회

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    
    #반복 구조 중위 순회 비교 결과
    def minDiffInBST(self, root: TreeNode) -> int:
        prev = -sys.maxsize
        result = sys.maxsize
    
        stack = []
        node = root
        while stack or node:
            while node:
                stack.append(node)
                node = node.left
            
            node = stack.pop()
            
            result = min(result, node.val - prev)
            prev = node.val
            
            node = node.right
            
        return result

• 추가 장점은 재귀일 때는 prev와 result를 클래스 멤버 변수로 선언했지만, 반복 구조에서는 한 함수 내에서 처리할 수 있기 때문에 함수 내 변수로 선언이 가능하다는 점이다.

• DFS 풀이인 만큼 스택을 사용했고, 오른쪽 자식 노드를 택하기 전에 비교하는 형태로 재귀와 동일하게 중위 순회로 풀이했다.

  • 재귀와 달리 클래스 변수를 사용하지 않아도 되므로, 변수 값의 변화를 추적하기가 쉽고 좀 더 직관적이다.