54. Construct Binary Tree from Preorder and Inorder Traversal

리트코드

• 트리의 전위, 중위 순회 결과를 입력값으로 받아 이진 트리를 구축하라.

1. 전위 순회 결과로 중위 순회 분할 정복

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        if inorder:
            #전위 순회 결과는 중위 순회 분할 인덱스
            
            index = inorder.index(preorder.pop(0))
            
            #중위 순회 결과 분할 정복
            node = TreeNode(inorder[index])
            node.left = self.buildTree(preorder, inorder[0:index])
            node.right = self.buildTree(preorder, inorder[index + 1:])
            
            return node

• 순회에는 크게 전위, 중위, 후위 순회가 있으며 이 셋 중 2가지만 있어도 이진 트리를 복원할 수 있다.

  • 이 문제는 여기서 2가지 결과인 전위와 중위 결과를 받아 이진 트리를 만들어보는 문제다.

• 전위와 중위는 과연 어떤 관계가 있을까

  

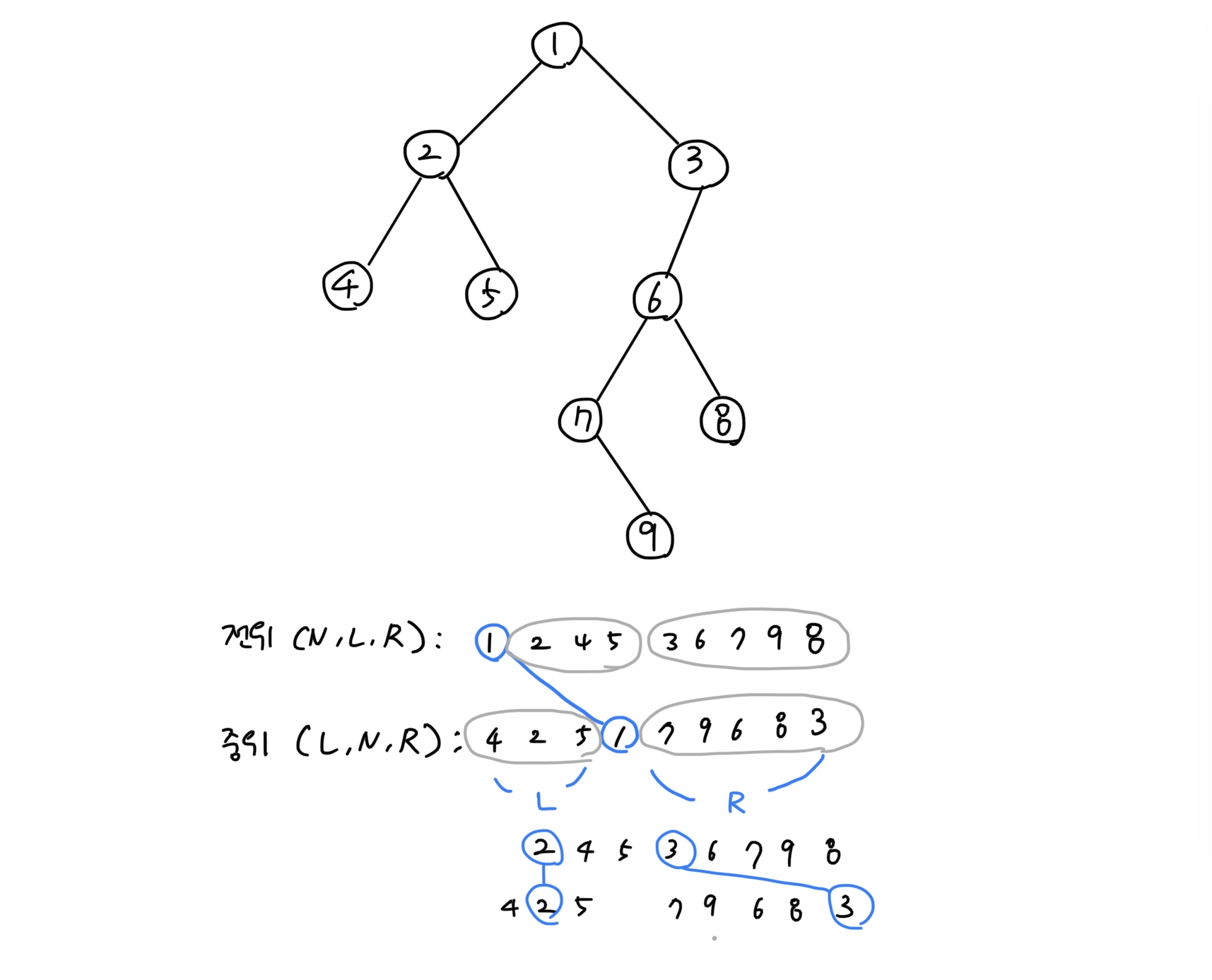
  • 전위의 첫 번째 값은 부모 노드다. 즉 전위 순회의 첫 번째 결과는 정확히 중위 순회 결과를 왼쪽과 오른쪽으로 분할시키는 역할을 한다.

    • 중위 순회의 분할 정복(Divide and Conquer) 문제로 바꾸는 것이다.

  • 두 번째로 왼쪽 노드의 2는 중위 순회 결과를 정확히 반으로 가르고, 각각 왼쪽 자식은 4, 오른쪽 자식은 5로 마무리한다.

  • 오른쪽의 경우 3이 첫 번째 값인데, 마침 중위 순회에서는 맨 오른쪽에 위치한다.

    • 이 말은 3의 오른쪽 자식 노드는 존재하지 않는다는 얘기다.

    • 그림에서도 3의 오른쪽 노드가 존재하지 않는 것을 확인할 수 있다.

  • 이제 남아 있는 노드들을 이후에도 계속 분할을 시도하면, 이 그림처럼 트리 형태로 최종적으로 구성할 수 있다.

• 먼저 전위 순회 첫 번째 결과를 가져와 중위 순회를 분할하는 인덱스로 한다.

• 이 값을 현재 노드로 구성하고, 이를 기준으로 중위 순회 결과를 쪼개서 왼쪽, 오른쪽으로 각각 마무리 될 때 분할 정복 구조로 재귀 호출하면, 트리를 구성할 수 있다.

• 여기서 전위 순회 결과는 pop(0)으로 값을 꺼내온다.

  • 파이썬에서는 데크(Deque)로 구현할 수 있다.

  • 여기서는 입력값 리스트를 특별히 다른 자료형으로 변환하지 않고 그대로 사용한다.

  • 파이썬의 리스트는 pop()에도 인덱스를 별도로 지정할 수 있어서, 사실상 스택과 큐의 모든 역할을 수행할 수 있다.

    • 하지만 리스트에서 pop(0)은 시간 복잡도가 O(n)이므로 주의가 필요하다.