- 단어 리스트에서
words[i]+words[j]가 팰린드롬이 되는 모든 인덱스 조합 (i, j)를 구하라.
1. 팰린드롬을 브루트 포스로 계산
class Solution:
def palindromePairs(self, words: List[str]) -> List[List[int]]:
def is_palindrome(word):
return word == word[::-1]
output = []
for i, word1 in enumerate(words):
for j, word2 in enumerate(words):
if i == j:
continue
if is_palindrome(word1 + word2):
output.append([i,j])
return output
-
각각의 모든 조합을 구성해보고 이 구성이 팰린드롬인지 여부를 판별하면, O(n2) 시간 복잡도로 브루트 포스 풀이가 가능할 것 같다.
-
'유효한 팰린드롬' 문제에서 풀어본 풀이 중 가장 간단한 슬라이싱 풀이를 선택한다.
-
이제 n2번 반복하면서 모든 조합을 구성하고, 매번 팰린드롬 여부인지 체크한다.
-
간단하게 구현했고 실행도 잘 된다. 그러나, 리트코드에서는 타임아웃이 발생하며 테스트 케이스를 통과할 수 없다.
2. 트라이 구현
class TrieNode:
def __init__(self):
self.children = collections.defaultdict(TrieNode)
self.word_id = -1
self.palindrome_word_ids = []
class Trie:
def __init__(self):
self.root = TrieNode()
@staticmethod
def is_palindrome(word: str) -> bool:
return word[::] == word[::-1]
# 단어 삽입.
def insert(self, index, word) -> None:
node = self.root
for i, char in enumerate(reversed(word)):
# 두번째 로직에서 문자를 하나씩 제거해가며 팰린드롬을 판별해서 체크함, 여기 word 리스트를 잘라서 체크함 wordreverse 아님!!!!!!!
if self.is_palindrome(word[0:len(word) - i]):
node.palindrome_word_ids.append(index)
node = node.children[char]
node.word_id = index
def search(self, index, word) -> List[List[int]]:
result = []
node = self.root
# 여기 while 에서 node = nod.children[word[0]]으로 node 끝까지 타고 가서 밑에 판별 로직 1, 2에서 끝점이랑 비교가 가능해짐.
while word:
# 판별 로직 3
if node.word_id >= 0:
if self.is_palindrome(word):
result.append([index, node.word_id])
if not word[0] in node.children:
return result
node = node.children[word[0]]
word = word[1:]
"""
판별 로직 1
위쪽 while 문에서 구현된 트라이와 word가 맞을 때 까지 쭉 안으로 들어오고
그 지점에서 if 문이 실행됨.
즉, 꺼꾸로 들어간 트라이와 원래의 word 값이 같은 경우에
밑의 if문으로 걸러짐.
"""
if node.word_id >= 0 and node.word_id != index:
result.append([index, node.word_id])
"""
판별 로직 2
위쪽 while 문에서 구현된 트라이와 word가 맞을 때 까지 쭉 안으로 들어오고
그 지점에서 for 문이 실행됨.
그 자리에 palindrome_word_id가 있으면 그것도 정답.
"""
for palindrome_word_id in node.palindrome_word_ids:
result.append([index, palindrome_word_id])
return result
class Solution:
def palindromePairs(self, words: List[str]) -> List[List[int]]:
trie = Trie()
for i, word in enumerate(words):
trie.insert(i, word)
results = []
for i, word in enumerate(words):
results.extend(trie.search(i, word))
return results
-
일단 전에 구현했던 트라이 구현과 기본적인 뼈대는 동일하다.
-
O(n)으로 풀기 위해서는, 모든 입력값을 트라이로 만들어두고 딱 한 번씩만 탐색하는 문제로 변형할 것이다. 팰린드롬을 판별해야 하기 때문에, 뒤집어서 트라이로 구성하면 해법을 찾을 수 있을 것 같다.
-
['d', 'cbbcd', 'dcbb', 'dcbc' 'cbbc', 'bbcd'] 을 입력값으로 해서 뒤집어서 트라이로 구현해본다.
- 입력값을 뒤집으면 ['d', 'dcbbc', 'bbcd', 'cbcd', 'cbbc', 'dcbb']가 되고 이 값의 트라이를 구축한 결과는 다음과 같다.
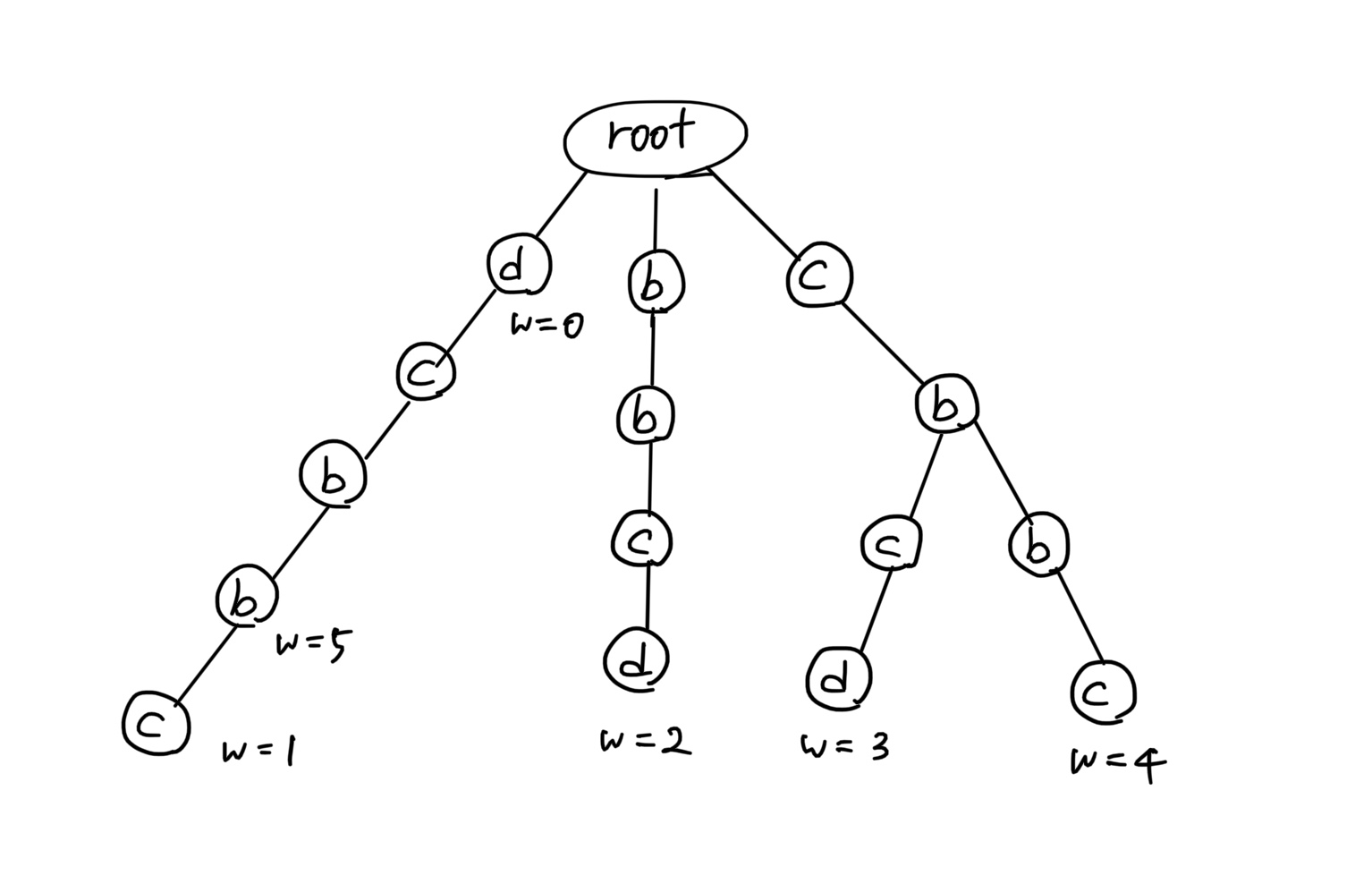
-
뒤집은 다음, 문자 단위로 계속 내려가면서 트라이를 구현하고, 각각의 단어가 끝나는 지범에는 단어 인덱스를
word_id로 부여했다.-
그림에서의
w가 코드에서의word_id이다. -
이전 문제에서는 True, False 여부만 표기했지만, 여기서는 해당 단어의 인덱스를 찾아야 하기 때문에
word_id로 부여했다.
-
1) 단어를 뒤집어서 구축한 트라이이기 때문에 입력값은 순서대로 탐색하다가, 끝나는 지점의 word_id 값이 -1이 아니라면, 현재 인덱스 index와 해당 word_id는 팰린드롬으로 판단할 수 있다.
- 예를 들어 그림에서 입력값 bbcd의 트라이 탐색이 끝나는 지점에서
word_id = 2가 셋팅되어 있고, bbcd의 인덱스는 5이기 때문에, [5, 2]인 bbcd + dcbb는 팰린드롬이며, 이는 정답 중 하나가 된다.
2) 트라이 삽입 중에 남아 있는 단어가 팰린드롬이라면 미리 팰린드롬 여부를 세팅해 두는 방법이다.
-
입력값 ['d', 'dcbbc', 'bbcd', 'cbcd', 'cbbc', 'dcbb']에서 cbbc는 단어 자체가 팰린드롬이므로 루트에 바로 입력값의 인덱스인 p = 4를 셋팅하고,
word[0:len(word) -i]형태로 단어에서 문자 수를 계속 줄여 나가며 팰린드롬 여부를 체크한다. -
문자가 하나만 남게 될 때는 항상 팰린드롬이므로 마찬가지로
p = 4를 마지막에 셋팅한다. -
당연히 이 마지막 값은 항상
w의 바로 앞 노드가 된다. -
팰린드롬 여부인
p를 추가한 트라이는 다음과 같다.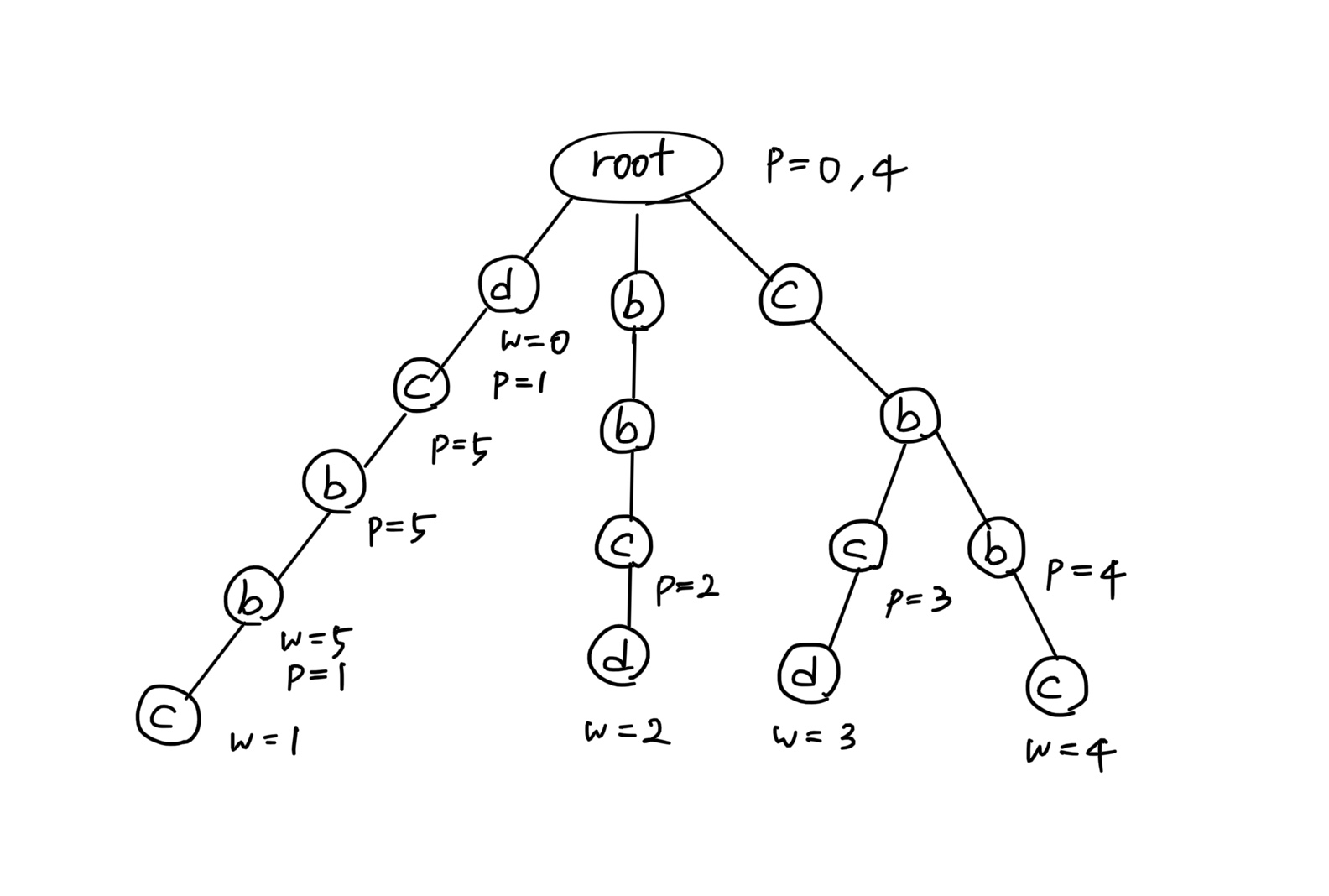
-
삽입 함수를 개선해보자
-
p로 표현한 것을 코드에서는palindrome_word_ids로 풀어서 표현했다. -
속성의 이름을 복수형으로 정했는데, 그 이유는 이 그림의 루트 경우처럼
p값이 여러 개가 될 수 있기 때문이다.
-
-
이제 TrieNode 클래스를 수정한다.
word_id외에도palindrome_word_ids를 트라이 노드의 속성으로 추가하고 TrieNode 클래스로 구현했다.
-
그림에서
w는 단어의 끝이고p는w이전 노드에 반드시 셋팅 된다.
문자가 하나만 남았을 때는 항상 팰린드롬이기 때문이다.-
입력값 ['d', 'dcbbc', 'bbcd', 'cbcd', 'cbbc', 'dcbb']를 보면 dcbb의 인덱스는 2이고, 트라이에서는 d -> c -> b -> b의 마지막 노드가
p = 1이다.-
즉 [0,1]도 정답이 된다.
-
d + cbbcd이며 마찬가지로 팰린드롬이다.
-
-
3) 입력값을 문자 단위로 확인해 나가다가 해당 노드의 word_id가 -1이 아닐 때, 나머지 문자가 팰린드롬이라면 팰린드롬으로 판별하는 경우다.
-
dcbc + d가 이에 해당하는데, 입력값 dcbc는 먼저 d부터 탐색하다가 d의
word_id가-1이 아니기 때문에 나머지 문자 cbc에 대한 팰린드롬 여부를 검사한다.- 여기서는 dcbc + d를 팰린드롬으로 판별한다.
<3가지 판별 로직 정리>
-
끝까지 탐색했을 때
word_id가 있는 경우 -
끝까지 탐색했을 때
palindrome_word_ids가 있는 경우 -
탐색 중간에
word_id가 있고, 나머지 문자가 팰린드롬인 경우
