64. K Closest Points to Origin

리트코드

• 평면상에 points 목록이 있을 때, 원점 (0, 0)에서 K번 가까운 점 목록을 순서대로 출력하라.

  • 평면상 두 점의 거리는 유클리드 거리로 한다.

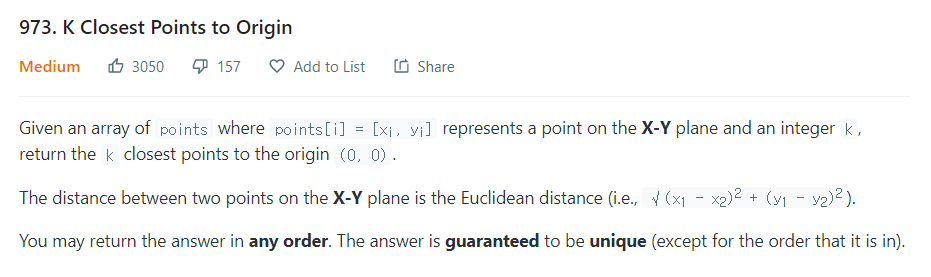
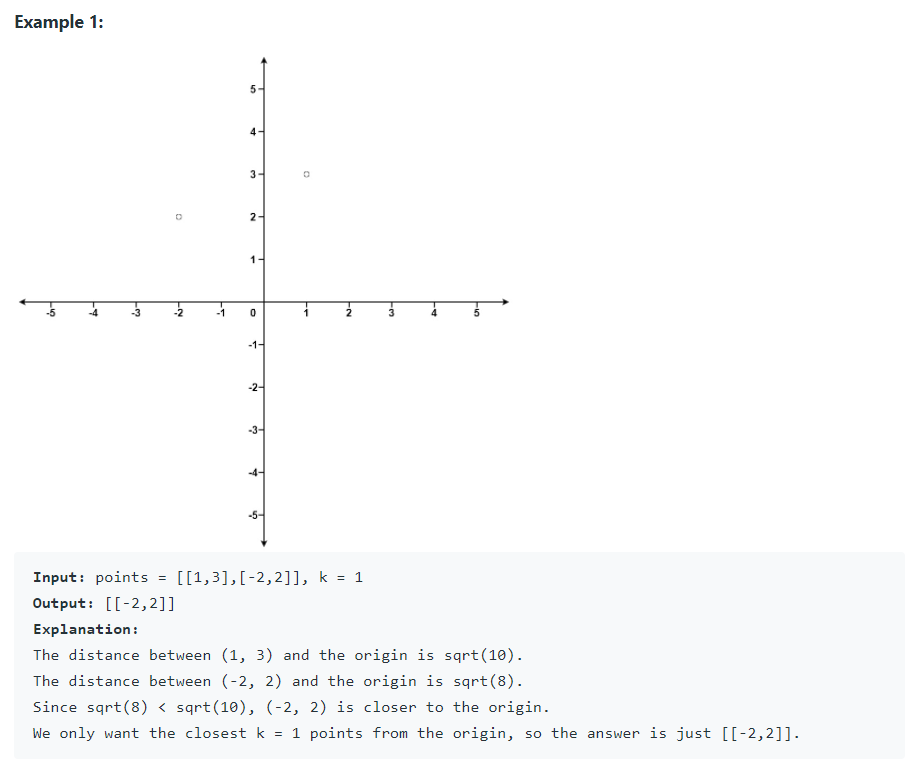
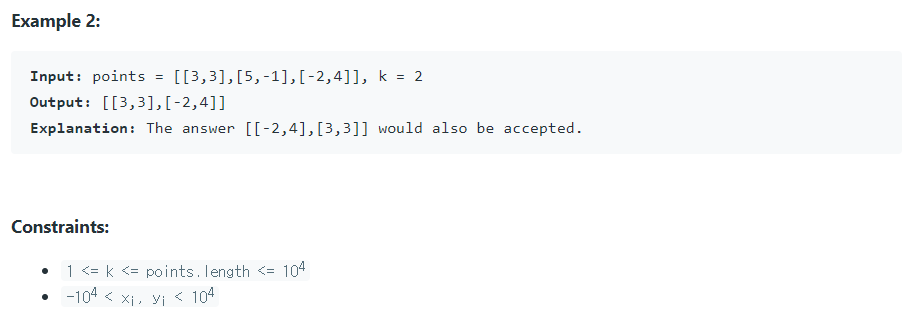
유클리드 거리의 우선순위 큐 순서

class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        heap = []
        for (x, y) in points:
            dist = x ** 2 + y ** 2
            heapq.heappush(heap, (dist, x, y))
            
        result = []
        for _ in range(k):
            (dist, x, y) = heapq.heappop(heap)
            result.append((x, y))
        return result
            
        
        

• 유클리드 거리(Euclidean Distance)는 유클리드 공간에서 두 점 사이의 거리를 계산하는 가장 '일반적인' 방법 중 하나로 수식은 다음과 같다.

  

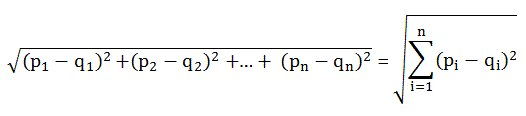
• 예를 들어 원점 (0, 0)을 x 좌표라고 할 때 (1, 3)에 있는 y 좌표와의 유클리드 거리는 √(0-1)2 + (0-3)2 이고 이 값은 √10, 약 3.16 정도가 된다.

  • 이 값을 크기가 작은 순으로 k번 추출하면 되는 어렵지 않게 풀 수 있는 문제다.

• k번 추출이라는 단어에서 바로 우선순위 큐를 떠올릴 수 있다.

  • 유클리드 거리를 계산하고 이 값을 우선순위 큐로 k번 출력하면 쉽게 문제를 풀이할 수 있다.

• math 모듈을 사용해 위의 유클리드 거리 수식을 구현해 계산하고 힙에 삽입한다.

  • 파이썬의 heapq 모듈은 최소 힙이기 때문에 거리가 가까운 순을 출력해야 하는 이 문제 풀이에 더욱 적합하다.

    • 만약 가장 먼 거리를 출력해야 한다면, 음수로 변환하여 -dist를 삽입하는 형태로 풀이할 수 있을 것이다.

• 이제 결과를 추출할 차례다.

  • 결과 리스트에 힙에서 추출한 결과를 k번 삽입해 리턴하면 된다.

class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        heap = []
        for (x, y) in points:
            dist = math.sqrt((0-x) ** 2 + (0-y) ** 2)
            heapq.heappush(heap, (dist, x, y))
            
        result = []
        for _ in range(k):
            (dist, x, y) = heapq.heappop(heap)
            result.append((x, y))
        return result

• 그런데 여기서 거리를 계산해 다른 데서 활용할 게 아니라면 수식을 좀 더 갈략하게 만들 수 있을 것 같다.

  • 어차피 순서만 동일하면 되기 때문이다.

  • 따라서 여기서 math.sqrt()는 생략해도 무방하다.

  • 이 경우 불필요한 계산을 줄일 수 있으므로 수행 속도를 더욱 높일 수 있다.