65. Binary Search

리트코드

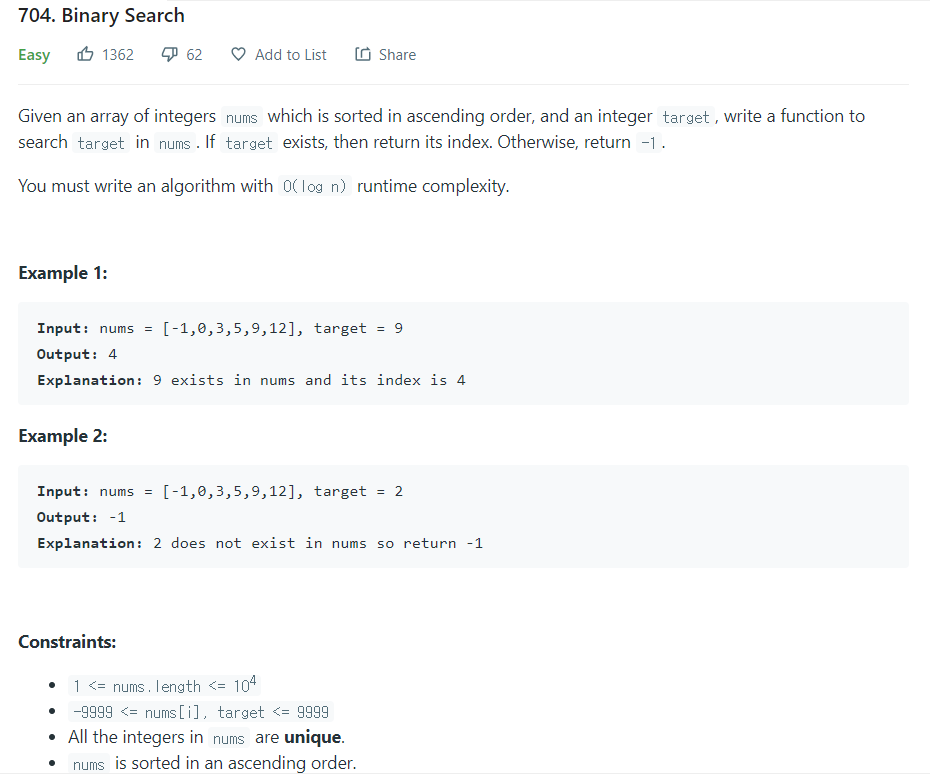
• 정렬된 nums를 입력받아 이진 검색으로 target에 해당하는 인덱스를 찾아라.

1. 재귀 풀이

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        def binary_search(left, right):
            if left <= right:
                mid = (left + right) // 2
                #버그 개선은 다음과 같이 (자료형 최댓값)
                # mid = left + (right - left) // 2
                
                if nums[mid] < target:
                    return binary_search(mid + 1, right)
                elif nums[mid] > target:
                    return binary_search(left, mid - 1)
                else:
                    return mid
                
            else: return -1
            
        return binary_search(0, len(nums) - 1)
        

• 먼저 간단히 재귀로 이진 검색을 구현할 수 있다.

• 절반씩 범위를 줄여나가며 맞출 때까지 계속 재귀 호출하면 된다.

  • 카드 마술 설명과 동일한 정석대로의 풀이다.

2. 반복 풀이

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        while left <= right:
            mid = (left + right) // 2
            
            if nums[mid] < target:
                left = mid + 1
            elif nums[mid] > target:
                right = mid - 1
            else:
                return mid
            
        return -1

• 대개는 재귀 풀이가 더 우아한 편이지만, 반복 풀이는 좀 더 직관적이라 이해가 쉽다는 장점이 있다.

3. 이진 검색 모듈

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        index = bisect.bisect_left(nums, target)
        
        if index < len(nums) and nums[index] == target:
            return index
        else:
            return -1

• 앞의 풀이에서는 이진 검색을 직접 구현했지만, 파이썬에서는 이진 검색을 직접 구현할 필요가 없다.

  • 이진 검색 알고리즘을 지원하는 bisect 모듈을 기본으로 제공하기 때문이다.

  • 여러가지 예외 처리를 포함한 이진 검색 알고리즘이 깔끔하게 모듈 형태로 구현되어 있다.

• bisect 모듈을 사용해서 이진 검색을 파이썬다운 방식으로 풀이할 수 있다.

4. 이진 검색을 사용하지 않는 index 풀이 (272ms)

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        try:
            return nums.index(target)
        except ValueError:
            return -1

• 파이썬에서 제공하는, 해당 값의 인덱스를 찾아내는 index() 메소드를 활용하는 방법이다.

• 이 경우 존재하지 않는 값이라면 에러가 발생하므로, 에러인 ValueError를 예외 처리하여 -1을 리턴하도록 처리하면 풀이가 가능하다.

• 이 방식은 이진 검색이 아니며, 이진 검색을 요구하는데 이렇게 풀이해선 안된다.

➕ 이진 검색 풀이와 index()를 이용한 풀이

입력값 [-1, 0, 3, 5, 9, 12]을 기준으로 속도 테스트를 진행해보자.

index()쪽은 179ns인 데 반해 이진 검색 모듈은 273ns로 오히려 index()가 30% 이상 빠르다.

이번에는 입력값을 좀 더 크게 해보자.

a = [i for i in range(1, 100000, 3)]

• 1부터 100000까지 3칸씩 건너뛰는 큰 배열을 생성했다.

이제 세 번째 값인 7을 찾는 성능 테스트를 진행해보자.

이번에도 index()가 201ns로 이진 검색 모듈의 561ns에 비해 2배 이상 빠르다.

중후반부에 위치한 77500을 찾으니 놀라운 일이 발생했다.

이진 검색은 618ns로, 앞서 7을 찾던 것과 거의 속도 차이가 없으나, index()의 경우 331ms로 무려 1,000배 이상 느려졌다.

• 앞에서부터 차례대로 찾는 index()함수는 최악의 경우 O(n)으로, 뒤에 위치한 값일수록 점점 찾는 속도가 느려지며 이처럼 1,000배나 가까이 차이 나는 경우도 있다.

• 이진 검색은 항상 일정한 속도를 보인다. 이진 검색은 O(logn)으로, 아무리 큰 값이라도 속도 차이가 거의 없다.

  • 로그의 마법 때문이다.

• bisect모듈은 원래 리스트의 삽입 지점을 찾는 모듈이지만 이처럼 이진 검색으로 위치를 찾는 데에도 매우 유용하다.