67. Intersection of Two Arrays

리트코드

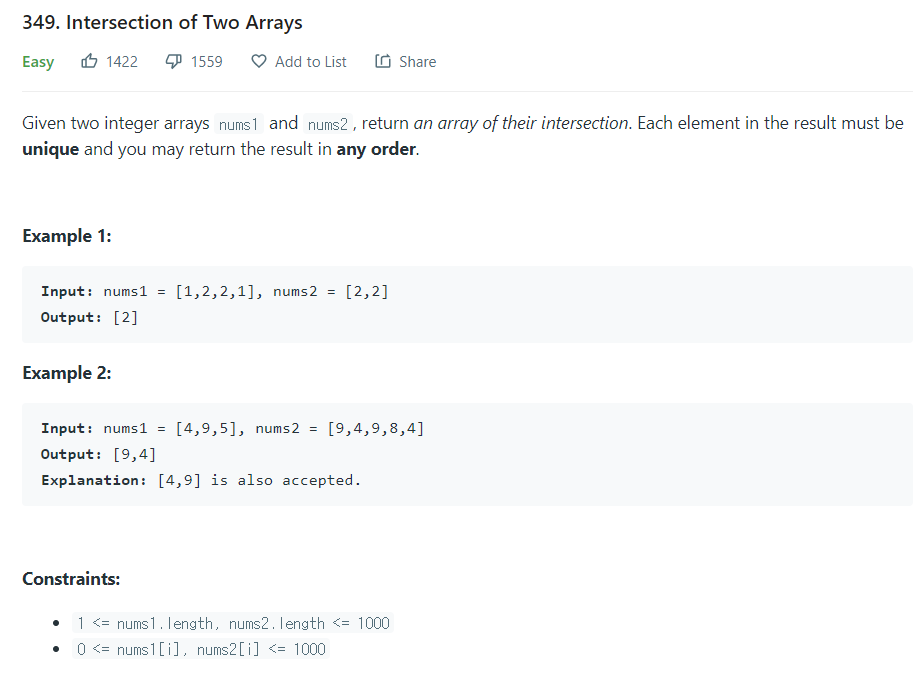
• 두 배열의 교집합을 구하라.

1. 브루트 포스로 계산

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        result: Set = set()
        for n1 in nums1:
            for n2 in nums2:
                if n1 == n2:
                    result.add(n1)
                    
        return result
    

• 먼저 가장 간단하고 직관적인 브루트 포스로 풀어본다.

• O(n2)으로 반복하면서 일치하는 경우 무조건 추가한다.

  • 데이터 타입은 집합이기 때문에 속도는 느리긴해도 중복된 값은 알아서 잘 처리해줄 것이다.

2. 이진 검색으로 일치 여부 판별

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        result: Set = set()
        nums2.sort()
        
        for n1 in nums1:
            #이진 검색으로 일치 여부 판별
            i2 = bisect.bisect_left(nums2, n1)
            if len(nums2) > 0 and len(nums2) > i2 and n1 == nums2[i2]:
                result.add(n1)
                
        return result

• bisect_left에 대해서는 다음 블로그를 참고하자.

• 한쪽은 순서대로 탐색하고 다른 쪽은 정렬해서 이진 검색으로 값을 찾으면, 검색 효율을 획기적으로 높일 수 있다.

  • 이 경우 시간 복잡도는 O(nlogn)이 될 것이다.

• nums2는 정렬한 상태에서, nums1을 O(n) 순차 반복하면서 nums를 O(logn) 이진 검색한다.

• 최초 정렬에 소요되는 O(nlogn) 을 감안해도 전체 O(nlogn) 에 가능하므로 앞서 O(n2) 에 비해 훨씬 좋은 성능을 보인다.

3. 투 포인터로 일치 여부 판별

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        result: Set = set()
            
        #양쪽 모두 정렬
        nums1.sort()
        nums2.sort()
        i = j = 0
        
        #투 포인터 우측으로 이동하며 일치 여부 판별
        while i < len(nums1) and j < len(nums2):
            if nums1[i] > nums2[j]:
                j += 1
            elif nums1[i] < nums2[j]:
                i += 1
                
            else:
                result.add(nums1[i])
                i += 1
                j += 1
                
        return result
    

• 이 문제는 양쪽 다 정렬하여 투 포인터로 풀이할 수도 있다.

  • 마치 병합 정렬 시 마지막에 최종 결과를 비교하는 과정과 유사하다.

    • 다만 일치하는 값을 판별한다는 차이만 있을 뿐이다.

• 정렬에 2*O(nlogn), 비교에 O(2n) 이 소요되므로, 마찬가리로 전체 O(nlogn)에 풀이가 가능하다.