68. Two Sum II - Input array is sorted

리트코드

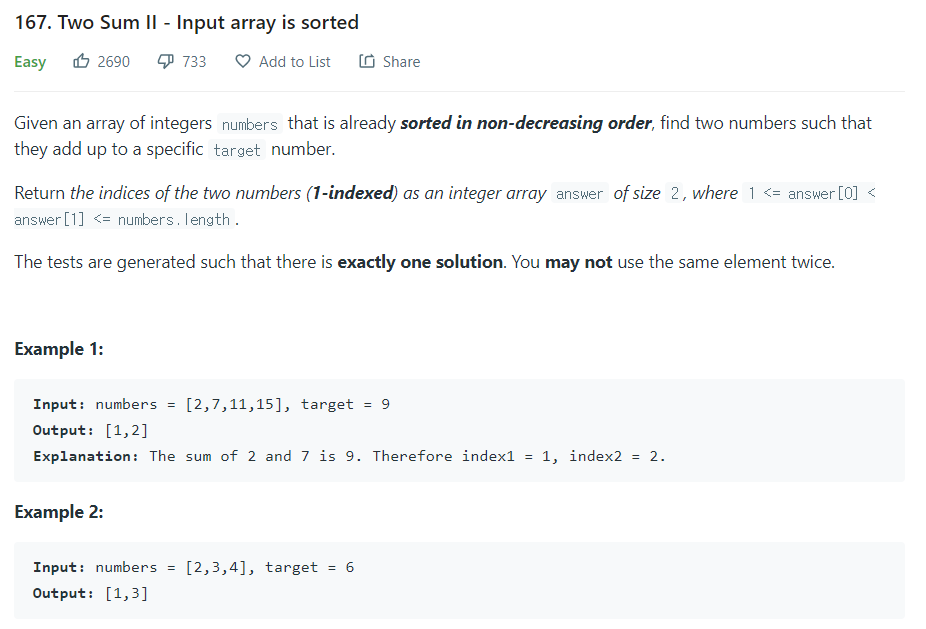
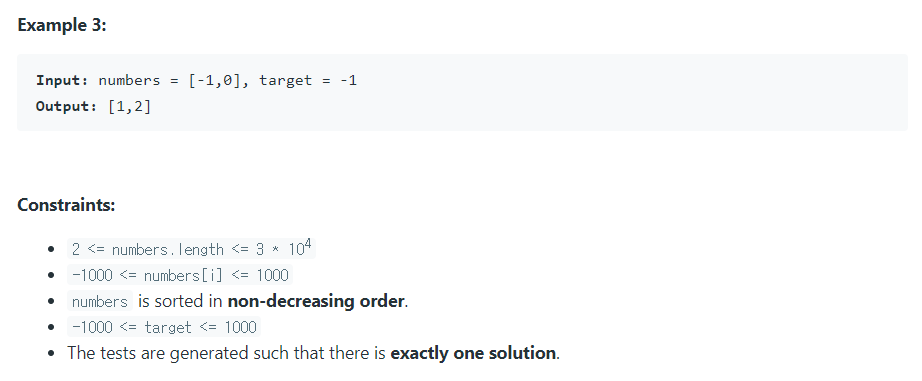
• 정렬된 배열을 받아 덧셈하여 타겟을 만들 수 있는 배열의 두 숫자 인덱스를 리턴하라.

  • 주의: 이 문제에서 배열은 0(Zero-Based)이 아닌 1부터 시작하는 것으로 한다.

1. 투 포인터

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        left, right = 0, len(numbers) - 1
        while not left == right:
            if numbers[left] + numbers[right] < target:
                left += 1
            elif numbers[left] + numbers[right] > target:
                right -= 1
            else:
                return left + 1, right + 1 #리턴 값  +1

• 7번 '두 수의 합' 문제는 투 포인터로 풀 수 없다고 했으나, 그 문제의 다른 버전 격인 이 문제는 입력 배열이 정렬되어 있다는 가정이 추가됐다.

  • 따라서 이 문제는 투 포인터로도 잘 풀릴 것이다.

• 7번 문제의 코드의 일부를 가져온다.

  • 이 문제의 경우 특별히 0이 아닌 1부터 시작한다고 했으니, 리턴하는 부분의 값에 각각 +1을 한다.

  • 문제에서 입력값에 해당하는 변수명이 기존 nums에서 numbers로 바뀌었으미 이부분만 수정해주면 문제없이 잘 풀릴 것 같다.

• 투 포인터 풀이의 경우, O(n)에 풀이할 수 있다.

2. 이진 검색

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        for k, v in enumerate(numbers):
            left, right = k + 1, len(numbers) - 1
            expected = target - v
            
            #이진 검색으로 나머지 값 판별
            while left <= right:
                mid = left + (right - left) // 2
                if numbers[mid] < expected:
                    left = mid + 1
                elif numbers[mid] > expected:
                    right = mid - 1
                else:
                    return k + 1, mid + 1

• 현재 값을 기준으로 나머지 값이 맞는지 확인하는 형태의 이진 검색 풀이를 시도해볼 수 있을 것 같다.

• 이 경우 이진 검색 logn을 n번 반복하므로 시간 복잡도는 O(nlogn)이 된다.

• 이진 검색 풀이가 투 포인터에 비해 2배 가향 늦다.

  • 그렇다면 bisect모듈을 사용하면 속도를 더 높일 수 있을까?

3. bisect 모듈 + 슬라이싱

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        for k, v in enumerate(numbers):
            left, right = k + 1, len(numbers) - 1
            expected = target - v
            
            i = bisect.bisect_left(numbers[k + 1:], expected)
            if i < len(numbers[k + 1:]) and numbers[i + k + 1] == expected:
                return k + 1, i + k + 2
                
                

• left와 right 변수도 필요 없고, 예상대로 코드는 엄청나게 깔끔해졌다.

  • 그런데 문제가 있다. 이 풀이 속도는 무려 2184ms에 다다른다.

4. bisect 모듈 + 슬라이싱 최소화

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        for k, v in enumerate(numbers):
            left, right = k + 1, len(numbers) - 1
            expected = target - v
            
            i = bisect.bisect_left(numbers[k + 1:], expected)
            if i < len(numbers[k + 1:]) and numbers[i + k + 1] == expected:
                return k + 1, i + k + 2

• 파이썬 슬라이싱을 무리하게 적용한 게 원인인 듯 하여 nums 변수에 한 번만 사용해 담아두는 형태로 개선을 시도했다.

• 이렇게 하니 1136ms로 앞서 풀이에 비해 2배가량 빨라졌다.

  • 그래도 투포인터에 비하면 많이 느리다. 조금 더 개선이 필요하다.

5. bisect 모듈 + 슬라이싱 제거

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        for k, v in enumerate(numbers):
            left, right = k + 1, len(numbers) - 1
            expected = target - v
            
            i = bisect.bisect_left(numbers[k + 1:], expected, k + 1)
            if i < len(numbers) and numbers[i] == expected:
                return k + 1, i + 1

• bisect 모듈의 기능을 좀 더 활용하기로 한다.

  • 기본 파라미터 외에도 여러 추가 파라미터가 있다.

bisect.bisect_left(a, x, lo = 0, hi = len(a))

• 이를 참고하여 왼쪽 범위를 제한하는 파라미터인 lo를 찾아냈고, 이 값을 지정하는 것으로 풀이를 진행했다.

  • 더 이상 슬라이싱을 사용할 필요가 없어졌다.

• 이 경우 68ms로 , 투 포인터 풀이와 속도가 같아졌다.

  • 슬라이싱을 사용하지 않고도 bisect 모듈만을 이용해 이진 검색의 성능을 개선하는 데 비로소 성공했다.

  • 슬라이싱은 편리하고 빠른 모듈이지만, 이처럼 생각 없이 무분별하게 남용하다보면 속도 저하의 주범이 될 수 잇다.

    • 경우에 따라서는, 꼭 필요한 곳에만 적절히 사용해야 실행 속도를 좀 더 최적화할 수 있다.

➕ 파이썬의 슬라이싱은 매우 효율적이고 빠르다고 했는데 왜 이런 일이 발생할까?

그 이유는 슬라이싱은 매번 새롭게 객체를 생성해서 할당하게 되고, 엄청나게 큰 배열의 경우 슬라이싱으로 새로운 객체를 생성하는 데 상당한 시간이 들기 때문이다.

배열의 길이를 계산하는 데도 매번 길이를 계산ㄴ하는 비용이 들기 때문에, 여기서 상당한 시간이 소요된다.