69. Search a 2D Matrix II

리트코드

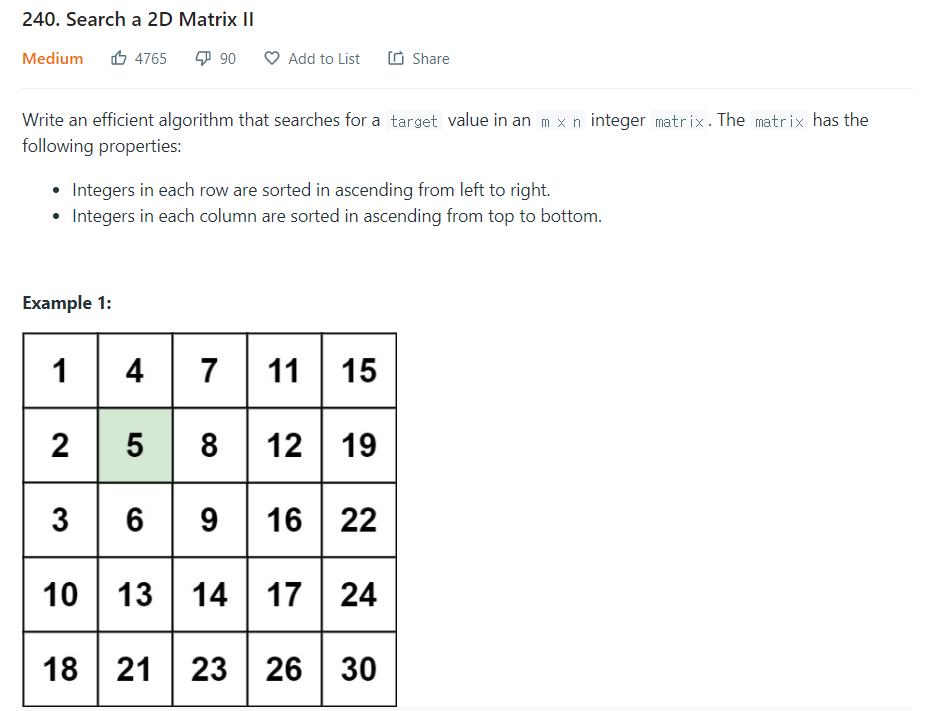
• m x n 행렬에서 값을 찾아내는 효율적인 알고리즘을 구현하라.

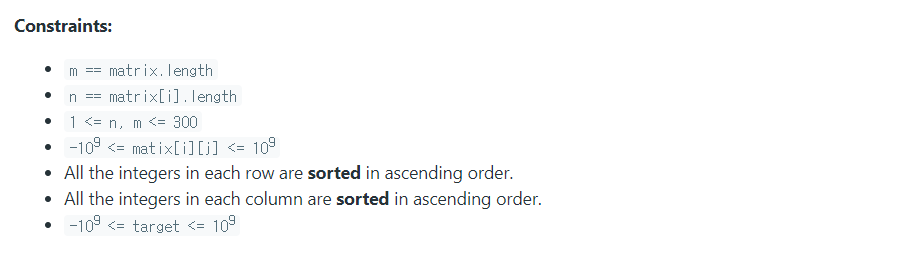
  • 행렬은 왼쪽에서 오른쪽, 위에서 아래 오름차순으로 정렬되어 있다.

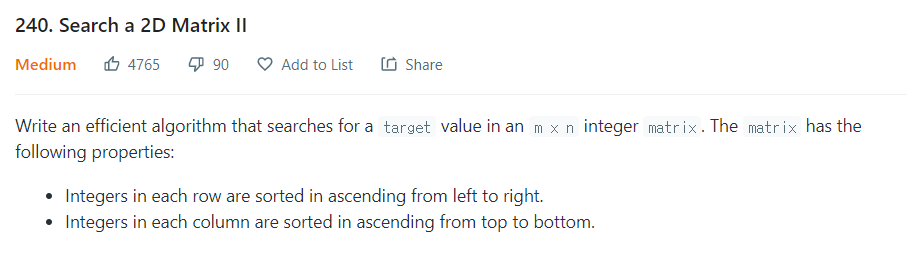
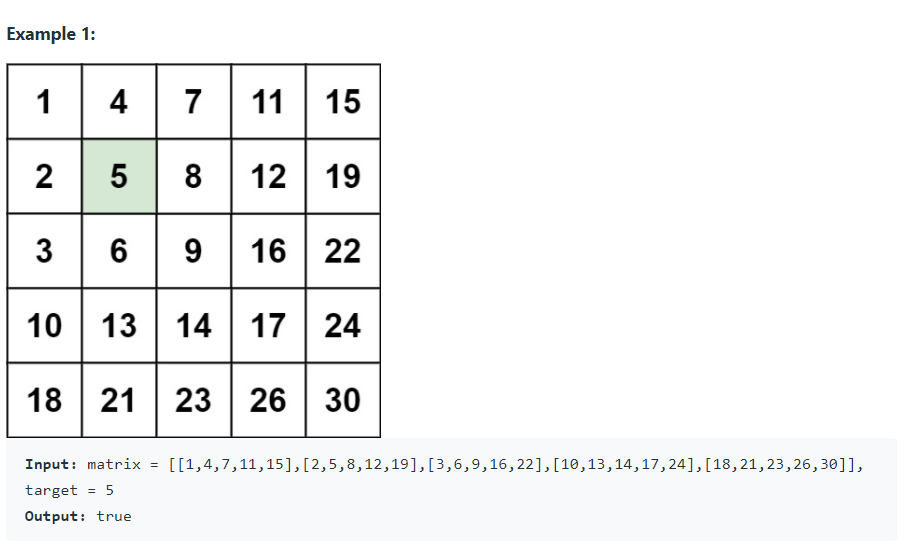
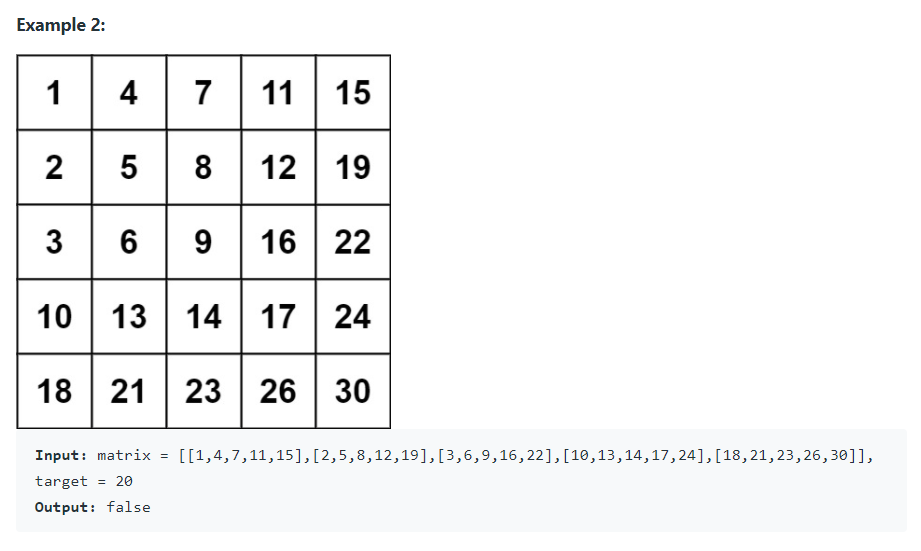
1. 첫 행의 맨 뒤에서 탐색 (36ms)

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        #예외 처리
        
        if not matrix:
            return False
        
        #첫 행의 맨 뒤
        row = 0
        col = len(matrix[0] - 1)
        
        while row <= len(matrix) - 1 and col >= 0:
            if target == matrix[row][col]:
                return True
            #타겟이 작으면 왼쪽으로 이동
            elif target < matrix[row][col]:
                col -= 1
            #타겟이 크면 아래로 이동
            elif target > matrix[row][col]:
                row += 1
        return False
    
    

• 이 문제는 행을 기준으로 이진 검색을 수행한 다음, 찾아낸 값을 기준으로 해당 위치의 각 열을 기준으로 다시 이진 검색을 수행하면 해결할 수 있을 것 같다.

  • 첫 번째 이진 검색은 쉽게 할 수 있지만, 두 번째 이진 검색은 생각보다 효율적으로 풀이하기가 쉽지 않다.

  • 왜냐하면 각 행에서 특정 인덱스를 기준으로 값을 추출해오는데 적지 않은 연산이 필요하기 때문이다.

• 예를 들어, 각 행의 세 번째 인덱스를 가져온다고 해보자.

  • 이 경우 matrix[n][3]과 같이 각 행에 대한 값 추출 작업이 필요하므로 결국 O(n) 이 필요하며, 이진 검색으로 인한 O(logn)의 성능을 누릴 수 없다.

  • 첫 번째 행을 찾아낸다 해도 그게 정확한지 확신할 수 없다. 얼마든지 다른 행에 정답이 있을 수 있기 때문이다.

• 여기서는 좀 더 단순한 방법을 사용해보자.

  • 첫 행의 맨 뒤 요소를 택한 다음, 타겟이 이보다 작으면 왼쪽으로, 크면 아래로 이동하게 하는 방법이다.

  • 행렬은 왼쪽에서 오른쪽, 위에서 아래로 오름차순으로 정렬되어 있기 때문에, 작으면 왼쪽, 크면 아래로 이동하면 원하는 위치에 어렵지 않게 도달할 수 있을 것이다.

2. 파이썬다운 방식 (36ms)

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        return any(target in row for row in matrix)
    
    

• 앞서 풀이는 뒤에서부터 한 칸씩 왼쪽, 아래쪽으로 움직이며 탐색하는 방식이었으나, 이 경우에는 파이썬이 내부적으로 행렬에 값이 존재하는지 여부를 위에서부터 차례대로 한 줄씩 탐색하게 될 것이다.

➕

any()라는 함수는 포함된 값 중 어느 하나가 참이라면 항상 참으로 출력한다.

논리연산의 OR과 유사하다.

all() 이라는 함수도 있는데, 이 함수는 모든 값이 참이어야 True를 출력한다.

논리연산의 AND와 유사하다.

• 아이러니 하게도 이 문제는 이진 검색으로 풀이가 어렵고, 조금 다른 방법을 사용해야 했다.

  • 예상과 달리 다른 방법으로 풀리는 경우가 있으므로, 실제 코딩 테스트 시에도 예상방식대로 풀이가 되지 않는다면 그 방식에 너무 많은 시간을 허비하지 않도록 유의해야 한다.