85. Fibonacci Number

리트코드

• 피보나치 수를 구하라.

1. 재귀 구조 브루트 포스 (888ms)

class Solution:
    def fib(self, n: int) -> int:
        if n <= 1:
            return n
        return self.fib(n - 1) + self.fib(n - 2)

• 브루트 포스로는 안 풀릴 것 같지만 이렇게 기본적이 낭ㄹ고리즘으로도 풀리긴 한다.

  • 이제 다른 방식으로 최적화를 진행해보자.

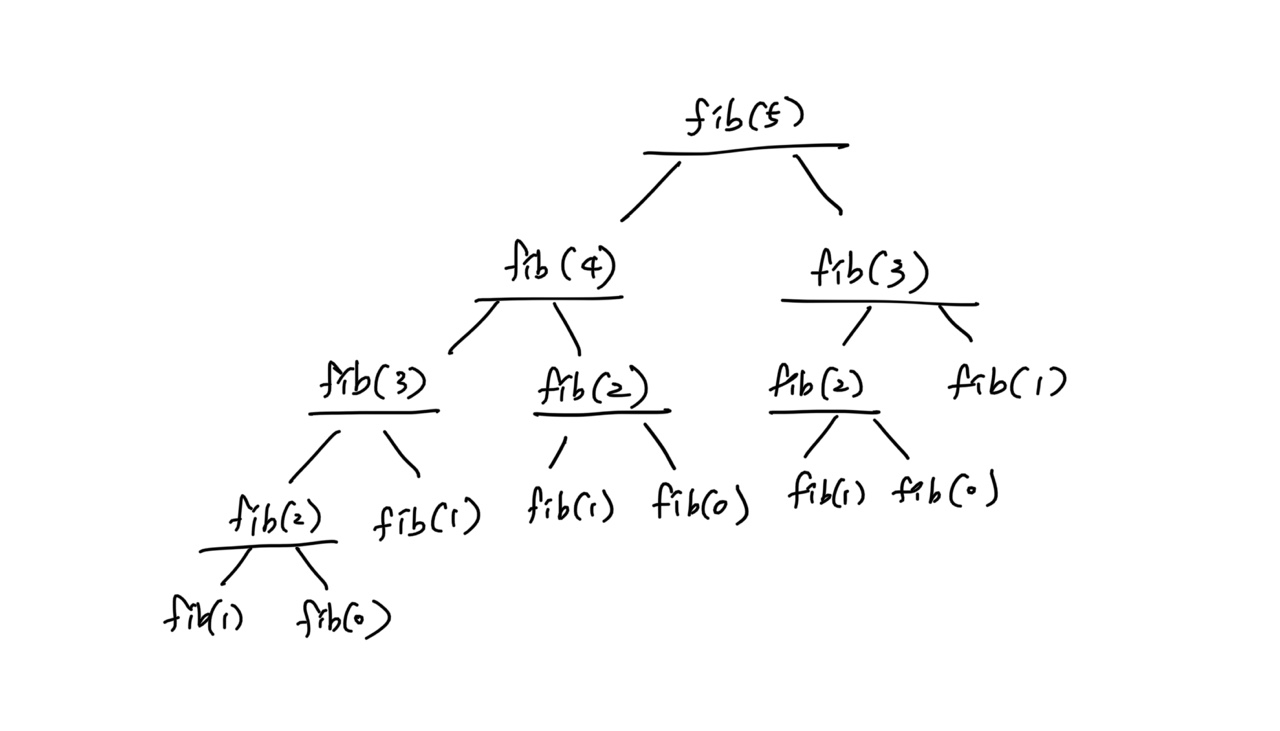
<피보나치 수 재귀 구현 계산 트리>

2. 메모이제이션 - 하향식 (28ms)

class Solution:
    dp = collections.defaultdict(int)
    def fib(self, n: int) -> int:
        if n <= 1:
            return n
        
        if self.dp[n]:
            return self.df[n]
        
        self.dp[n] = self.fib(n-1) + self.fib(n-2)
        return self.dp[n]
        
        

• 다이나믹 프로그래밍의 하향식 풀이로 정리한 것이 바로 이 문제의 메모이제이션 풀이다.

• 원래의 브루트 포스 풀이와 유사하게 재귀로 계산해 나가지만, 이미 계산한 값은 저장해뒀다가 바로 리턴한다.

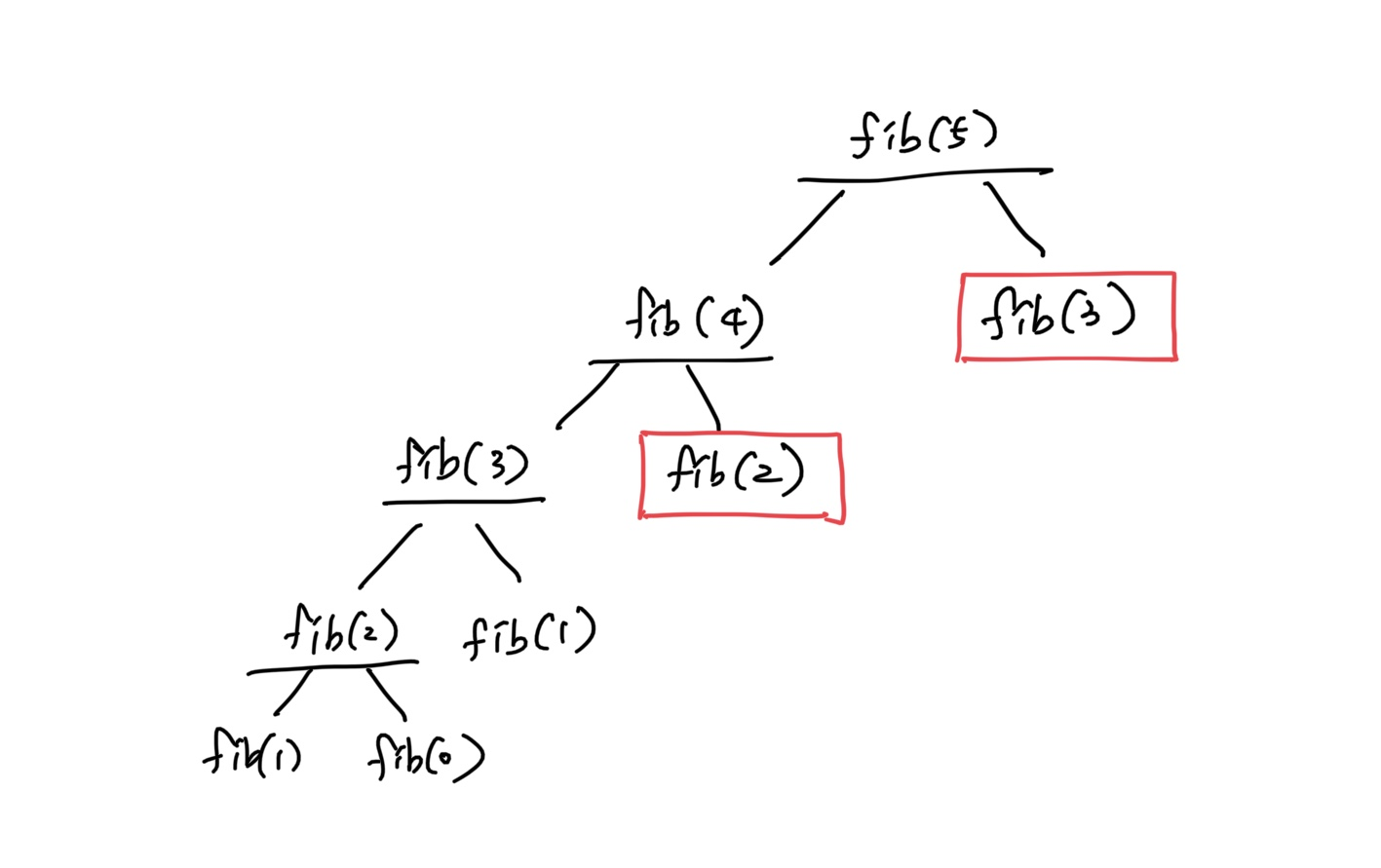
  • fib(5)일 때, 15번 연산을 진행하던 구조는 메모이젣이션 풀이에서는 9번의 연산만으로 풀이할 수 있게 된다.

  • 한 번 계산한 수는 더 이상 계산하지 않으므로 fib(2)와 fib(3)은 한 번만 계산하게 되어 매우 효율적이다.

<피보나치 수 메모이제이션 계산 트리>

3. 타뷸레이션 - 상향식 (24ms)

class Solution:
    dp = collections.defaultdict(int)
    def fib(self, n: int) -> int:
        self.dp[1] = 1
        
        for i in range(2, n + 1):
            self.dp[i] = self.dp[i - 1] + self.dp[i - 2]
        return self.dp[n]
        

• 상향식 풀이, 즉 타뷸레이션 방식으로 풀이한 코드를 살펴보자.

• 재귀를 사용하지 않고 반복으로 풀이하며, 작은 값부터 직접 계산한며서 타뷸레이션한다.

  • 미리 계산을 해두는 것인데, 다른 복잡한 다이나믹 프로그래밍 문제와는 달리 타뷸레이션이 일차원 선형구조라 복잡하지 않고, 구조 자체도 단순해 이해가 수운 편이다.

4. 두 변수만 이용해 공간 절약 (24ms)

class Solution:
    def fib(self, n: int) -> int:
        x, y = 0, 1
        for i in range(0, n):
            x, y = y, x + y
        return x

• 앞서 풀이는 dp라는 딕셔너리에 결과를 차곡차곡 담아 나갔지만 변수는 2개만 있어도 충분하다.

  • 여기서는 편의상 그대로 사용했지만, 사실 단순 배열만 사용해도 충분하다.

• 이 경우 앞서 풀이처럼 메소드 바깥에 클래스의 멤버 변수도 선언할 필요가 없기 때문에 코드는 훨씬 더 간결해진다.

  • 공간 복잡도도 O(n)에서 O(1)로 줄어든다.